何かあれば GitHub のリポジトリに issue を作るか ryukau@gmail.com までお気軽にどうぞ。

インデックスに戻る

Update: 2024-08-06

Table of Contents

トゥルーピーク (true-peak) は離散信号のサンプル間を考慮したピーク値のことで、インターサンプルピーク (inter-sample peak) と呼ばれることもあります。

トゥルーピークという言葉を使っている資料としては ITU-R BS.1770 がありますが、はっきりとした定義は書いていません。そこで、この文章ではトゥルーピークを以下のように定義します。

離散信号を sinc 補間して得られる、連続な信号の絶対値の最大値。

ここではトゥルーピークの計算に適当なフィルタとそのパラメータを調べています。また、理論上の最悪の場合にトゥルーピークの真値と近似値がどれくらい異なるのかを調べています。

Sinc 補間を使えば、一定の間隔でサンプリングされた離散信号から、帯域制限された連続な信号を復元できます。帯域制限された信号とは、連続系から離散系に変換したときにエイリアシングノイズが出ない信号のことです。

以下は Sinc 補間の式です。

\[ \begin{aligned} x(t) &= \sum_{n=-\infty}^{\infty} x[n] \mathrm{sinc} \left( t - n \right)\\ \mathrm{sinc}(x) &= \frac{\sin(\pi x)}{\pi x} \end{aligned} \]

Sinc 補間は \(\mathrm{sinc}(t-n)\) を無限の長さに渡って畳み込む FIR フィルタです。現実には無限の長さのフィルタは計算できないので、録音した信号の範囲外を 0 と仮定して計算します。ここでは入力信号 \(x\) の 2 倍の長さのフィルタ係数を用意して、 scipy.signal.convolve で畳み込んでいます。

Sinc 補間はトゥルーピークを求めたい信号が全て録音された後でないと計算できないので、リアルタイムでは使えません。そこで、精度は下がるものの素早く計算できる分数ディレイフィルタ (fractional delay filter) を使います。例えば ITU-R BS.1770-4 の Annex 2 にはトゥルーピークを計算する FIR の分数ディレイフィルタが掲載されています。

分数ディレイフィルタはサンプル間の値を計算するように設計されたフィルタのことです。大まかに以下のような特徴があります。

より詳しくは以下の資料が参考になります。

ここでは以下の分数ディレイフィルタを比較します。

ラグランジュ補間と Thiran オールパスフィルタは次数を変えることで精度と計算速度のバランスを調節できます。 SOCP FIR は以下の 4 つのパラメータがあります。

遅延は [delta_min, delta_min + 1] サンプルの範囲で設定されます。例えば delta_min=5.0 かつ、オーバーサンプリングが 4 倍のときは [5.0, 5.25, 5.5, 5.75, 6.0] の 5 つのフィルタを組にして設計します。

SOCP FIR の計算方法は以下のリンク先に掲載しています。上で紹介した SOCP FIR のパラメータ名はリンク先のコードに基づいています。

ラグランジュ補間の計算方法は以下のリンク先に掲載しています。

Thiran オールパスフィルタと BS.1770 FIR については、ここで簡単に紹介します。

Thiran オールパスフィルタは IIR の分数ディレイフィルタです。

次の式は \(N\) 次の離散オールパスフィルタの伝達関数です。

\[ H(z) = \frac{ a_N + a_{(N-1)} z^{-1} + \dots + a_1 z^{-(N-1)} + z^{-N} }{ 1 + a_1 z^{-1} + \dots + a_{N-1} z^{-(N-1)} + a_N z^{-N} } \]

Thiran オールパスフィルタでは以下の式によって \(a_1, \dots , a_N\) の値を決めます。

\[ a_k = (-1)^k \binom{N}{k} \prod_{n=0}^{N} \frac{D - N + n}{D - N + k + n} \]

\(k\) は \(1\) から \(N\) の範囲のインデックスです。

\(D\) は分数ディレイのサンプル数で、 \((N, N + 1)\) の範囲で指定するといいそうです。例えば 16 次で 0.1 サンプルの分数ディレイが欲しいときは \(D = 16.1\) とします。

\(D = N - k\) のときに 0 除算が起こります。 \(D \bmod 1 \neq 0\) となるように \(D\) を設定すると 0 除算を避けられます。

BS.1770 FIR は ITR-R BS.1770-4 の Annex 2 に掲載されている FIR の分数ディレイフィルタです。以下は JSON 形式にしたフィルタ係数です。

{
  "Phase 0": [
    0.001708984375, 0.010986328125, -0.0196533203125, 0.033203125,
    -0.0594482421875, 0.1373291015625, 0.97216796875, -0.102294921875,
    0.047607421875, -0.026611328125, 0.014892578125, -0.00830078125
  ],
  "Phase 1": [
    -0.0291748046875, 0.029296875, -0.0517578125, 0.089111328125,
    -0.16650390625, 0.465087890625, 0.77978515625, -0.2003173828125,
    0.1015625, -0.0582275390625, 0.0330810546875, -0.0189208984375
  ],
  "Phase 2": [
    -0.0189208984375, 0.0330810546875, -0.0582275390625, 0.1015625,
    -0.2003173828125, 0.77978515625, 0.465087890625, -0.16650390625,
    0.089111328125, -0.0517578125, 0.029296875, -0.0291748046875
  ],
  "Phase 3": [
    -0.00830078125, 0.014892578125, -0.026611328125, 0.047607421875,
    -0.102294921875, 0.97216796875, 0.1373291015625, -0.0594482421875,
    0.033203125, -0.0196533203125, 0.010986328125, 0.001708984375
  ]
}

Phase 0 の配列の前後を逆にすると Phase 3 、 Phase 1 の配列の前後を逆にすると Phase 2 と係数が同じになります。

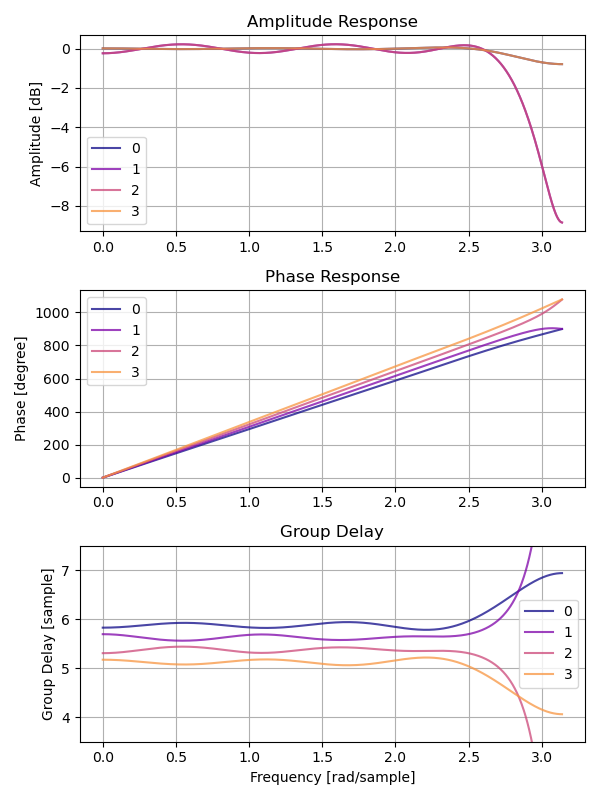
BS.1770 FIR の振幅、位相、群遅延特性です。

Plot of ITU-R BS.1770-4 FIR filter responses.

群遅延特性の通過域が波打っているので SOCP FIR のように見えます。また群遅延特性から [5, 6) サンプルの遅れが加わることがわかりました。

計算方法はずっと下のほうにある「C++ での実装」に掲載しています。フィルタ係数を入れ替えて、 bufferSize = 12 、 intDelay = 5 と変更すれば計算できます。

BS.1770 FIR のフィルタ係数は末尾がどれも ...125, 375, 625, 875 などになっているので有理数で表現できそうです。以下は Maxima の rat を用いて有理数に変換したフィルタ係数です。

Phase0: [
  7/4096, 45/4096, -161/8192, 17/512,
  -487/8192, 1125/8192, 1991/2048, -419/4096,
  195/4096, -109/4096, 61/4096, -17/2048
];
Phase1: [
  -239/8192, 15/512, -53/1024, 365/4096,
  -341/2048, 1905/4096, 1597/2048, -1641/8192,
  13/128, -477/8192, 271/8192, -155/8192
];
Phase2: [
  -155/8192, 271/8192, -477/8192, 13/128,
  -1641/8192, 1597/2048, 1905/4096, -341/2048,
  365/4096, -53/1024, 15/512, -239/8192
];
Phase3: [
  -17/2048, 61/4096, -109/4096, 195/4096,
  -419/4096, 1991/2048, 1125/8192, -487/8192,
  17/512, -161/8192, 45/4096, 7/4096
];

分数ディレイフィルタを使ったトゥルーピークの計算方法は大まかに以下のようになります。

float process(float input)
{
  float truepeak = 0.0f;
  for (auto &fd : fractionalDelays) {
    float candidate = std::fabs(fd.process(input));
    truepeak = std::max(truepeak, candidate);
  }
  return truepeak;
}

fractionalDelays は分数ディレイフィルタをまとめた配列で、長さはオーバーサンプリングの倍率から 1 を引いた値と同じです。例えば 4 倍のオーバーサンプリングなら [0.0, 0.25, 0.5, 0.75] の分数ディレイを計算します。分数ディレイが 0.0 のときは入力サンプルをそのまま使えばいいので、実装を工夫すれば分数ディレイフィルタの計算を 1 つ省略できます。

以下のリンク先で各分数ディレイフィルタの実装例を読めます。

どの分数ディレイフィルタを使ってオーバーサンプリングをどのくらいにすればいいのかを決めるために評価を行います。以下の手順で絞り込みを行っています。

  1. EBU TECH 3341 のテストを通る、最小の分数ディレイフィルタの長さを求める。
  2. 1 で得られた分数ディレイフィルタの中から最も速いものを選ぶ。
  3. 2 で最も速かった分数ディレイフィルタのパラメータ設定について詳細を調べる。

EBU TECH 3341 の Table 1 (pp.10-11) にトゥルーピークのテストがいくつか載っています。以下は EBU TECH 3341 のダウンロードリンクです。

以下の表は EBU TECH 3341 の Table 1 のトゥルーピークのテストの意訳です。

意訳始め。

番号 テスト信号 予期される応答 (許容誤差)
15 信号 1 、 周波数 fs / 4 Hz 、振幅 0.50 FFS 、位相 0.0° のサイン波 −6.0 (+0.2/−0.4) dBTP
16 信号 1 、 周波数 fs / 4 Hz 、振幅 0.50 FFS 、位相 45.0° のサイン波 −6.0 (+0.2/−0.4) dBTP
17 信号 1 、 周波数 fs / 6 Hz 、振幅 0.50 FFS 、位相 60.0° のサイン波 −6.0 (+0.2/−0.4) dBTP
18 信号 1 、 周波数 fs / 8 Hz 、振幅 0.50 FFS 、位相 67.5° のサイン波 −6.0 (+0.2/−0.4) dBTP
19 信号 1 、 周波数 fs / 4 Hz 、振幅 1.41 FFS 、位相 45.0° のサイン波 +3.0 (+0.2/−0.4) dBTP
20 信号 2 、 0 サンプルオフセット 0.0 (+0.2/−0.4) dBTP
21 信号 2 、 1 サンプルオフセット 0.0 (+0.2/−0.4) dBTP
22 信号 2 、 2 サンプルオフセット 0.0 (+0.2/−0.4) dBTP
23 信号 2 、 3 サンプルオフセット 0.0 (+0.2/−0.4) dBTP

信号 1 と信号 2 の定義です。

  1. 合成されたトーンの全長は重要でないが、トーンの両端に 10 ms のフェードイン、フェードアウトを入れること。
  2. 周波数 fs / 6 Hz 、振幅 1.41 FFS のサイン波に、周波数 fs / 4 Hz、振幅 1.00 FFS のサイン波を 1 周期含む。 1 周期のサイン波の両端で位相が連続であること。信号は 4 * fs で合成され、先頭に 0 サンプルのオフセットを加えられた上で、ローパスフィルタをかけて、 fs にダウンサンプリングされる。合成されたトーンの全長は重要でないが、両端に短いフェードイン、フェードアウトを入れること。

意訳終わり。

合成されたトーンの全長は重要でない (the duration of the synthesized tone does not matter) とありますが、 sinc 補間を計算するときは信号の長さでトゥルーピークの値が変わることがあります。

dBTP はデシベルで表したトゥルーピークのことです。 dB はデシベル、 TP はトゥルーピークのことです。

ここでの評価は EBU によって用意されたテスト信号を使っています。テスト信号は以下のリンクからダウンロードできます。

それぞれの分数ディレイフィルタについて EBU TECH 3341 のテストを通る最小の次数を探しました。以下のリンクにテストコードを掲載しています。

結果は以下のようになりました。

分数ディレイ パラメータ
ラグランジュ補間 11 次
Thiran オールパス 12 次
SOCP FIR フィルタの長さ 12 、 omega_max=0.5 、 omega_density=1 、 delta_min=5

SOCP FIR のパラメータはフィルタの長さを BS.1770 FIR と同じ 12 に固定した上で、残りのパラメータの値を試行錯誤によって見つけました。

以降では EBU TECH 3341 に加えて freesound.org で集めたデータを使って誤差などを測定しています。データは freesound.org のトップページから Sounds -> Give me a random sound! と辿ってランダムにダウンロードしました。以下のリンク先に使用データの一覧を掲載しています。

上で調べた EBU TECH 3341 のテストを通るパラメータを使ったときに、どの分数ディレイフィルタが最も速く計算できるのかを調べました。

以下のリンクにベンチマークのコードを掲載しています。

コンパイラオプションは CMake に任せました。 Visual Studio 2019 をインストールした Windows 10 で cmake --build . --config release としてビルドしています。

今回の実装では、以下の順に計算が速いという結果が出ました。

  1. SOCP FIR と BS.1770 FIR
  2. Thiran オールパス
  3. ラグランジュ補間

SOCP FIR と BS.1770 FIR はフィルタの長さが同じなので計算時間も同じでした。これら 2 つの FIR と比べると Thiran オールパスは 2 倍、ラグランジュ補間は 4~5 倍ほどの計算時間がかかりました。

高速な SOCP FIR に注目してパラメータを設定します。

オーバーサンプリングの倍率とフィルタの長さを変えたときに SOCP FIR の誤差がどう変わるかを調べました。ここでは omega_max = 0.5 で固定しています。

ここでは sinc 補間によって計算されたトゥルーピークを真値、 SOCP FIR によって計算されたトゥルーピークの値を近似値としています。真値と近似値の間で以下の誤差を測りました。

近似値が真値よりも小さいことをアンダーリード、近似値が真値よりも大きいことをオーバーリードと呼んでいます。トゥルーピークの目的は離散信号を連続信号にしたときの歪みを抑えることです。アンダーリードのときの近似値に基づいて音量を下げても歪みが防げないので、別に分けて平均誤差を取りました。オーバーリードはついでに測りました。アンダーリードは全て負の値、オーバーリードは全て正の値の誤差なので、絶対値を使わずに平均を取っています。

一つの音のデータの誤差は以下の手順で計算しています。

  1. Sinc 補間によるトゥルーピークの真値の最大値を計算。
  2. SOCP FIR によるトゥルーピークの近似値の最大値を計算。
  3. 真値と近似値の差から、平均絶対誤差、アンダーリード、オーバーリードを計算。

SOCP FIR の他のパラメータは delta_min = N / 2 - 1 、 omega_density = 1 としています。 N はフィルタの長さです。

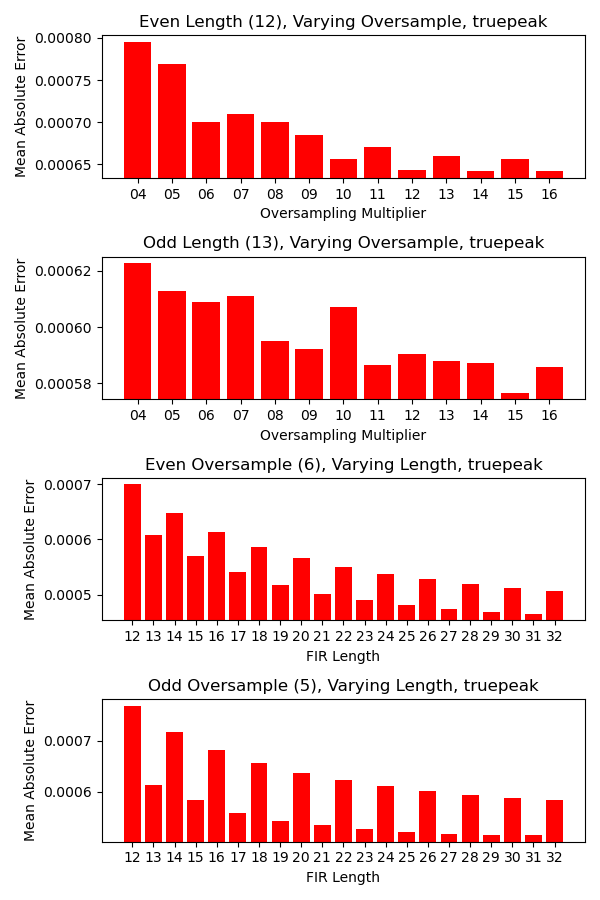
以下はオーバーサンプリングの倍率と SOCP FIR のフィルタの長さを変えたときのトゥルーピークの近似値の平均絶対誤差です。 1 つめのプロットを見るとフィルタの長さが偶数のときはオーバーサンプリングの倍率を偶数にしたほうが誤差が減るように見えます。 3 つめと 4 つめのプロットを見るとオーバーサンプリングの倍率が偶数、奇数のどちらであるかに関わらず、フィルタの長さが奇数のときに誤差が減っています。

Plot of absolute mean error of truepeak between sinc interpolation and SOCP FIR approximation.

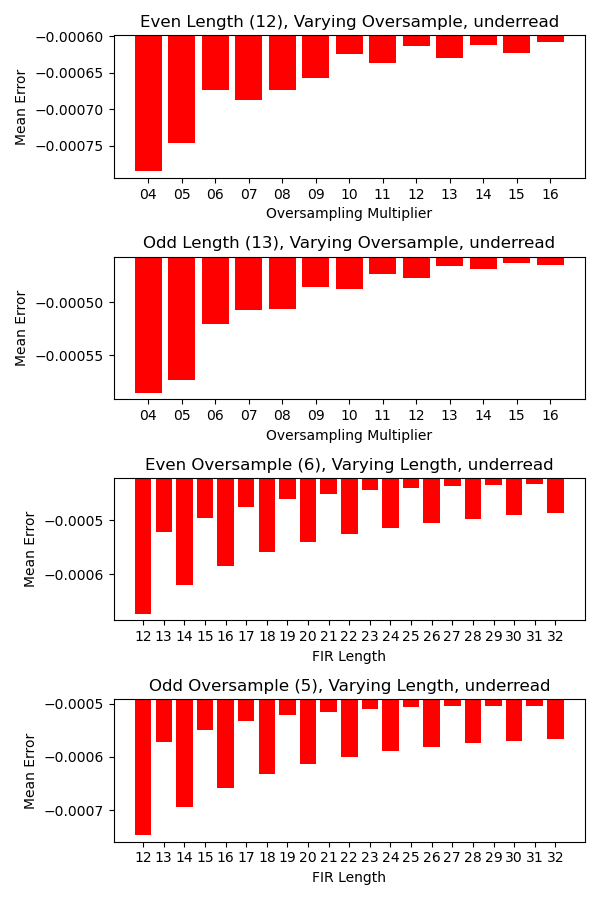
以下はオーバーサンプリングの倍率と SOCP FIR のフィルタの長さを変えたときのアンダーリードの平均誤差です。

平均絶対誤差のプロットと似たような傾向が見られます。縦軸の値に注目すると全体の誤差のうち、アンダーリードが占める割合がオーバーリードよりも大きいことがわかります。この傾向はデータセットによって変わるかもしれません。

2 つめのプロットを見るとフィルタの長さが奇数のときはオーバーサンプリングの倍率が奇数のときにアンダーリードが減っているように見えます。

Plot of mean error of underread.

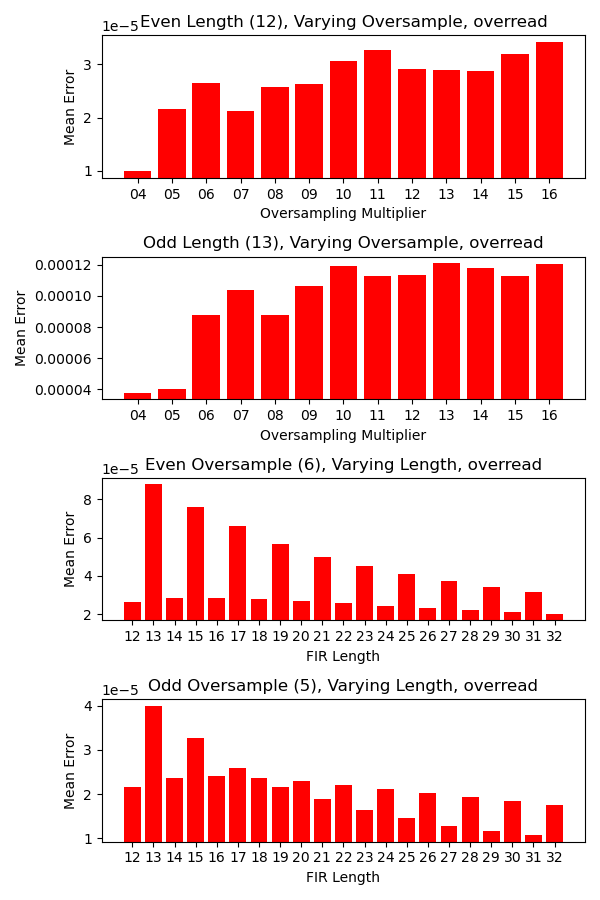
以下はオーバーサンプリングの倍率と SOCP FIR のフィルタの長さを変えたときのオーバーリードの平均誤差です。

1 つめと 2 つめのプロットを見るとオーバーサンプリングの倍率が低いほどオーバーリードが減る傾向があるように見えます。 3 つめと 4 つめのプロットを見るとオーバーリードはフィルタの長さが偶数のときに減るようです。

Plot of mean error of overread.

結果より SOCP FIR のパラメータは以下のように決めるとよさそうです。

オーバーサンプリングの倍率については一概には言えませんが、高いほどアンダーリードが減り、低いほどオーバーリードが減っているように見えます。フィルタの長さが偶数のときは、オーバーサンプリングの倍率が偶数になるとアンダーリードが減る傾向があるように見えます。同様にフィルタの長さが奇数のときはオーバーサンプリングの倍率が奇数のときにアンダーリードが減っているように見えます。

原則としてはアンダーリードを減らしつつ、全体の誤差も少なくしたいです。この要件を満たすにはフィルタの長さを奇数にして、オーバーサンプリングの倍率をできる限り高くすると良さそうです。

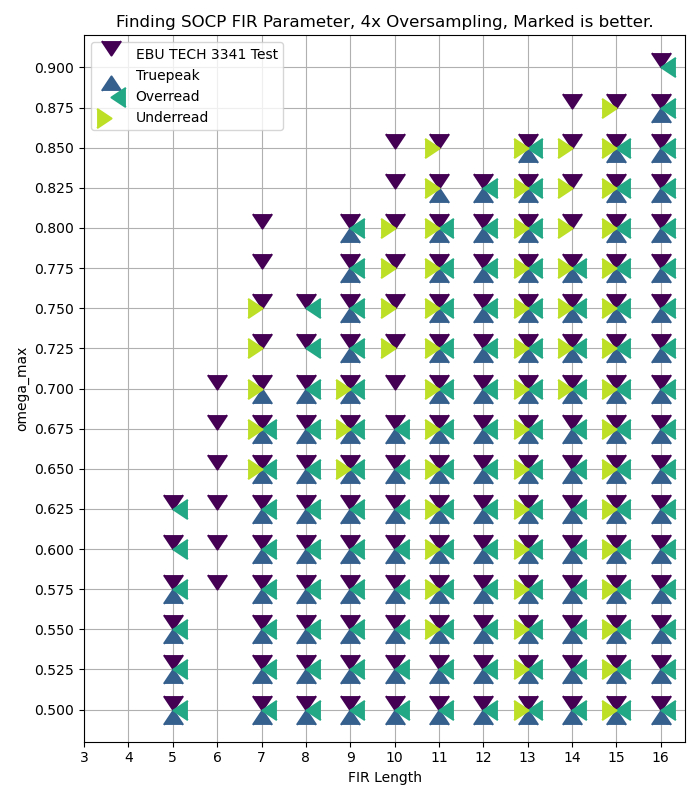
以下の図は SOCP FIR のパラメータを変えて EBU TECH 3341 のテストを通るかどうか、また BS.1770 FIR よりも誤差が小さいかどうかを調べた結果のプロットです。ここではオーバーサンプリングの倍率を 4 倍に固定してフィルタの長さと omega_max を変えています。マーカーがある箇所は EBU TECH 3341 テストを通った、あるいは BS.1770 FIR よりも誤差が小さかったことを示しています。つまり 4 つのマーカーが全て表示されているパラメータは質がいいと考えられます。

Plot of distribution of better SOCP FIR parameter.

以下の図は 4 つのマーカーが全て表示されているパラメータだけを抜き出したプロットです。

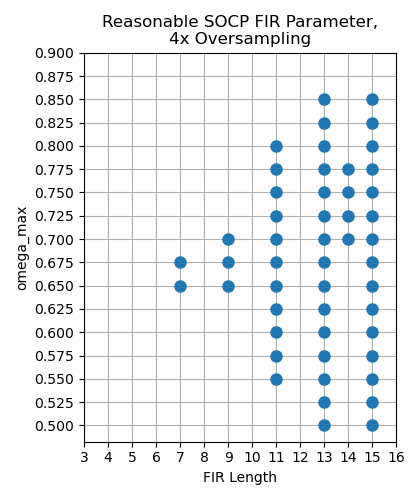
Summarized plot of distribution of better SOCP FIR parameter.

EBU TECH 3341 のテストを通り、 BS.1770 FIR よりも誤差の小さい SOCP FIR は以下のパラメータで設計できることがわかりました。

EBU TECH 3341 のテストを通るだけでいいならフィルタの長さは最小で 5 まで減らせそうです。

以下は誤差の比較です。フィルタの長さ 5 の SOCP FIR の誤差は測定した中で一番小さかったものを載せています。

{
  "ITU-R BS.1770 FIR": {
    "truepeak": 0.0011130596765247989,
    "overread": 0.0005132591093803915,
    "underread": -0.0005998005671444072
  },
  "SOCP FIR, Length=5, Oversample=4, omega_max=0.525": {
    "truepeak": 0.0010093198109477944,
    "overread": 0.00011114454719077043,
    "underread": -0.0008981752637570242
  },
  "SOCP FIR, Length=7, Oversample=4, omega_max=0.650": {
    "truepeak": 0.000835934970347886,
    "overread": 0.0002524608391844861,
    "underread": -0.0005834741311634001
  },
  "SOCP FIR, Length=7, Oversample=4, omega_max=0.675": {
    "truepeak": 0.0009051819175772438,
    "overread": 0.0003487720212173245,
    "underread": -0.0005564098963599192
  }
}

以下はフィルタの長さを 7 、 オーバーサンプリングの倍率を 4 倍とした SOCP FIR フィルタの特性です。

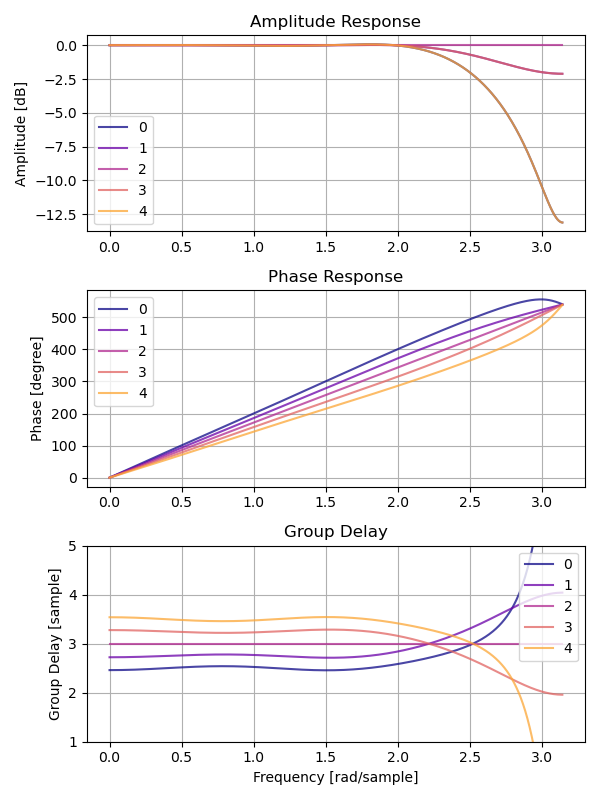
Plot of SOCP FIR filter responses. Length is 7, oversampling is 4x, and omega_max is 0.650.

SOCP FIR フィルタの長さを \(N\) とすると、遅延を \([N/2 - 1, N/2]\) の範囲で設定していること注意してください。このように遅延を設定すると誤差は減りますが、フィルタの長さが奇数のときに、群遅延特性がサンプル間ではなく、サンプルの前後に広がる形になります。例えばフィルタの長さが 15 なら [6.5, 7.5] の範囲で遅延を設定したほうが、 (6.0, 7.0) や (7.0, 8.0) と範囲を設定するよりも誤差が減ります。ただし、今回のデータセットでは遅延を \(\lfloor N/2 \rfloor - 1\) と設定したときでもフィルタの長さを奇数にしたほうが誤差が減りました。

インデックス 2 のフィルタは分数ディレイが 0.0 サンプルなので、入力サンプルをそのまま使うことで計算を省略できます。

インデックス 4 のフィルタも群遅延が平坦な部分については次の入力サンプルのインデックス 0 のフィルタと計算結果が重複するので、多少誤差が増えてもいいなら省略できます。以下はインデックス 4 のフィルタの有無による誤差の比較です。

{
  "SOCP FIR, Length=7, Oversample=4, omega_max=0.650": {
    "truepeak": 0.000835934970347886,
    "overread": 0.0002524608391844861,
    "underread": -0.0005834741311634001
  },
  "SOCP FIR, Length=7, Oversample=4, omega_max=0.650, without last index": {
    "truepeak": 0.0008398454979237256,
    "overread": 0.00023053871198559192,
    "underread": -0.0006093067859381339
  }
}

このフィルタについてはインデックス 4 を省略するとアンダーリードが BS.1770 FIR よりも大きくなるので、省略しないほうが良さそうです。

以下はインデックス 2 を省略したフィルタ係数です。インデックスは上から 0, 1, 3, 4 です。

[
  [
    0.03396642725330925, -0.12673821137646601, 0.5759982312324312, 0.6592123095604063,
    -0.19435321143573606, 0.0782612693103079, -0.025807862651826587
  ],
  [
    0.021616078095824397, -0.07539816970638001, 0.2653441329619578, 0.9081714824861011,
    -0.16017585860369898, 0.059489586593950955, -0.018863293456169244
  ],
  [
    -0.018863293456169286, 0.05948958659395098, -0.16017585860369907, 0.908171482486101,
    0.2653441329619578, -0.07539816970638011, 0.02161607809582444
  ],
  [
    -0.02580786265182662, 0.07826126931030812, -0.1943532114357363, 0.6592123095604064,
    0.5759982312324308, -0.12673821137646582, 0.033966427253309124
  ]
]

ここでは BS.1770 FIR より誤差が大きいものの、 EBU TECH 3341 のテストは通るフィルタを掲載しています。以下は SOCP FIR のパラメータです。

以下はフィルタ係数です。インデックスは上から 0, 1, 3, 4 です。インデックス 4 を省略するとテストを通らなくなります。

[
  [
    -0.0751360050029161, 0.5273409465119645, 0.678369080642087,
    -0.17854734458879204, 0.04698995690696311
  ],
  [
    -0.04390964025848337, 0.23798632863349117, 0.9146390367695467,
    -0.14391204608426109, 0.03486831203681682
  ],
  [
    0.03486831203681702, -0.1439120460842612, 0.9146390367695467,
    0.237986328633491, -0.04390964025848315
  ],
  [
    0.04698995690696286, -0.17854734458879132, 0.6783690806420861,
    0.5273409465119651, -0.07513600500291616
  ]
]

以下はフィルタの特性です。

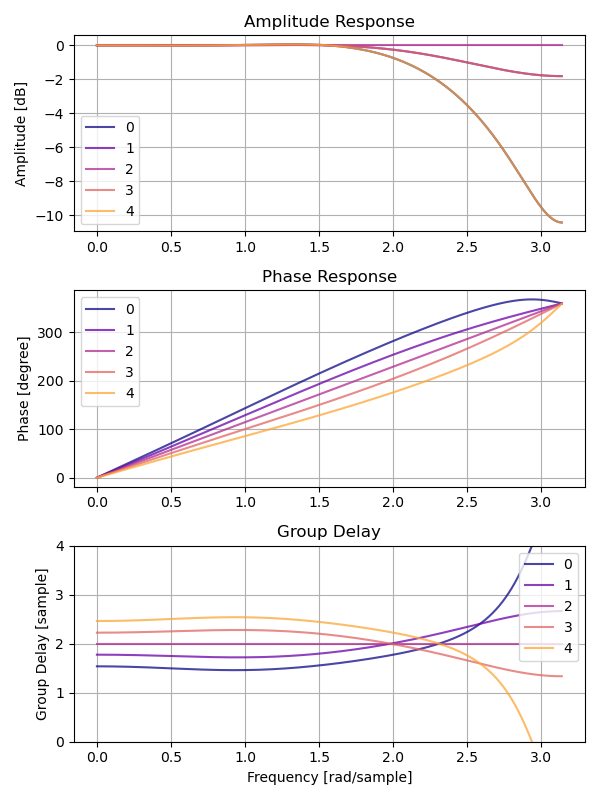
Plot of SOCP FIR filter responses. Length is 5, oversampling is 4x, and omega_max is 0.525.

フィルタの長さを 7 、 オーバーサンプリングを 4 倍、 omega_max を 0.65 とした SOCP FIR によるトゥルーピークメーターの C++17 での実装です。

#include <algorithm>
#include <array>
#include <iostream>

template<typename Sample> struct SOCPFIR {
  constexpr static size_t bufferSize = 7;
  constexpr static size_t intDelay = 3;

  constexpr static std::array<std::array<Sample, bufferSize>, 4> coefficient{{
    {Sample(0.03396642725330925), Sample(-0.12673821137646601),
     Sample(0.5759982312324312), Sample(0.6592123095604063), Sample(-0.19435321143573606),
     Sample(0.0782612693103079), Sample(-0.025807862651826587)},
    {Sample(0.021616078095824397), Sample(-0.07539816970638001),
     Sample(0.2653441329619578), Sample(0.9081714824861011), Sample(-0.16017585860369898),
     Sample(0.059489586593950955), Sample(-0.018863293456169244)},
    {Sample(-0.018863293456169286), Sample(0.05948958659395098),
     Sample(-0.16017585860369907), Sample(0.908171482486101), Sample(0.2653441329619578),
     Sample(-0.07539816970638011), Sample(0.02161607809582444)},
    {Sample(-0.02580786265182662), Sample(0.07826126931030812),
     Sample(-0.1943532114357363), Sample(0.6592123095604064), Sample(0.5759982312324308),
     Sample(-0.12673821137646582), Sample(0.033966427253309124)},
  }};
};

template<typename Sample, typename FractionalDelayFIR> class TruePeakMeterFIR {
  std::array<Sample, FractionalDelayFIR::bufferSize> buf{};

public:
  void reset() { buf.fill(Sample(0)); }

  Sample process(Sample input)
  {
    for (size_t i = 0; i < buf.size() - 1; ++i) buf[i] = buf[i + 1];
    buf.back() = input;

    Sample max = std::fabs(buf[FractionalDelayFIR::intDelay]);
    for (const auto &phase : FractionalDelayFIR::coefficient) {
      Sample sum = 0;
      for (size_t i = 0; i < phase.size(); ++i) sum += buf[i] * phase[i];
      max = std::max(max, std::fabs(sum));
    }
    return max;
  }
};

int main()
{
  // 1 サンプルだけ計算する例。
  TruePeakMeterFIR<float, SOCPFIR<float>> bs1770;
  std::cout << bs1770.process(1.0f) << "\n";

  return 0;
}

理論上のトゥルーピークの最大値がどれくらいになるのかを調べます。

ここでは離散信号の絶対値の最大値を離散ピークと呼びます。 \(x\) を入力信号とすると以下の式で離散ピーク \(P\) が計算できます。

\[ P(x) = \max(|x|) \]

Sinc 補間の式を再掲します。

\[ x(t) = \sum_{n=-\infty}^{\infty} x[n] \mathrm{sinc} \left( t - n \right) \]

ダイナミックレンジの範囲を \([-1, 1]\) とすると、離散信号 \(x[n]\) が \(\mathrm{sgn}(\mathrm{sinc}(t - n))\) のときに離散ピークと sinc 補間から得られるトゥルーピークの差が最大になります。 \(\mathrm{sgn}\) は 符号関数 です。以降では離散ピークとトゥルーピークの差が最大になる場合を、最悪の場合と呼びます。

以下は \(x[n]\) に \(\mathrm{sgn}(\mathrm{sinc}(t - n))\) を代入した、最悪の場合の sinc 補間の式です。

\[ \begin{aligned} \hat{x}(t) &= \sum_{n=-\infty}^{\infty} \mathrm{sgn}(\mathrm{sinc}(t - n)) \mathrm{sinc} \left( t - n \right)\\ &= \sum_{n=-\infty}^{\infty} |\mathrm{sinc} \left( t-n \right)|\\ &= \sum_{n=-\infty}^{\infty} \left| \frac{\sin(\pi (t-n))}{\pi(t-n)} \right|\\ \end{aligned} \]

よくわからないので適当に範囲などを変えた式を Wolfram Alpha に入力したところ以下のような出力が得られました。

sum_(x=0)^n abs(sin(π (x + 0.5))/(π (x + 0.5)))
  ≈ 0.31831 (polygamma(0, n + 1.5) + 1.96351)

polygamma(0, ...) は次数 0 の polygamma function です。 Polygamma function の次数が 0 のときは digamma function になるそうです。

\[ \mathtt{polygamma}(n, z) = \psi^{(n)}(z) = \frac{d^{(n+1)}}{d z^{(n+1)}} \ln \Gamma(z) \]

Digamma function は \(0\) から \(\infty\) までの総和の形に変形できるようなので最悪の場合の sinc 補間の式をさらに変形します。

\[ \begin{aligned} \hat{x}(t) &= \sum_{n=-\infty}^{\infty} \left| \frac{\sin(\pi (t-n))}{\pi(t-n)} \right|\\ &= \sum_{n=-\infty}^{0} \left| \frac{\sin(\pi (t-n))}{\pi(t-n)} \right| + \sum_{n=1}^{\infty} \left| \frac{\sin(\pi (t-n))}{\pi(t-n)} \right|\\ &= \sum_{n=0}^{\infty} \left| \frac{\sin(\pi (t+n))}{\pi(t+n)} \right| + \sum_{n=0}^{\infty} \left| \frac{\sin(\pi (t-n-1))}{\pi(t-n-1)} \right|\\ \end{aligned} \]

総和のインデックスを \(0\) から \(\infty\) に変形しました。さらに \(t \in [0, 1]\) と制限すれば絶対値の計算を外すことができます。 \(t \in [0, 1]\) と制限する操作は離散信号のインデックスを \(- \mathrm{floor}(t)\) ずらすことと同じです。

2 つの総和の分母は \(t \in [0, 1]\) の条件と、三角関数の \(\sin(\pi n + t) = \pm \sin(t)\) という性質から以下のように変形できます。

\[ \begin{aligned} |\sin(\pi (t+n)))| &= \sin(\pi t)\\ |\sin(\pi (t-n-1))| &= -\sin(\pi (t - 1))\\ \end{aligned} \]

2 つの総和の分子は \(t \in [0, 1]\) かつ \(n \geq 0\) という条件から以下のように変形できます。

\[ \begin{aligned} |\pi(t+n)| &= \pi(t+n)\\ |\pi(t-n-1)| &= \pi(n + 1 - t)\\ \end{aligned} \]

最悪の場合の sinc 補間の式をさらに変形します。

\[ \begin{aligned} \hat{x}(t) &= \sum_{n=0}^{\infty} \left| \frac{\sin(\pi (t+n))}{\pi(t+n)} \right| + \sum_{n=0}^{\infty} \left| \frac{\sin(\pi (t-n-1))}{\pi(t-n-1)} \right|\\ &= \frac{\sin(\pi t)}{\pi} \sum_{n=0}^{\infty} \frac{1}{t+n} - \frac{\sin(\pi (t - 1))}{\pi} \sum_{n=0}^{\infty} \frac{1}{n+1-t}\\ \end{aligned} \]

総和を片方ずつ Wolfram Alpha に入れたところ以下の部分総和の式が出てきました。

sum_(n=0)^m sin(π t)/(π (t + n))
  = (
      sin(π t) polygamma(0, t + m + 1)
    - sin(π t) polygamma(0, t)
    )/π

sum_(n=0)^m sin(π (t - 1))/(π (n + 1 - t))
  = (
      sin(π (t - 1)) polygamma(0, -t + m + 2)
    - sin(π (t - 1)) polygamma(0, 1 - t)
    )/π

前述のように次数 0 の polygamma function \(\psi^{(0)}(z)\) は digamma function \(\psi(z)\) です。また \(\psi(\infty)\) は無限なので \(m \to \infty\) の極限をとれば、最悪の場合の sinc 補間の式は発散します。

\[ \begin{aligned} \lim_{m \to \infty} \hat{x}(t) &= \lim_{m \to \infty} \left( \frac{\sin(\pi t)}{\pi} \sum_{n=0}^{m} \frac{1}{t+n} - \frac{\sin(\pi (t - 1))}{\pi} \sum_{n=0}^{m} \frac{1}{n+1-t} \right)\\ &= \lim_{m \to \infty} \left( \frac{\sin(\pi t)}{\pi} (\psi(t + m + 1) - \psi(t)) - \frac{\sin(\pi (t - 1))}{\pi} (\psi(-t + m + 2) - \psi(1 - t)) \right)\\ &= \frac{\sin(\pi t)}{\pi} (\infty - \psi(t)) - \frac{\sin(\pi (t - 1))}{\pi} (\infty - \psi(1 - t))\\ &= + \infty \end{aligned} \]

よって離散ピークとトゥルーピークの差は最悪の場合、無限になります。ただし、信号の長さが有限なら差も有限になりそうです。

信号の長さが有限のときの差の最大値について調べます。 Digamma function による計算のコードです。

# Python3
import numpy as np
from scipy.special import psi

def calcWorstTruePeak(nSample, fraction=0.5):
    m = nSample // 2
    t = fraction
    A = (psi(t + m + 1) - psi(t)) * np.sin(np.pi * t) / np.pi
    B = (psi(-t + m + 2) - psi(1 - t)) * np.sin(np.pi * (t - 1)) / np.pi
    return A - B

Digamma function を使う方法の他に、総和を for 文で愚直に計算するコードも書いて同じ値が出るのか確認しました。確認用に書いたコードは以下のリンク先に掲載しています。

結果です。これらは最悪の場合の値なので、実際の差はより小さくなるはずです。

信号の長さ サンプル数 差の最大値 (fs=48000) dB (fs=48000)
1 秒 1 * fs 15.06330969705911 23.55840810296123
1 分 60 * fs 20.27634709353383 26.13979433865427
1 時間 60 * 60 * fs 25.4894283622857 28.12720191778964
1 日 24 * 60 * 60 * fs 29.53585217059294 29.406990113422037

差の最大値とは、最悪の場合の信号の離散ピークとトゥルーピークの差の最大値です。 dB はダイナミックレンジを [-1.0, 1.0] として、差の最大値をデシベルに変換した値です。

理論上は離散ピークとトゥルーピークの差の最大値は無限に発散します。

計算上は信号の長さが有限なので、差の最大値も有限になります。差の最大値は以下の式で計算できます。

\[ \begin{aligned} P_{\mathrm{sinc}}(\hat{x}, t) - P(\hat{x}) &= \begin{cases} 1, & \text{if}\quad t \bmod 1 = 0,\\ D(t, N/2), & \text{otherwise}. \end{cases}\\\\ D(t, m) &= \left( \frac{\sin(\pi t)}{\pi} (\psi(t + m + 1) - \psi(t)) - \frac{\sin(\pi (t - 1))}{\pi} (\psi(-t + m + 2) - \psi(1 - t)) \right) - 1 \end{aligned} \]

パラメータ一覧。

関数一覧。

\(t = 0.5\) のときは差の計算式を以下に簡略化できます。

\[ D(0.5, m) = \frac{2}{\pi} (\psi(m + 1.5) - \psi(0.5)) - 1 \]

32 bit や 64 bit の浮動小数点数で計算するときは小さい値が丸めによって無視されるので sinc 補間のフィルタのタップ数を有限の長さで打ち切ることができそうです。以下のようなコードを書いて調べてみました。

// C++
#include <cmath>
#include <iostream>

template<typename T> T sinc(T x) { return x != 0 ? std::sin(x) / x : T(1); }
template<typename T> T toDecibel(T x) { return T(20) * std::log10(x); }

template<typename FLOAT> void testSincWidth(uint64_t step = 1, uint64_t start = 0)
{
  uint64_t i = start;
  int exponent = 0;
  while (exponent > -std::numeric_limits<FLOAT>::digits) {
    FLOAT value = sinc(FLOAT(i));
    std::frexp(value, &exponent);
    i += step;
  }
  std::cout << i << ": " << sinc(FLOAT(i)) << ", " << exponent << "\n";
}

int main()
{
  testSincWidth<float>();
  testSincWidth<double>(10000);
}

Sinc 関数の最大値は 1 です。よって浮動小数点数で表された 1.0 と sinc(x) の指数部の差が std::numeric_limits<FLOAT>::digits 以上なら丸め誤差によって無視されます。上のコードの while の条件式でこの判断をしています。 1.0 の指数部は 1 ですが、上のコードでは省略して while(exponent > -digits) としています (1 - exponent <= digits と等価) 。

出力されたインデックスは float で 61394 、 double で 2223497001 となりました。上のコードでは sinc 関数の片側だけを見ているので、得られたインデックスを m とすると、少なくとも 2 * m - 1 の長さのタップ数が必要になります。このアプローチの実用性はなさそうです。

出力されたインデックス以降で浮動小数点数の丸めによって切り捨てられない大きさの値が現れないことは確認していないので注意してください。