何かあれば GitHub のリポジトリに issue を作るか ryukau@gmail.com までお気軽にどうぞ。
Update: 2025-01-07
Putnam と Smith による Design of Fractional Delay Filters Using Convex Optimization に沿って分数ディレイフィルタを設計します。
論文の問題をまとめると、次の second-order cone problem の形になります。
\[ \begin{aligned} \text{minimize} \quad & t\\ \text{subject to} \quad & \lVert \mathbf{\tilde{A}}_i \mathbf{x} - \mathbf{b}_i \rVert_2 < \mathbf{t} ,\quad i \in 1, \dots, M\\ \text{where}\quad & \mathbf{\tilde{A}}_i = \begin{bmatrix} \mathrm{Re}(\mathbf{a}_i^T) & 0\\ \mathrm{Im}(\mathbf{a}_i^T) & 0 \end{bmatrix} ,\quad \mathbf{b}_i = \begin{bmatrix} \mathrm{Re}(H_d(\omega_i))\\ \mathrm{Im}(H_d(\omega_i)) \end{bmatrix} ,\quad \mathbf{t} = \begin{bmatrix} t\\ t \end{bmatrix} ,\\ & \mathbf{x}^T = \begin{bmatrix} \mathbf{h}^T & t \end{bmatrix} ,\\ & \mathbf{a}_i^T = \begin{bmatrix} 1 & e^{-j \omega_i} & e^{-2 j \omega_i} & \dots & e^{-(N-1) j \omega_i} \end{bmatrix} ,\\ & H_d(\omega_i) = e^{-j \Delta \omega_i} ,\\ & \omega_i = \omega_{\max} \frac{i}{M}. \end{aligned} \]
パラメータの一覧です。
ここで求めたい値は \(\mathbf{h}\) です。
\(t\) はスラック変数 (slack variable) です。ソルバで解いた値は \(\mathbf{x}\) の形で出力されますが、最後の要素 \(t\) は不要なので捨てることになります。
任意の分数サンプルのディレイを行いたいので \(\Delta\) を一つの値ではなく範囲で指定します。実装では任意の \(\Delta_{\min}\) から \(\Delta_{\min} + 1\) の範囲でフィルタ係数を計算しています。
Python3 で CVXOPT の solvers.socp
を使って問題を解きます。
import json
import numpy
from cvxopt import matrix, solvers
def get_b(omega, delta):
H_d = numpy.exp(-1j * delta * omega)
return numpy.vstack((H_d.real, H_d.imag)).T
def get_A_tilde(n_taps, omega):
index = numpy.arange(n_taps)
a = numpy.exp(-1j * index.reshape(1, -1) * omega.reshape(-1, 1))
A_tilde = []
for a_i in a:
a_i0 = numpy.append(a_i, 0)
A_tilde.append([a_i0.real, a_i0.imag])
return numpy.array(A_tilde)
def solve(A, b):
c = numpy.zeros(A.shape[2])
c[-1] = 1
rhs = numpy.zeros_like(A[0][0])
rhs[-1] = 1
G = [matrix(-numpy.vstack((rhs.reshape(1, -1), A_i))) for A_i in A]
h = [matrix(numpy.append(0, b_i)) for b_i in b]
sol = solvers.socp(matrix(c), Gq=G, hq=h)
return numpy.array(sol["x"]).flatten()
def createTable(n_taps, n_fraction, delta_min=None, omega_max=0.9,, omega_density=4):
omega = numpy.linspace(
0,
numpy.pi * omega_max,
omega_density * n_taps,
)
if delta_min is None:
delta_min = numpy.floor(n_taps / 2)
table = [
-solve(get_A_tilde(n_taps, omega), get_b(omega, delta))[0:-1]
for delta in numpy.linspace(delta_min, delta_min + 1, n_fraction)
]
return {
"delta_min": delta_min,
"omega_max": omega_max,
"table": numpy.array(table),
}
if __name__ == "__main__":
table = createTable(32, 11)
table["table"] = table["table"].tolist()
with open("table.json", "w") as outfile:
json.dump(table, outfile)計算結果は table.json に出力されます。
任意の \(\Delta\) を指定するときはテーブルを線形補間します。
import json
import numpy
import scipy.signal as signal
def get_filter_coefficients(table_data, delta):
if delta < 0 or delta > 1:
return None
elif delta == 1:
return numpy.array(table_data["table"])[-1]
table = numpy.array(table_data["table"])
length = table.shape[0] - 1
pos = delta * length
low = int(pos)
return table[low] + (pos - low) * (table[low + 1] - table[low])
with open("table.json", "r") as infile:
table_data = json.load(infile)
fir = get_filter_coefficients(table_data, 0.45)
source = signal.unit_impulse(32)
dest = signal.lfilter(fir, [1], source)設計したフィルタの群遅延です。横軸に平行な直線になるのが理想ですが波打っています。

似たような次数のラグランジュ補間の群遅延特性です。ラグランジュ補間のフィルタの長さは次数 + 1になります。
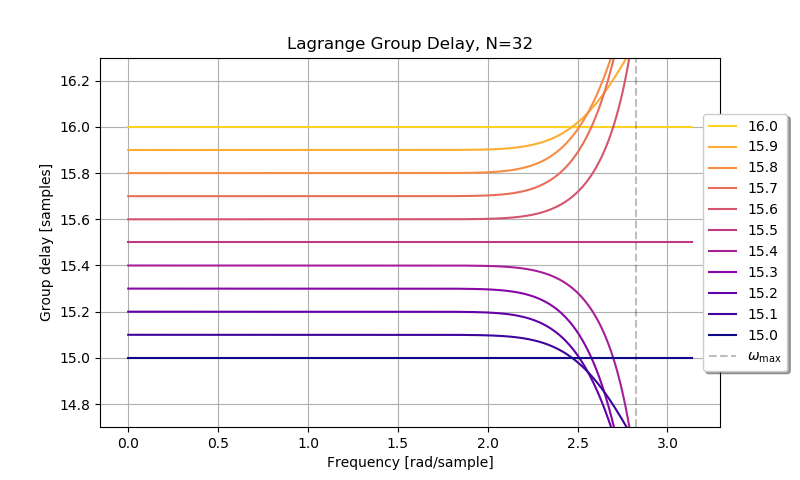
低域での特性はラグランジュ補間のほうが良さそうです。 \(\omega_{\max}\) に近くなるほどSOCPを解いて設計したフィルタのほうが誤差が少ないように見えます。
\(N\) は奇数よりも偶数のほうが誤差が小さくなります。また \(N\) が大きくなるほど誤差が減ります。
ディレイ時間は \(\Delta \in [\mathrm{floor}((N-1)/2),\,\mathrm{floor}((N+1)/2)]\) で固定します。整数ディレイを0にできないかと思い \(\Delta \in [0,\,1]\) と設定してみたのですが、フィルタ係数がやたら大きくなって通過した信号が0dBを超えました。
\(\omega_{\max} = 0.5 \pi\) にすると通過域での誤差が大きく減ります。オーバーサンプリングと組み合わせると \(\omega_{\max} = 0.9 \pi\) としたときよりもディレイ時間を変えたときのノイズが減りました。
\(M = 4N\) で固定します。 \(\omega_{\max} = 0.5 \pi\) のときは \(M = 4N\) で誤差が少なくなります。 \(\omega_{\max} = 0.9 \pi\) のときは \(M = N\) としたほうが誤差が減りました。
\(\Delta\) と \(M\) はパラメータの設定で決めた値に固定します。8倍、16倍、32倍という表記はオーバーサンプリングの倍率を表しています。凸最適化を用いて設計した分数ディレイフィルタのことをSOCP-FDフィルタと略しています。
サイン波をディレイ時間を変えて変調したサンプルです。
Math.random()
で生成したノイズをディレイ時間を変えて低速再生したサンプルです。
ラグランジュ補間でいいような気がします。
SOCP-FDフィルタを使うときは \(\omega_{\max}=0.5\) としてオーバーサンプリングしたほうが良さそうです。
\(\lVert \chi \rVert_2\) は \(\ell^2\) ノルムです。
論文では \(c_i^T x\) と \(f^T x\) が出てきますが、式変形を追いかけると \(c_i^T x = f^T x = t\) なのでこの文章では単に \(t\) としています。
論文中に出てくる \(\Re, \Im\) は
\(\TeX\) の \Re, \Im
です。この文章では \(\mathrm{Re},
\mathrm{Im}\) の表記に変えています。
CVXOPT の matrix は Python の list
を渡したときと、 NumPy の ndarray
を渡したときで行と列の順序が逆になります。
>>> import numpy
>>> from cvxopt import matrix, solvers
>>>
>>> a = numpy.arange(6).reshape(2, 3)
>>> a
array([[0, 1, 2],
[3, 4, 5]])
>>> a.tolist()
[[0, 1, 2], [3, 4, 5]]
>>> print(matrix(a)) # ndarray
[ 0 1 2]
[ 3 4 5]
>>> print(matrix(a.tolist())) # list
[ 0 3]
[ 1 4]
[ 2 5]
>>> numpy.array(matrix(a.tolist())) # a が転置してしまう。
array([[0, 3],
[1, 4],
[2, 5]])
>>> print(matrix(numpy.arange(4))) # 1次元の ndarray は列ベクトルになる。
[ 0]
[ 1]
[ 2]
[ 3]
>>> print(matrix([0, 1, 2, 3])) # 1次元の list も列ベクトルになる。
[ 0]
[ 1]
[ 2]
[ 3]CVXOPT のユーザガイドの例では list が使われているので
ndarray を使うときは転置に注意する必要があります。
\mathrm{subject to} を \text{subject to}
に修正。
\mathrm を使うと Firefox 82.0 で subject と to
の間のスペースが表示されない。