何かあれば GitHub のリポジトリに issue を作るか ryukau@gmail.com までお気軽にどうぞ。
Update: 2025-01-07
クラスタリングの特徴量として使うために単音からのピッチ推定を実装します。ここでのピッチとは音の基本周波数を指しています。
Python3のライブラリを探したところ、Essentiaに含まれていたYINというピッチ推定のアルゴリズムを見つけました。そこからさらに調べると sevagh さんのリポジトリ を見つけて McLeod pitch method (MPM) を見つけました。
ここでは YIN と MPM を実装して評価します。 MPM という呼び方は sevagh さんにならっています。
YINの処理の流れは次のようになります。
Cumulative mean normalized difference は次のように定義されています。式中の \(x[i]\) は配列 \(x\) のインデックス \(i\) の値を意味します。 \(t\) は入力信号の区間のインデックスです。
\[ d'_t[\tau] = \begin{cases} 1, &\text{if }\tau = 0,\\ \dfrac{d_t[\tau]}{(1/\tau) \sum_{j=0}^{\tau-1}d_t[j]}, &\text{otherwise.} \end{cases} \]
\(d\) はYINの論文で difference function と呼ばれている関数で、次のように定義されています。式中の \(N\) は入力信号のサンプル数です。論文では \(N\) ではなく \(W\) を使っています。
\[ \begin{aligned} d_t[\tau] &=\sum_{j=t}^{t + N - 1} (x[j] - x[j+\tau])^2\\ &=r_t[0] + r_{t + \tau}[0] - 2r_t[\tau] \end{aligned} \]
\(r\) は自己相関関数 (autocorrelation function) で、YINの論文では2つの定義が紹介されています。Type I, type II という名前はMPMの論文に従っています。
\[ \begin{aligned} r_t[\tau] &= \sum_{j=t}^{t + N - 1} x[j] x[j + \tau],\qquad\text{Type I}\\ r'_t[\tau] &= \sum_{j=t}^{t + N - \tau - 1} x[j] x[j + \tau],\quad\text{Type II} \end{aligned} \]
これらの式を見たとき \(t\) と \(\tau\) について混乱したのでまとめます。
\(t\)
は今からピッチを推定したい信号の、自己相関を計算する区間の開始時点を表しています。
FFT を用いるときによくあるのですが、信号を \(2^n\)
サンプルごとなどに分割して処理することを想定しているようです。後で出てくる
python_speech_features.sigproc.framesig
はこの分割を行う関数です。信号全体から一つのピッチの値を取り出したいときは、信号の開始時点を
\(t=0\)
と考えることができます。以降では 1
区間での計算だけを扱うので簡略化のために常に \(t=0\) とします。
\(\tau\) は自己相関を計算する区間のインデックスを表しています。信号全体の自己相関を計算するとき \(\tau\) の範囲は \([0, N -1]\) になります。
またYINの論文の fig. 1. (c) を見ると type I の自己相関の計算では \(x\) が周期 \(N\) で反復することを仮定しているようです。 type II の自己相関の計算では \(x\) のインデックスが \([0, N - 1]\) の範囲外のとき \(x\) の値を0としています。
自己相関は相互相関の特殊な場合です。相互相関関数 \(C\) は次のように定義できます。
\[ C_(x,y)[\tau] = \sum_{j=0}^{N - \tau - 1} x[j] y[j + \tau] \]
相互相関関数はFFTを使って高速に計算することができます。 \(^{*}\) は複素共役を表しています。
\[ C(x, y) \iff \mathtt{ifft}(\mathtt{fft}(x)(\mathtt{fft}(y))^{*}) \]
自己相関関数 \(r'_t\) は \(C\) を使って次のように書けます。
\[ r' = C(x, x) \iff \mathtt{ifft}(\mathtt{fft}(x)(\mathtt{fft}(x))^{*}) \]
FFTでは入力信号が無限に反復する信号の1周期ということを仮定しています。つまり \(x\) をそのまま使うと type I の自己相関の計算になります。 Type II の自己相関を計算するときは \(x\) の後に、 \(x\) 以上に長い0ベクトルをつなげてから計算すればいいようです。
\[ x' = (x[0], x[1],...,x[N-1],0,0,...,0), \quad\mathtt{len}(x') \geq 2N \]
実装します。
import numpy
from pyfftw.interfaces.numpy_fft import fft, ifft
def autocorrelation_type1(sig):
len_sig = len(sig)
spec = fft(sig)
return ifft(spec * spec.conj()).real[:len_sig]
def autocorrelation_type2(sig):
len_sig = len(sig)
sig = numpy.pad(sig, (0, len_sig), "constant")
spec = fft(sig)
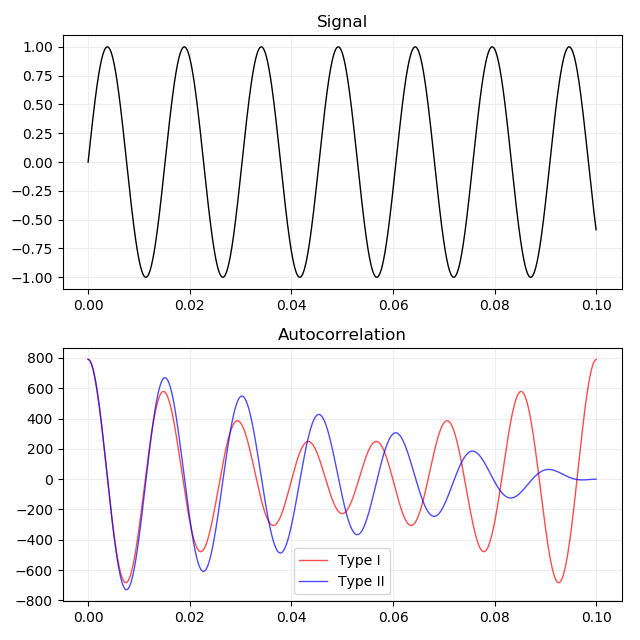
return ifft(spec * spec.conj()).real[:len_sig]66Hz、0.1秒のサイン波の自己相関のプロットです。横軸は時間で縦軸は信号の大きさです。

YINの論文では type I の自己相関関数を使った difference function だけを扱っています。ここでは type II も試します。
Difference function を再掲します。
\[ d_t[\tau]=r_t[0] + r_{t + \tau}[0] - 2r_t[\tau] \]
\(t=0\) として type I の自己相関について \(r_{t + \tau}[0]\) と \(r_t[0]\) を展開します。
\[ \begin{aligned} r_{\tau}[0] &= \sum_{j=\tau}^{\tau + N - 1} x^2[j]\\ r[0] &= \sum_{j=0}^{N - 1} x^2[j] \end{aligned} \]
Type I の自己相関では \(x\) の周期が \(N\) なので \(r_{\tau}[0] = r[0]\) となります。例として \(N = 3, \tau = 2\) のときを考えます。
\[ \begin{aligned} r_{2}[0] &= \sum_{j=2}^{2 + 3 - 1} x^2[j]\\ &= x^2[2] + x^2[3] + x^2[4]\\ &= x^2[2] + x^2[0] + x^2[1]\\ &= \sum_{j=0}^{3 - 1} x^2[j]\\ &= r[0]\\ \end{aligned} \]
よって type I の自己相関を使う difference function を次のように変形できます。
\[ \begin{aligned} d[\tau] &= r[0] + r_{\tau}[0] - 2r[\tau]\\ &= 2 (r[0] - r[\tau]) \end{aligned} \]
\(d\) を \(\tau > 0\) のときの cumulative mean normalized difference function に展開します。
\[ \begin{aligned} d'[\tau] &= \dfrac{d[\tau]}{(1/\tau) \sum_{j=0}^{\tau-1}d[j]}\\ &= \dfrac{2 (r[0] - r[\tau])}{(1/\tau) \sum_{j=0}^{\tau-1}2 (r[0] - r[j])}\\ &= \dfrac{(r[0] - r[\tau])}{(1/\tau) \sum_{j=0}^{\tau-1}(r[0] - r[j])} \end{aligned} \]
係数の2を消すことができました。最終的に type I の自己相関を使う difference function は次のように簡略化できます。
\[ d[\tau] = r[0] - r[\tau] \]
\(t=0\) として type II の自己相関について \(r_{t + \tau}[0]\) と \(r_t[0]\) を展開します。
\[ \begin{aligned} r'_{\tau}[0] &= \sum_{j=\tau}^{N - 1} x^2[j]\\ r'[0] &= \sum_{j=0}^{N - 1} x^2[j] \end{aligned} \]
Type II の自己相関を使うときは特に変形できなさそうです。
実装します。
def difference_type1(sig):
autocorr = autocorrelation_type1(sig)
return autocorr[0] - autocorr
def difference_type2(sig):
autocorr = autocorrelation_type2(sig)
energy = (sig * sig)[::-1].cumsum()[::-1]
return energy[0] + energy - 2 * autocorr
def cumulative_mean_normalized_difference(diff):
diff[0] = 1
sum_value = 0
for tau in range(1, len(diff)):
sum_value += diff[tau]
diff[tau] /= sum_value / tau
return diff
sig = get_some_signal() # 任意の入力信号を取得。
diff = difference_type1(sig)
cmnd = cumulative_mean_normalized_difference(diff)66Hz、0.1秒のサイン波の自己相関のプロットです。横軸は時間で縦軸は信号の大きさです。
論文ではしきい値以下の局所最小点のインデックスを探すステップを absolute threshold と呼んでいます。探索は cumulative mean normalized difference のインデックス0から行います。探索で見つけたインデックスは信号の1周期にかかる時間の推定値です。
Absolute threshold のステップで得られたインデックスを使って parabolic interpolation で離散化される前の信号の局所最小点のインデックスを推定します。
Parabolic interpolation は次の式で計算できます。 \(i_1\) が absolute threshold のステップで得られたインデックスです。
\[ i_{min} = i_1 + \frac{1}{2} \frac{ (x[i_0] - x[i_1])(i_2 - i_1)^2 - (x[i_2] - x[i_1])(i_1 - i_0)^2 }{ (x[i_0] - x[i_1])(i_2 - i_1) + (x[i_2] - x[i_1])(i_1 - i_0) } \]
\(i_0, i_1\) は配列の隣り合うインデックスなので \(i_1 - i_0 = 1\) となります。 \(i_2, i_1\) についても同様に \(i_2 - i_1 = 1\) です。 Parabolic interpolation の式に代入します。
\[ \begin{aligned} i_{min} &= i_1 + \frac{1}{2} \frac{ (x[i_0] - x[i_1]) - (x[i_2] - x[i_1]) }{ (x[i_0] - x[i_1]) + (x[i_2] - x[i_1]) }\\ &= i_1 + \frac{1}{2} \frac{x[i_0] - x[i_2]}{x[i_0] + x[i_2] - 2x[i_1]} \end{aligned} \]
得られたインデックスでサンプリング周波数を割ると周波数が推定できます。
YIN_THRESHOLD = 0.3 # 任意の正の値のしきい値。
def absolute_threshold(diff, threshold=YIN_THRESHOLD):
tau = 2
while tau < len(diff):
if diff[tau] < threshold:
while tau + 1 < len(diff) and diff[tau + 1] < diff[tau]:
tau += 1
break
tau += 1
return None if tau == len(diff) or diff[tau] >= threshold else tau
def parabolic_interpolation(array, x):
x_result = None
if x < 1:
x_result = x if array[x] <= array[x + 1] else x + 1
elif x >= len(array) - 1:
x_result = x if array[x] <= array[x - 1] else x - 1
else:
denom = array[x + 1] + array[x - 1] - 2 * array[x]
delta = array[x - 1] - array[x + 1]
if denom == 0:
return x
return x + delta / (2 * denom)
return x_result
def yin_type1(sig, samplerate):
diff = difference_type1(sig)
cmnd = cumulative_mean_normalized_difference(diff)
tau = absolute_threshold(cmnd)
if tau is None:
return numpy.nan
return samplerate / parabolic_interpolation(cmnd, tau)
def yin_type2(sig, samplerate):
diff = difference_type2(sig)
cmnd = cumulative_mean_normalized_difference(diff)
tau = absolute_threshold(cmnd)
if tau is None:
return numpy.nan
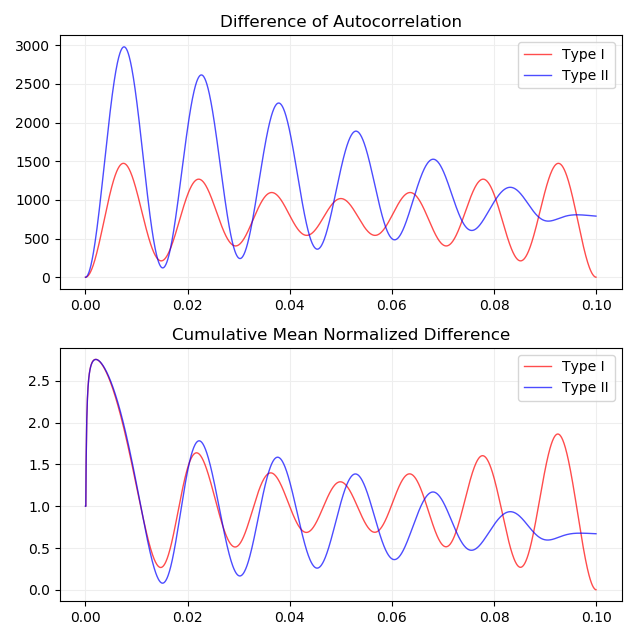
return samplerate / parabolic_interpolation(cmnd, tau)66Hz、0.1秒のサイン波の cumulative mean normalized difference の局所最小点のプロットです。横軸は時間で縦軸は信号の大きさです。推定したピッチは type I で 67.9Hz 、 type II で 66.3Hz となりました。
McLeod Pitch Method (MPM) は type II の自己相関関数を使ったYINの変形です。
処理の流れは次のようになります。
MPM の square difference function はYINの difference function と同じです。
\[ \begin{alignedat}{3} d[\tau] &= \sum_{j=0}^{N-1} (x[j] - x[j + \tau])^2 &&= 2 (r[0] - r[\tau]) &&\qquad\text{Type I}\\ d'[\tau] &= \sum_{j=0}^{N-\tau-1} (x[j] - x[j + \tau])^2 &&= r'[0] + r'_\tau[0] - 2r[\tau] &&\qquad\text{Type II} \end{alignedat} \]
MPMの論文では type II に注目して \(m'[\tau] = r'[0] + r'_{\tau}[0]\) と置き換えています。
\[ \begin{aligned} d'[\tau] &= m'[\tau] - 2r'[\tau]\\ m'[\tau] &= \sum_{j=0}^{N-\tau-1} (x^2[j] + x^2[j + \tau])\\ &= r'[0] + r'_{\tau}[0]\\ &= r'[0] + \sum_{j=\tau}^{N - 1} x^2[j] \end{aligned} \]
Type II の normalized square difference function は次のように定義されています。
\[ n'[\tau] = 1 - \frac{m'[\tau] - 2r'[\tau]}{m'[\tau]} = \frac{2r'[\tau]}{m'[\tau]} \]
Type I の normalized square difference function を考えてみます。
\[ \begin{aligned} m[\tau] &= 2r[0]\\ n[\tau] &= \frac{2r[\tau]}{m[\tau]} = \frac{r[\tau]}{r[0]} \end{aligned} \]
実装します。
def normalized_square_difference_type1(sig):
corr = autocorrelation_type1(sig)
return corr / corr[0] if corr[0] != 0 else corr
def normalized_square_difference_type2(sig):
corr = autocorrelation_type2(sig)
cumsum = (sig * sig)[::-1].cumsum()[::-1]
cumsum[cumsum < 1] = 1 # 発散を防ぐ。
return corr / (corr[0] + cumsum) # 後で値の比率しか使わないので係数2を省略。MPM では normalized square difference の局所最大点を探索します。 MPM での局所最大点とは、負から正になる一つのゼロクロス点と、それに続く正から負になるゼロクロス点の間の区間で、信号が最大になる点のことをいいます。
以下は探索の手順です。
実装します。
MPM_K = 0.5 # Type I NSD では後半に大きなピークができるので小さめに設定。
def estimate_period(diff):
start = 0
while diff[start] > 0:
start += 1
if start >= len(diff):
return None
threshold = MPM_K * numpy.max(diff[start:])
isNegative = True
max_index = None
for i in range(start, len(diff)):
if isNegative:
if diff[i] < 0:
continue
max_index = i
isNegative = False
if diff[i] < 0:
isNegative = True
if diff[max_index] >= threshold:
return max_index
if diff[i] > diff[max_index]:
max_index = i
return None
def mpm_type1(data, samplerate):
nsd = normalized_square_difference_type1(data)
index = get_period(nsd)
if index is None:
return numpy.nan
return samplerate / parabolic_interpolation(nsd, index)
def mpm_type2(data, samplerate):
nsd = normalized_square_difference_type2(data)
index = get_period(nsd)
if index is None:
return numpy.nan
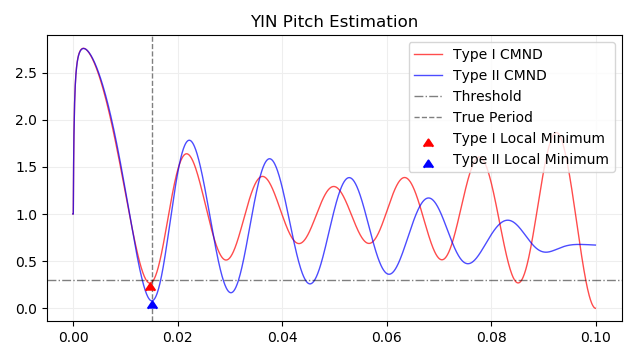
return samplerate / parabolic_interpolation(nsd, index)66Hz、0.1秒のサイン波と、その normalized square difference の局所最大点のプロットです。横軸は時間で縦軸は信号の大きさです。推定したピッチは type I で 67.5Hz 、 type II で 66.1Hz となりました。
8通りの手法の組み合わせが考えられます。名前が長いので cumulative mean normalized difference を CMND 、 normalized square difference を NSD と省略します。
| 周期の探索 | 差分関数 | 自己相関関数 | 備考 |
|---|---|---|---|
| YIN | CMND | Type I | オリジナルYIN |
| YIN | CMND | Type II | |
| YIN | NSD | Type I | |
| YIN | NSD | Type II | |
| MPM | CMND | Type I | |
| MPM | CMND | Type II | |
| MPM | NSD | Type I | |
| MPM | NSD | Type II | オリジナルMPM |
YIN の周期の探索でピッチを推定できるように NSD を加工します。
NSD では信号のピッチが局所最大点として表されていますが YIN の周期の探索では局所最小点を見つけます。そこでまずは NSD を反転します。
反転した NSD の最初に現れる局所最小点はインデックス0になります。そこで NSD のインデックス0から最初のゼロクロス点までの信号の値を0に置き換えます。
YIN の周期の探索で使うしきい値は0にします。 MPM のように負の最大値を探して適当な係数をかけたしきい値も使えそうですが、ここではパラメータを増やしたくなかったので定数にしました。
実装します。
def invert_nsd(nsd):
tau = 0
while nsd[tau] > 0:
nsd[tau] = 0
tau += 1
if tau >= len(nsd):
return None
return -nsd
def yin_nsd_type1(sig, samplerate):
nsd = normalized_square_difference_type1(sig)
nsd = invert_nsd(nsd)
if nsd is None:
return numpy.nan
tau = absolute_threshold(nsd, 0)
if tau is None:
return numpy.nan
return samplerate / tau
def yin_nsd_type2(sig, samplerate):
nsd = normalized_square_difference_type2(sig)
nsd = invert_nsd(nsd)
if nsd is None:
return numpy.nan
tau = absolute_threshold(nsd, 0)
if tau is None:
return numpy.nan
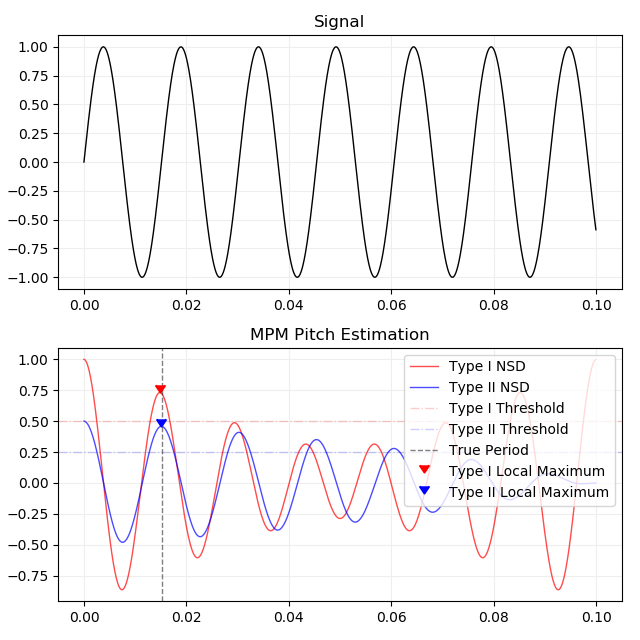
return samplerate / tauYIN-NSD で加工した NSD と局所最小点のプロットです。元の信号は66Hz、0.1秒のサイン波です。横軸は時間で縦軸は信号の大きさです。推定したピッチは type I で 67.5Hz 、 type II で 66.1Hz となりました。
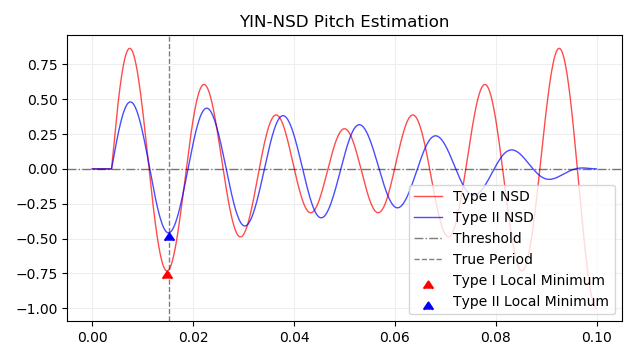
MPM の周期の探索でピッチを推定できるように CMND を加工します。
CMND では信号のピッチが局所最小点として表されていますが MPM の周期の探索では局所最大点を見つけます。そこでまずは CMND を反転します。
CMND の値はすべて0以上ですが MPM の周期の探索ではゼロクロス点が必要です。そこで反転した CMND に、反転する前の CMND の最大値の半分の値を足します。
実装します。
def mpm_cmnd_type1(sig, samplerate):
diff = difference_type1(sig)
cmnd = cumulative_mean_normalized_difference(diff)
cmnd = numpy.max(cmnd) / 2 - cmnd
index = estimate_period(cmnd)
if index is None:
return numpy.nan
return samplerate / parabolic_interpolation(cmnd, index)
def mpm_cmnd_type2(sig, samplerate):
diff = difference_type2(sig)
cmnd = cumulative_mean_normalized_difference(diff)
cmnd = numpy.max(cmnd) / 2 - cmnd
index = estimate_period(cmnd)
if index is None:
return numpy.nan
return samplerate / parabolic_interpolation(cmnd, index)MPM-CMND で加工した CMND と局所最大点のプロットです。元の信号は66Hz、0.1秒のサイン波です。横軸は時間で縦軸は信号の大きさです。推定したピッチは type I で 67.9Hz 、 type II で 66.3Hz となりました。
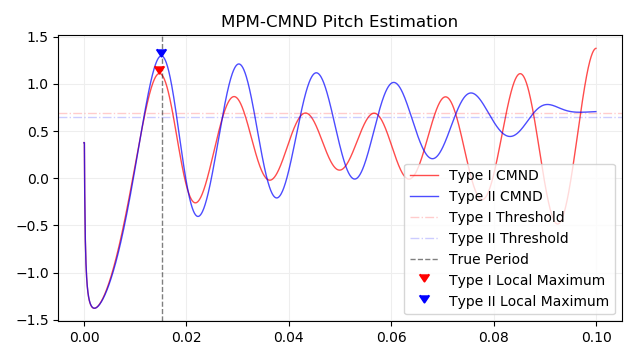
ここまでは一つの信号から一つのピッチを推定していました。ここから行うピッチ推定の評価では一つの信号を複数のフレームに分割して、それぞれのフレームから一つずつピッチを推定します。
実装では python_speech_features.sigproc.framesig
を使っています。フレームはオーバーラップすることがあります。信号の長さを超えることはありません。
def pitch_frame(data, samplerate, winlen, winstep, pitch_func=yin_cmnd_type2):
frame = python_speech_features.sigproc.framesig(
data,
frame_len=int(samplerate * winlen),
frame_step=int(samplerate * winstep),
)
return numpy.array([pitch_func(sig, samplerate) for sig in frame])真のピッチと比較できるときは周波数をセント値に変換して平均絶対誤差を計算します。
def hz_to_cent(frequency):
return 1200 * numpy.log2(frequency / 440)
def mean_absolute_error(true_value, data_value):
return numpy.nanmean(numpy.abs(true_value - data_value))
# 例。
true_cent = hz_to_cent(true_value)
data_cent = hz_to_cent(data)
mae = mean_absolute_error(true_cent, data_cent)周波数が一定のサイン波を入力信号としたときの平均絶対誤差です。
サイン波は次の条件で生成しました。
def generate_sin(duration, samplerate, frequency):
length = int(duration * samplerate)
phase = numpy.linspace(0, 2 * numpy.pi * frequency * duration, length)
return numpy.sin(phase)
def test_sin_wave(samplerate, duration, winlen, winstep, freq_low, freq_high,
num):
frequency = numpy.geomspace(freq_low, freq_high, num)
signals = [generate_sin(duration, samplerate, freq) for freq in frequency]
# signals からピッチを推定して誤差を計算。
samplerate = 16000 # サンプリング周波数 [Hz]
duration = 0.2 # 長さ [sec]
num = 32 # 誤差を求める信号の数
winlen = 0.1 # フレームの長さ [sec]
winstep = 0.01 # フレームの間隔 [sec]
freq_low = 10 # 最も低い周波数 [Hz]
freq_high = 8000 # 最も高い周波数 [Hz]
test_sin_wave(samplerate, duration, winlen, winstep, freq_low, freq_high, num)手法ごとの平均絶対誤差です。
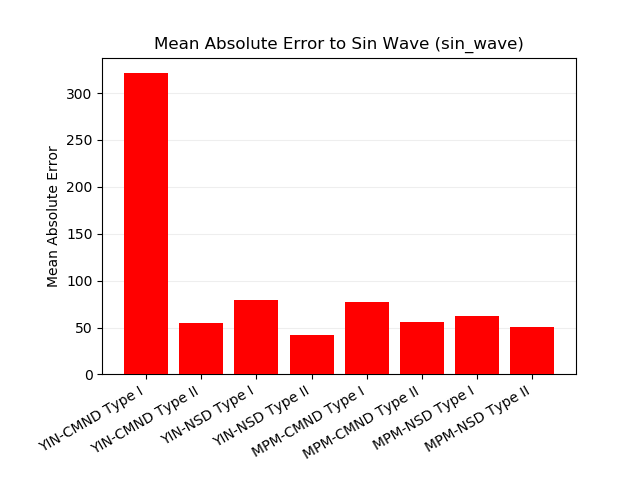
この他に作ったプロットは別ページにまとめました。
誤差が最小となったのは YIN-NSD type II です。
YIN-CMND type I は低周波域での誤差が大きく、全体の平均を押し上げています。
全体的に type I よりも type II のほうが誤差が低くなっています。
サイン波にノイズを加えたときでもピッチが推定できるか試します。
def generate_sin_with_noise(duration, samplerate, frequency, noise_ratio):
length = int(duration * samplerate)
phase = numpy.linspace(0, 2 * numpy.pi * frequency * duration, length)
signal = numpy.sin(phase) + noise_ratio * numpy.random.uniform(-1, 1)
return signal / (noise_ratio + 1)パラメータです。
samplerate = 16000
duration = 0.8
num = 32 # 32の周波数 * 32のノイズの比率 = 1024サンプル
winlen = 0.1
winstep = 0.01
freq_low = 10
freq_high = 8000
ratio_low = 0.01 # 最も小さいノイズの比率
ratio_high = 100 # 最も大きいノイズの比率
"""
ノイズの比率は次のように設定。
for ratio in numpy.geomspace(freq_low, freq_high, num):
signal = (sin_wave + ratio * noise) / (ratio + 1)
"""手法ごとの平均絶対誤差です。
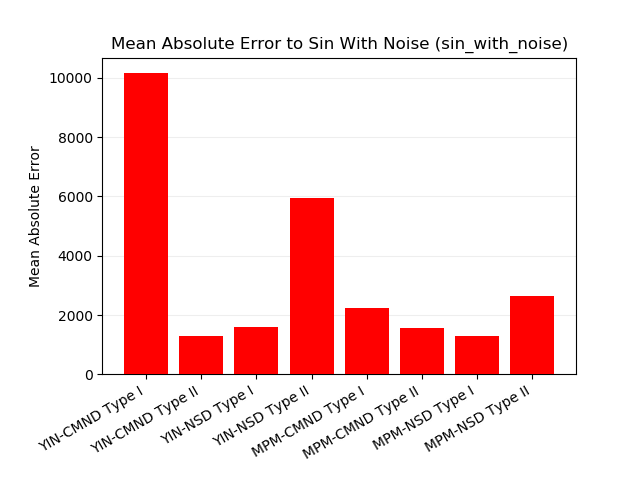
この他に作ったプロットは別ページにまとめました。
CMND type I の手法はノイズの比率が大きくなっても nan
が出ませんが誤差は大きめです。
NSD type II の手法はノイズの比率が3より大きいときに出る大きな誤差に引きずられて、全体の平均も悪くなっています。
それ以外の手法ではノイズの比率が大きいときでは nan
が出ますが NSD type II
のように全体の平均を大きく変えるような誤差は出ていません。
信号は次のように生成しました。
def generate_sin_am(duration, samplerate, car_freq, mod_freq):
length = int(duration * samplerate)
car_phase = numpy.linspace(0, 2 * numpy.pi * car_freq * duration, length)
mod_phase = numpy.linspace(0, 2 * numpy.pi * mod_freq * duration, length)
return numpy.sin(car_phase) * numpy.sin(mod_phase)
def generate_sin_fm(duration, samplerate, car_freq, mod_freq):
length = int(duration * samplerate)
mod_phase = numpy.linspace(0, 2 * numpy.pi * mod_freq * duration, length)
car_phase = numpy.full(length, 2 * numpy.pi * car_freq * duration / length)
phase = (car_phase + numpy.sin(mod_phase)).cumsum()
return numpy.sin(phase)パラメータです。
samplerate = 16000
duration = 0.8
num = 32 # 32のキャリア周波数 * 32のモジュレータ周波数 = 1024サンプル
winlen = 0.1
winstep = 0.01
car_freq_low = 10 # 最も小さいキャリアの周波数
car_freq_high = 8000 # 最も大きいキャリアの周波数
mod_freq_low = 0.1 # 最も小さいモジュレータの周波数
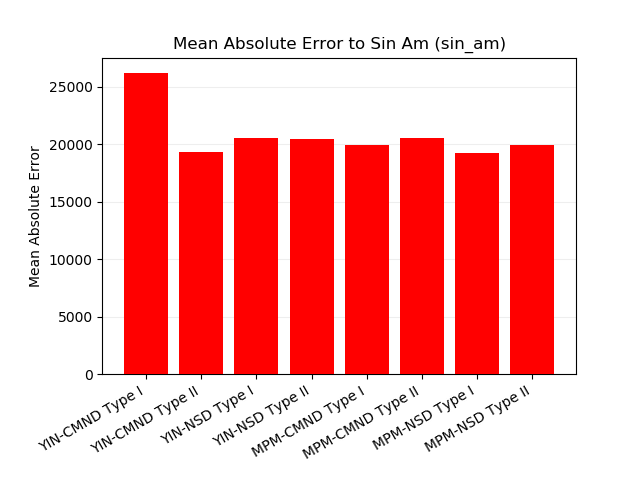
mod_freq_high = 800 # 最も大きいモジュレータの周波数AM変調をかけたサイン波に対する平均絶対誤差です。
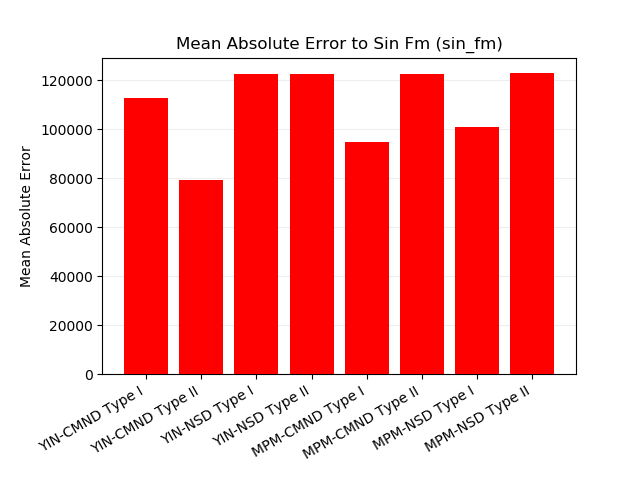
FM変調をかけたサイン波に対する平均絶対誤差です。
この他に作ったプロットは別ページにまとめました。
誤差からはどう間違っているかがわからないので、推定されたピッチを動画にしました。
AM変調をかけたサイン波から推定されたピッチです。
FM変調をかけたサイン波から推定されたピッチです。
評価が適当なので、この手法がいいというはっきりした結果は出ませんでした。
YIN-CMND type I はピッチの推定に失敗するとフレームの長さと同じ周期を推定する癖があるようです。
YIN-CMND type II 、 MPM-CMND type I 、 MPM-CMND type II はフレーム内のピッチが低いか変化が激しいときに推定に失敗するようです。3つの中では MPM-CMND type II が推定に失敗することが少ないように見えます。
YIN-NSD type I と YIN-NSD type II は適当に設定したしきい値のおかげで、どんな状況でも何らかのピッチを推定しています。ピッチが高めに推定されるのは YIN の周期の探索が原因だと思われます。
MPM-NSD type II は YIN-NSD type I と YIN-NSD type II よりも低周波域での推定に失敗しやすいようですが、ピッチが高めに推定されることが少ないように見えます。
MPM-NSD type I は動画では目立たかなったので特徴がつかめませんでした。
条件の良いときは CMND type II の誤差がもっとも少なくなります。クラスタリングの特徴としてはとりあえずこれを使うことにします。
実用的なピッチ推定については YIN-NSD type II か MPM-NSD type II がいいと思います。入力信号のフィルタリング、 NSD に窓をかける、しきい値や定数 \(k\) の調整といったところで改善が見込めます。