何かあれば GitHub のリポジトリに issue を作るか ryukau@gmail.com までお気軽にどうぞ。
Update: 2025-01-07
指数曲線 (Exponential Curve) を使ったエンベロープを作ります。
値が 1 から 0 に向かって減衰する指数曲線 \(E_d(t)\) の式です。
\[ E_d(t) = \alpha^t, \quad 0 \leq \alpha \leq 1. \]
\(\alpha\) は減衰の速さを決める任意の値、 \(t\) は単位が秒数の時間です。
ユーザから指定された減衰時間 \(\tau\) から \(\alpha\) を決めます。 \(E_d\) は \(0 < \alpha\) のとき \(t = +\infty\) でようやく 0 になります。言い換えると \(E_d\) はいつまで経っても 0 になりません。そこで 0 の代わりに十分に小さな値 \(\epsilon\) に到達する時間を求めます。
\[ E_d(\tau) = \alpha^\tau = \epsilon. \]
時間の単位を秒数 \(\tau\) からサンプル数 \(n_\tau\) に置き換えます。
\[ n_\tau = \tau f_s. \]
\(f_s\) はサンプリング周波数です。
\(\tau\) と \(\epsilon\) が与えられたとき \(\alpha^\tau = \epsilon\) の関係と \(n_\tau\) の式より \(\alpha\) が求められます。
\[ \alpha = \epsilon^\eta, \quad \eta = \frac{1}{\tau f_s}. \]
\(\epsilon\)
の値は任意です。この文章では 1e-5
を使っています。値を決めるときの参考までに、 10 進数では
float は約 7 桁、 double は約 16
桁の精度があります。
実装します。
#include <cmath>
template<typename Sample> class ExpDecayCurve {
public:
void reset(Sample sampleRate, Sample seconds)
{
value = Sample(1);
set(sampleRate, seconds);
}
void set(Sample sampleRate, Sample seconds)
{
alpha = pow(threshold, Sample(1) / (seconds * sampleRate));
}
bool isTerminated() { return value <= threshold; }
Sample process()
{
if (value <= threshold) return Sample(0);
value *= alpha;
return value - threshold;
}
protected:
const Sample threshold = 1e-5;
Sample value = 0;
Sample alpha = 0;
};reset() は再トリガ時、 set()
はコントロールレートで呼び出されます。
isTerminated() は複数の曲線を組み合わせて ADSR
エンベロープなどを作るとき、状態遷移を行うために使います。
process() の最後で threshold
を引いているのは、エンベロープの終端の不連続点を小さくするためです。この処理によって出力の範囲は
[0, 1 - threshold] になります。
値の範囲が [0, 1]
かつ終端に崖を作りたくないときはルックアップテーブルが使えます。ただし、滑らかさは劣ります。
増加する指数曲線 \(E_a(t)\) の式です。
\[ E_d(\tau) = \epsilon \alpha^\tau = 1. \]
\(\alpha\) について解きます。
\[ \alpha = \left( \frac{1}{\epsilon} \right)^\eta, \quad \eta = \frac{1}{\tau f_s}. \]
実装します。
template<typename Sample> class ExpAttackCurve {
public:
void reset(Sample sampleRate, Sample seconds)
{
value = threshold;
set(sampleRate, seconds);
}
void set(Sample sampleRate, Sample seconds)
{
alpha
= pow(Sample(1) / threshold, Sample(1) / (seconds * sampleRate));
}
bool isTerminated() { return value >= Sample(1); }
Sample process()
{
value *= alpha;
if (value >= Sample(1)) return Sample(1 - threshold);
return value - threshold;
}
protected:
const Sample threshold = 1e-5;
Sample value = 0;
Sample alpha = 0;
};\(1 - E_d(t)\) として減衰する指数曲線を上下反転して使う方法があります。
実装です。
// 1 - ExpDecayCurve.process();
template<typename Sample> class NegativeExpAttackCurve {
public:
void reset(Sample sampleRate, Sample seconds)
{
value = Sample(1);
set(sampleRate, seconds);
}
void set(Sample sampleRate, Sample seconds)
{
alpha = pow(threshold, Sample(1) / (seconds * sampleRate));
}
bool isTerminated() { return value <= threshold; }
Sample process()
{
if (value <= threshold) return Sample(1 - threshold);
value *= alpha;
return Sample(1 - threshold) - value;
}
protected:
const Sample threshold = 1e-5;
Sample value = 0;
Sample alpha = 0;
};C++ での実装例です。
このエンベロープは IterativeSinCluster
で使われています。この文章に掲載している実装では sustain
をバッファ内で補間していないので、サステイン中にサステイン音量を変更するとノイズが乗ります。また、エンベロープが終了していない状態で再トリガすると、デクリックの副エンベロープが掛け合わされることによってノイズが乗ります。
reset() の curve の値で
ExpAttackCurve と NegativeExpAttackCurve
を入れ替えられるようにしています。 curve
の値はトリガ時に渡された値をエンベロープの終了までに使い続けることを想定しています。
#include <algorithm>
#include <cmath>
// t in [0, 1].
template<typename Sample> inline Sample cosinterp(Sample t)
{
return 0.5 * (1.0 - cos(pi * t));
}
template<typename Sample> class ExpADSREnvelope {
public:
void setup(Sample sampleRate)
{
this->sampleRate = sampleRate;
declickLength = int32_t(0.001 * sampleRate);
}
Sample adaptTime(Sample seconds, Sample noteFreq)
{
const Sample cycle = Sample(1) / noteFreq;
return seconds < cycle ? cycle : seconds;
}
void reset(
Sample attackTime,
Sample decayTime,
Sample sustainLevel,
Sample releaseTime,
Sample noteFreq,
Sample curve)
{
if (declickCounter >= declickLength || state == State::terminated) declickCounter = 0;
state = State::attack;
sustain = std::clamp<Sample>(sustainLevel, Sample(0), Sample(1));
offset = value;
range = Sample(1) - value;
this->curve = std::clamp<Sample>(curve, Sample(0), Sample(1));
attackTime = adaptTime(attackTime, noteFreq);
atk.reset(sampleRate, attackTime);
atkNeg.reset(sampleRate, attackTime);
dec.reset(sampleRate, decayTime);
rel.reset(sampleRate, adaptTime(releaseTime, noteFreq));
}
void set(
Sample attackTime,
Sample decayTime,
Sample sustainLevel,
Sample releaseTime,
Sample noteFreq)
{
switch (state) {
case State::attack:
attackTime = adaptTime(attackTime, noteFreq);
atk.set(sampleRate, attackTime);
atkNeg.set(sampleRate, attackTime);
// Fall through.
case State::decay:
dec.set(sampleRate, decayTime);
// Fall through.
case State::sustain:
sustain = std::clamp<Sample>(sustainLevel, Sample(0), Sample(1));
// Fall through.
case State::release:
rel.set(sampleRate, adaptTime(releaseTime, noteFreq));
// Fall through.
default:
break;
}
}
void release()
{
range = value;
state = State::release;
}
bool isAttacking() { return state == State::attack; }
bool isReleasing() { return state == State::release; }
bool isTerminated() { return state == State::terminated; }
inline Sample declickIn(Sample input)
{
if (declickCounter >= declickLength) return input;
declickCounter += 1;
return input * cosinterp<Sample>(declickCounter / Sample(declickLength));
}
Sample process()
{
switch (state) {
case State::attack: {
const auto atkPos = atk.process();
const auto atkMix = atkPos + curve * (atkNeg.process() - atkPos);
value = range * declickIn(atkMix) + offset;
if (atk.isTerminated()) {
state = State::decay;
range = Sample(1) - sustain;
}
} break;
case State::decay:
value = range * declickIn(dec.process()) + sustain;
if (value <= sustain) state = State::sustain;
break;
case State::sustain:
value = declickIn(sustain);
break;
case State::release:
value = range * declickIn(rel.process());
if (rel.isTerminated()) state = State::terminated;
break;
default:
return 0;
}
return value;
}
protected:
enum class State : int32_t { attack, decay, sustain, release, terminated };
int32_t declickLength;
int32_t declickCounter = 0;
ExpAttackCurve<Sample> atk{};
NegativeExpAttackCurve<Sample> atkNeg{};
ExpDecayCurve<Sample> dec{};
ExpDecayCurve<Sample> rel{};
State state = State::terminated;
Sample value = 0;
Sample curve = 0;
Sample sampleRate = 44100;
Sample offset = 0;
Sample range = 1;
Sample sustain = 1;
};テストに使ったコードへのリンクです。
テスト結果です。図の縦軸は振幅、横軸は秒数です。音のサンプルはエンベロープを 100 Hz のサイン波の音量に適用しています。
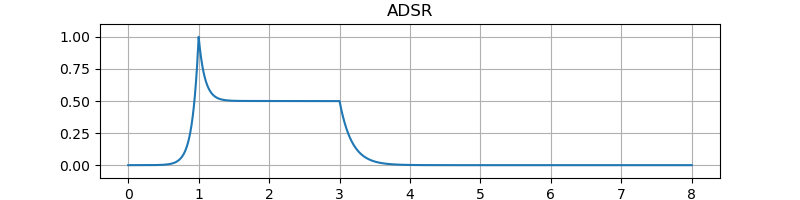
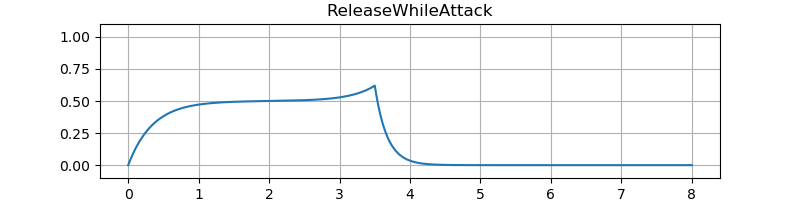
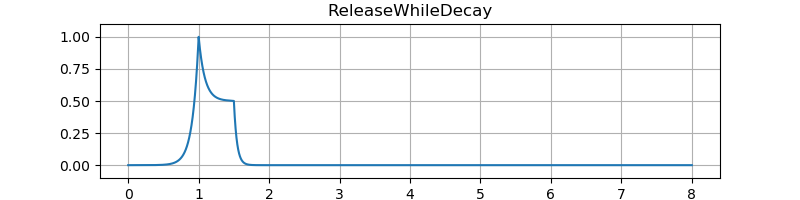
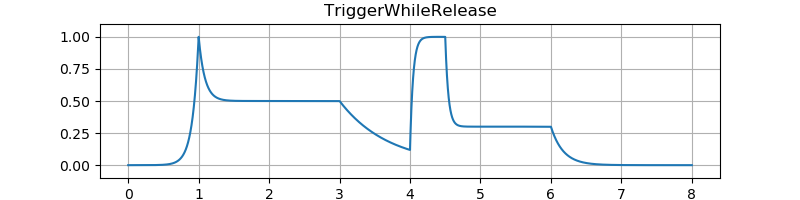
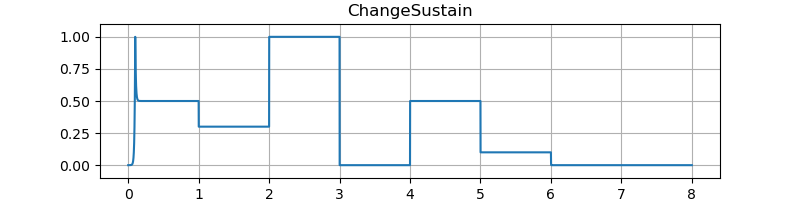
エンベロープのアタック時間やディケイ時間などがとても短いときにでるプチノイズを低減することをデクリック (declick) と呼びます。 Image-Line の Sytrus というシンセサイザでの用例にならっています。
ここでは 1
ミリ秒の短いアタックを持つ副エンベロープを用意して指数曲線を使った主エンベロープに掛け合わせています。また、直線の
ADSR エンベロープで紹介した adaptTime()
も組み合わせて使っています。
モノフォニックのときに副エンベロープを使うと再トリガの処理が複雑になるのでお勧めしません。出力を slew limiter に通すほうが楽に実装できます。オーディオプラグインの UI から入力された値の補間も参考にしてみてください。
図は副エンベロープによるデクリックを行ったエンベロープ出力の例です。副エンベロープのアタックカーブは \(0.5 + 0.5 \cos(n)\) で、 \(n\) は \(-\pi\) から \(0\) に向かって増加しています。
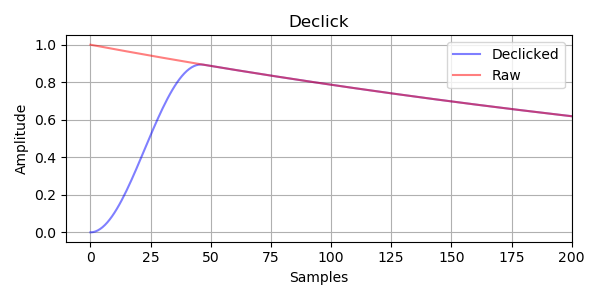
1000 Hz のサイン波の音量に適用した音のサンプルです。プチノイズが聞き取りやすいようにサイン波の初期位相を \(\dfrac{\pi}{2}\) にしています。
Exponential Moving Average (EMA) フィルタについてはオーディオプラグインの UI から入力された値の補間を参照してください。
ステップ状の不連続点を始点として指数曲線を描く出力が得られる EMA フィルタの特性を利用してエンベロープを実装します。
ユーザから指定された時間 \(T\) の逆数をカットオフ周波数 \(f_c\) に使っています。
\[ f_c = \frac{1}{T}. \]
アタックはカウンタを使って時間経過で次の状態に進みます。
リリースは出力がしきい値 threshold
以下になったときに次の状態に進みます。
状態 State::tail では出力が threshold
から 0 に到達するように直線を描きます。 threshold
をマシンイプシロンに固定するなら State::tail
は省略できます。
#include <algorithm>
#include <cmath>
#include <limits>
#include <numbers>
template<typename Sample> class EmaLowpass {
public:
// 原則として `double` で呼び出すこと。 `float` では精度が足りないので `timeInSamples`
// が 5000 を超えるあたりで正しい値が出ない。
static Sample samplesToP(Sample timeInSamples)
{
auto omega_c = std::numbers::pi_v<Sample> / timeInSamples;
auto y = Sample(1) - cos(omega_c);
return -y + sqrt((y + Sample(2)) * y);
}
void setP(Sample p) { kp = std::clamp<Sample>(p, Sample(0), Sample(1)); }
void reset(Sample value = 0) { this->value = value; }
Sample process(Sample input) { return value += kp * (input - value); }
Sample kp = 1; // Range in [0, 1].
Sample value = 0;
};
template<typename Sample> class ExpADSREnvelopeP {
public:
void setup(Sample sampleRate)
{
this->sampleRate = sampleRate;
tailLength = int(0.01 * sampleRate);
}
void reset(Sample attackTime, Sample decayTime, Sample sustainLevel, Sample releaseTime)
{
state = State::attack;
atk = int(sampleRate * attackTime);
decTime = decayTime;
sustain = std::clamp<Sample>(sustainLevel, Sample(0), Sample(1));
relTime = releaseTime;
lowpass.setP(EmaLowpass<double>::samplesToP(sampleRate * attackTime));
}
void set(Sample attackTime, Sample decayTime, Sample sustainLevel, Sample releaseTime)
{
switch (state) {
case State::attack:
atk = int(sampleRate * attackTime);
// Fall through.
case State::decay:
decTime = decayTime;
sustain = std::clamp<Sample>(sustainLevel, Sample(0), Sample(1));
// Fall through.
case State::release:
relTime = releaseTime;
default:
break;
}
if (state == State::attack)
lowpass.setP(EmaLowpass<double>::samplesToP(sampleRate * attackTime));
else if (state == State::decay)
lowpass.setP(EmaLowpass<double>::samplesToP(sampleRate * decayTime));
else if (state == State::release)
lowpass.setP(EmaLowpass<double>::samplesToP(sampleRate * releaseTime));
}
void release()
{
state = State::release;
lowpass.setP(EmaLowpass<double>::samplesToP(sampleRate * relTime));
}
bool isAttacking() { return state == State::attack; }
bool isReleasing() { return state == State::release; }
bool isTerminated() { return state == State::terminated; }
Sample process()
{
switch (state) {
case State::attack: {
value = lowpass.process(Sample(1));
--atk;
if (atk <= 0) {
state = State::decay;
lowpass.setP(EmaLowpass<double>::samplesToP(sampleRate * decTime));
}
} break;
case State::decay:
value = lowpass.process(sustain);
break;
case State::release:
value = lowpass.process(0);
if (value < threshold) {
value = threshold;
state = State::tail;
tailCounter = tailLength;
}
break;
case State::tail:
--tailCounter;
value = threshold * tailCounter / float(tailLength);
if (tailCounter <= 0) {
state = State::terminated;
lowpass.reset(0);
} else {
lowpass.reset(value);
}
break;
default:
return 0;
}
return value;
}
private:
enum class State { attack, decay, release, tail, terminated };
const Sample threshold = 1e-5;
int tailLength = 32;
int tailCounter = tailLength;
EmaLowpass<Sample> lowpass;
State state = State::terminated;
int atk = 0;
Sample decTime = 0;
Sample relTime = 0;
Sample sampleRate = 44100;
Sample sustain = 1;
Sample value = 0;
};テストに使ったコードへのリンクです。
テスト結果です。
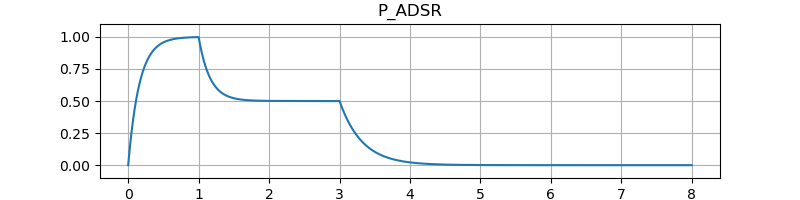
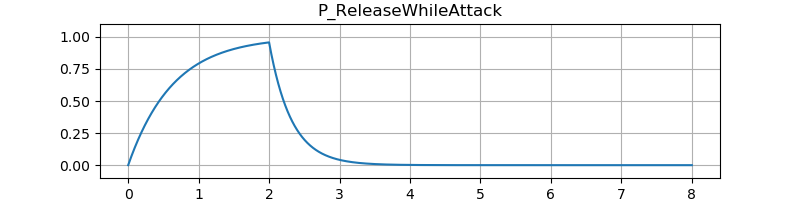
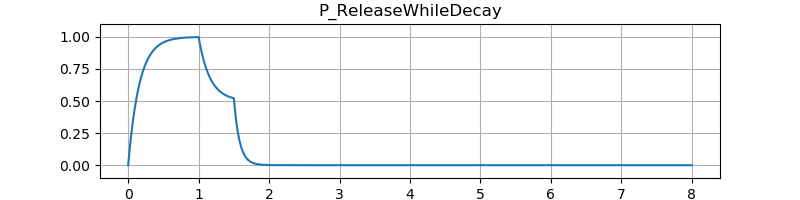
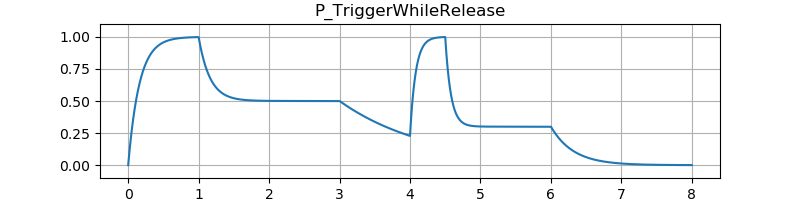
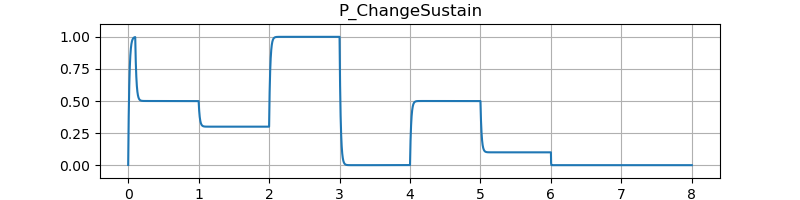
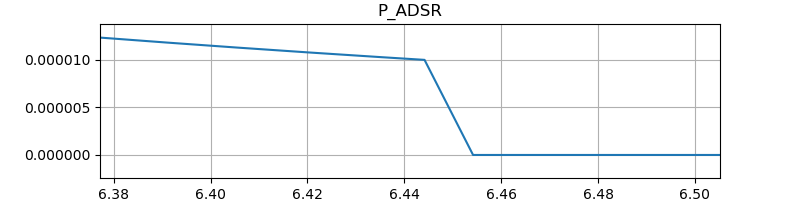
P_ADSR の State::tail
の部分を拡大した図です。
pow を使う形減衰する指数曲線とその反転を掛け合わせたエンベロープ \(E_{\mathtt{AD}}(t)\) を作ります。
\[ E_{\mathtt{AD}}(t) = (1 - a^{t}) d^{t}. \]
ピークの位置 \(t_p\) とピークの大きさ \(E_{\mathtt{AD}}(t_p)\) を求めます。 \(t_p\) はアタック時間です。 \(E_{\mathtt{AD}}(t_p)\) は出力範囲を \([0, 1]\) に正規化するために使えます。
\(t_p\) の時点で \(E_{\mathtt{AD}}(t)\) を \(t\) について微分した関数の値が 0 になるはずです。 Maxima で解きます。
expr: diff((1-a^t) * d^t, t);
solve(0 = expr, t);出力です。
\[ t_p = \frac{\log{\left( \dfrac{\log{(d)}}{\log{(d)}+\log{(a)}}\right) }}{\log{(a)}}. \]
\(a\) と \(d\) を求めます。ユーザが指定したアタック時間を \(A\) 、 ユーザが指定したディケイ時間を \(D\) とします。 \([0, 1)\) の範囲の適当なしきい値 \(\epsilon\) を用意して、 \(a^{A} = d^{D} = \epsilon\) とすると \(a, d\) は次の式で計算できます。
\[ a = \epsilon^{1/A}, \quad b = \epsilon^{1/D}. \]
エンベロープのプロットです。
実装を「C++
による実装」に掲載しています。 resetPow
に対応します。
exp を使う形この計算方法は EnvelopedSine
で使っています。 exp 、 log 、
log1p だけで実装できるので、 pow
を使う形よりも手軽です。
エンベロープ \(\tilde{E}_{\mathtt{AD}}\) の式です。
\[ \tilde{E}_{\mathtt{AD}}(t) = (1 - e^{at}) e^{dt}. \]
\(E_{\mathtt{AD}}(t)\) の式について \(a \to e^{a},\ d \to e^{d}\) と置き換えています。
ピークの位置 \(t_p\) とピークの大きさ \(\tilde{E}_{\mathtt{AD}}(t_p)\) を求めます。 SymPy を使います。
import sympy
def solveForExpPeakTime():
a = sympy.Symbol("a", real=True, negative=True)
d = sympy.Symbol("d", real=True, negative=True)
t = sympy.Symbol("t", real=True, positive=True)
E_diff1 = sympy.diff((1 - sympy.exp(a * t)) * sympy.exp(d * t), t)
solution = sympy.solve(E_diff1, t)
result = sympy.simplify(solution[0])
print(sympy.latex(result))整形した出力です。この形は log1p
が使えます。
\[ t_p = -\frac{\log{\left( \dfrac{a}{d}+1\right) }}{a}. \]
\(a\) と \(d\) を求めます。アタック時間を \(A\) 、 ディケイ時間を \(D\) 、 適当なしきい値を \(\epsilon \in [0, 1)\) とします。 \(e^{-a A},\ e^{-d D},\ \epsilon\) が等しくなるような \(a, d\) は次の式で計算できます。
\(e^{a A} = \epsilon\) より、
\[ a = \dfrac{\log(\epsilon)}{A}. \]
\(e^{d D} = \epsilon\) より、
\[ \begin{equation} d = \dfrac{\log(\epsilon)}{D}. \label{exp_d} \end{equation} \]
エンベロープのプロットです。出力は pow
を使う形と同じです。
実装を「C++
による実装」に掲載しています。 resetExp
に対応します。
エンベロープのピーク時間 \(t_p\) を直接指定できるように設計します。この形はパラメータの意味が大きく変わります。
exp を使う形の \(t_p\) の式を \(a\) について解きます。 \(t_p\) の式を再掲します。
\[ t_p = \frac{\log{\left( \dfrac{a}{d}+1\right) }}{a}. \]
SymPy で解きます。
import sympy
def solvePeakTimeForA():
a = sympy.Symbol("a", real=True, negative=True)
d = sympy.Symbol("d", real=True, negative=True)
t_p = sympy.Symbol("t_p", real=True, positive=True)
eq = sympy.Eq(t_p, -sympy.log(a / d + 1) / a)
solution = sympy.solve(eq, a)
result = sympy.simplify(solution[0])
print(sympy.latex(result))整形した出力です。 \(W_{-1}\) はブランチが -1 の Lambert W function です。
\[ a = \frac{W_{-1}\left(d t_{p} e^{d t_{p}}\right)}{t_{p}} - d. \]
これでアタック時間の設定ができました。ここからはディケイ時間の設定について調べます。 \(W_{-1}\) は以下の範囲でのみ定義されています。
\[ -\frac{1}{e} \leq d t_p e^{d t_p} < 0. \]
\(d t_p e^{d t_p}\) は、 \(d t_p \to -\infty\) のとき \(0\) 、 \(d t_p \to -1\) のとき \(-\dfrac{1}{e}\) 、となるので以下のように変形できます。
\[ -1 \geq d t_p > -\infty. \]
式 \(\ref{exp_d}\) を \(d\) に代入して \(D\) について解きます。
\[ \begin{aligned} -1 & \geq \dfrac{\log(\epsilon)}{D} t_p > -\infty, \\ -D & \geq \log(\epsilon) t_p > -\infty. \end{aligned} \]
\(D\) を以下のように設定すると \(W_{-1}\) の定義域でディケイ時間を設定できることがわかりました。
\[ D = \delta - \log(\epsilon) t_p, \quad \delta > 0. \]
\(\delta\) は減衰の長さを変えるリリース時間のようなパラメータですが、直感的には使えないことに注意してください。例えば \(t_p=3,\,\delta=1\) としたとき、エンベロープが十分に小さい値に到達するのは 4 秒後よりもずっと後になります。以下の式を \(t\) について解くことができればエンベロープが \(\epsilon\) に到達する具体的な時間が得られますが、 SymPy 、 Maxima 、 Wolfram Alpha では解けなかったです。
\[ \epsilon = (1 - e^{at}) e^{dt}. \]
エンベロープのプロットです。パラメータの意味が異なるので、出力も他の形とは異なります。以下のプロットは他の形の出力と似たような見た目になるようにパラメータを調整してあります。
実装を「C++
による実装」に掲載しています。 resetPeak
に対応します。
C++ で実装します。以下は完全な実装とテストコードへのリンクです。
Lambert W function は Darko Veberic さんによる実装を使っています。 Boost::math にも実装があります。
#include "lib/LambertW.hpp"
#include <algorithm>
#include <cmath>
#include <limits>
template<typename Sample> class ExpAD {
private:
Sample gain = 0;
Sample valueA = 0;
Sample alphaA = 0;
Sample valueD = 0;
Sample alphaD = 0;
public:
bool isTerminated() { return valueD <= std::numeric_limits<Sample>::epsilon(); }
void resetPow(Sample sampleRate, Sample attackSeconds, Sample decaySeconds)
{
constexpr Sample epsilon = Sample(1e-5);
valueA = Sample(1);
alphaA
= std::pow(epsilon, Sample(1) / std::max(Sample(1), attackSeconds * sampleRate));
valueD = Sample(1);
alphaD
= std::pow(epsilon, Sample(1) / std::max(Sample(1), decaySeconds * sampleRate));
const auto log_a = std::log(alphaA);
const auto log_d = std::log(alphaD);
const auto t_p = std::log(log_d / (log_a + log_d)) / log_a;
gain = Sample(1) / ((Sample(1) - std::pow(alphaA, t_p)) * std::pow(alphaD, t_p));
}
void resetExp(Sample sampleRate, Sample attackSeconds, Sample decaySeconds)
{
constexpr Sample epsilon = Sample(1e-5);
const auto a_ = std::log(epsilon) / attackSeconds;
const auto d_ = std::log(epsilon) / decaySeconds;
valueA = Sample(1);
alphaA = std::exp(a_ / sampleRate);
valueD = Sample(1);
alphaD = std::exp(d_ / sampleRate);
const auto t_p = -std::log1p(a_ / d_) / a_;
gain = Sample(1) / ((Sample(1) - std::exp(a_ * t_p)) * std::exp(d_ * t_p));
}
void resetPeak(Sample sampleRate, Sample peakSeconds, Sample releaseSeconds)
{
constexpr Sample epsilon = std::numeric_limits<Sample>::epsilon();
const auto decaySeconds = releaseSeconds - std::log(epsilon) * peakSeconds;
const auto d_ = std::log(epsilon) / decaySeconds;
const auto x_ = d_ * peakSeconds;
const auto a_ = Sample(utl::LambertW(-1, x_ * std::exp(x_))) / peakSeconds - d_;
const auto attackSeconds = -std::log(epsilon) / std::log(-a_);
valueA = Sample(1);
alphaA = std::exp(a_ / sampleRate);
valueD = Sample(1);
alphaD = std::exp(d_ / sampleRate);
gain = Sample(1)
/ ((Sample(1) - std::exp(a_ * peakSeconds)) * std::exp(d_ * peakSeconds));
}
Sample process()
{
valueA *= alphaA;
valueD *= alphaD;
return gain * (Sample(1) - valueA) * valueD;
}
};\Tau が MathJax で表示されていなかったので
\eta に置換。P Controller による実装 を追加。