何かあれば GitHub のリポジトリに issue を作るか ryukau@gmail.com までお気軽にどうぞ。
Update: 2025-01-07
2 重ばねの式から適当に係数などを入れ替えて次のコードを作りました。
class Model:
def __init__(self, k1, k2):
self.k1 = k1
self.k2 = k2
self.acc1 = 0
self.vel1 = 0
self.pos1 = 0
self.acc2 = 0
self.vel2 = 0
self.pos2 = 0
self.x1 = 0
def processLP(self, x0):
self.acc2 = self.k2 * (self.vel1 - self.vel2)
self.vel2 += self.acc2 + x0 - self.x1
self.pos2 += self.vel2 * self.k2
self.acc1 = -self.k1 * self.pos1 - self.acc2
self.vel1 += self.acc1
self.pos1 += self.vel1
self.x1 = x0
return self.pos2この文章では上のコードのフィルタのことを DoubleFilter と呼ぶことにします。
pos1 からはハイパス、 pos2
からはローパスに近い出力が出力が得られました。ローパスフィルタのほうが好きなので
pos2 について k1 と k2
をチューニングします。
k1 と k2
について次のことが知りたいです。
k1, k2 の値を決める式。k1, k2 の値を決める式。コードを式に直します。
\[ \begin{aligned} \ddot{u_2}[n] &= k_2 (\dot{u_1}[n-1] - \dot{u_2}[n-1]) \\ \dot{u_2}[n] &= \dot{u_2}[n-1] + \ddot{u_2}[n] + x[n] - x[n - 1] \\ u_2[n] &= u_2[n-1] + k_2 \dot{u_2}[n] \\ \\ \ddot{u_1}[n] &= -k_1 u_1[n-1] - \ddot{u_2}[n] \\ \dot{u_1}[n] &= \dot{u_1}[n-1] + \ddot{u_1}[n] \\ u_1[n] &= u_1[n-1] + \dot{u_1}[n] \\ \end{aligned} \]
\(u_2\) の項だけが残るようにフィルタの式を変形します。
\[ \begin{aligned} \dot{u_1}[n] &= \frac{1}{k_2} \ddot{u_2}[n+1] - \dot{u_2}[n] &(1) \\ \ddot{u_2}[n] &= \dot{u_2}[n] - \dot{u_2}[n-1] - x[n] + x[n-1] &(2) \\ \dot{u_2}[n] &= \frac{1}{k_2} (u_2[n] - u_2[n-1]) &(3) \\ \\ u_1[n] &= \frac{1}{k_1} \left( - \ddot{u_1}[n+1] - \ddot{u_2}[n+1] \right) &(4) \\ \ddot{u_1}[n] &= \dot{u_1}[n] - \dot{u_1}[n-1] &(5) \\ \dot{u_1}[n] &= u_1[n] - u_1[n-1] &(6)\\ \end{aligned} \]
次の手順で代入すると \(x\) と \(u_2\) の項だけの式になります。
Maxima で代入します。
d1_u1(n) := d2_u2(n + 1) / k_2 - d1_u2(n); /* (1) */
d2_u2(n) := d1_u2(n) - d1_u2(n - 1) - x(n) + x(n - 1); /* (2) */
d1_u2(n) := (u_2(n) - u_2(n - 1)) / k_2; /* (3) */
u_1(n) := (-d2_u1(n + 1) - d2_u2(n + 1)) / k_1; /* (4) */
d2_u1(n) := d1_u1(n) - d1_u1(n - 1); /* (5) */
result: d1_u1(n) = u_1(n) - u_1(n - 1); /* (6) */
ratvars(u(n), u(n-1), u(n-2), u(n-3), x(n), x(n-1), x(n-2), x(n-3));
ratexpand(0 = rhs(result) - lhs(result));出力に \(k_1 k_2\) を掛けて整理した式です。
\[ \begin{aligned} & x[n] \ +\ (k_2 + k_1 - 3) x[n-1] \ +\ (- 2 k_2 - k_1 + 3) x[n-2] \ +\ ( k_2 - 1) x[n-3] \\&\quad= \frac{1}{k_2} u_2[n] \ +\ \frac{k_1 - 4}{k_2} u_2[n-1] \ -\ \left( \frac{2 k_1 - 6}{k_2} + k_1 \right) u_2[n-2] \\&\qquad \ +\ \left( \frac{k_1 - 4}{k_2} + k_1 \right) u_2[n-3] \ +\ \frac{1}{k_2} u_2[n-4] \end{aligned} \]
伝達関数です。
\[ \begin{aligned} &H(z) = \frac{ b_0 + b_1 z^{-1} + b_2 z^{-2} + b_3 z^{-3} }{ a_0 + a_1 z^{-1} + a_2 z^{-2} + a_3 z^{-3} + a_4 z^{-4} } \\& \\& \begin{aligned} b_0 &= 1 \\ b_1 &= k_2 + k_1 - 3 \\ b_2 &= - 2 k_2 - k_1 + 3 \\ b_3 &= k_2 - 1 \\ \end{aligned} \qquad \qquad \begin{aligned} a_0 &= \frac{1}{k_2} \\ a_1 &= \frac{k_1 - 4}{k_2} \\ a_2 &= \frac{- 2 k_1 + 6}{k_2} - k_1 \\ a_3 &= \frac{k_1 - 4}{k_2} + k_1 \\ a_4 &= \frac{1}{k_2} \\ \end{aligned} \end{aligned} \]
次のコードは scipy.signal
で使える形にした伝達関数です。
def transferFunctionU2(k1, k2):
return (
[
1, # b0
k2 + k1 - 3, # b1
-2 * k2 - k1 + 3, # b2
k2 - 1, # b3
0, # b4 は無いので 0 。
],
[
1 / k2, # a0
(k1 - 4) / k2, # a1
(-2 * k1 + 6) / k2 - k1, # a2
(k1 - 4) / k2 + k1, # a3
1 / k2, # a4
],
)プロットに使ったコードは 3-pole ローパスフィルタ と同じなので省略します。
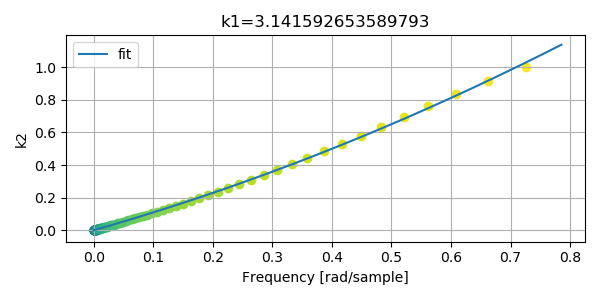
次の図は \(k_1\) を \(\pi\) に固定して \(k_2\) を動かしたときの振幅特性です。 \(k_1\) が \(\pi\) を超えても振幅特性は計算できますが、実際に信号を入力すると発散しました。 プロットの丸い点は -3 dB の位置です。

ローパスのような特性ですが、ナイキスト周波数の近くに変なピークがあります。 \(k_1\) を 0 に近づけるとピークの位置が 0 Hz に近づきます。
カットオフ周波数 \(\omega_c\) から
\(k_2\) を求める近似曲線を numpy.polyfit
を使って求めたところ、次の式が見つかりました。中点 \(\cdot\) は乗算を表しています。
\[ k_2 = 6.5451144600705975 \cdot x + 20.46391326872472 \cdot x^2, \qquad x = \frac{\omega_c}{2 \pi}. \]
\(k_2\) が 1.0
を超えると発散するので、 \(k_2\) が
1.0 を超えないようなカットオフ周波数の上限を探します。 Maxima の
solve を使います。 numer
は実数で結果を表示するオプションです。
solve(1 = 6.5451144600705975 * x + 20.46391326872472 * x^2, x), numer;\(k_2 = 1\) のときの \(x\) の値は 0.1129192677515388 になりました。サンプリング周波数 \(f_s\) に応じたカットオフ周波数の上限 \(f_u\) は次の式で計算できます。
\[ f_u = 0.1129192677515388 \cdot f_s \]
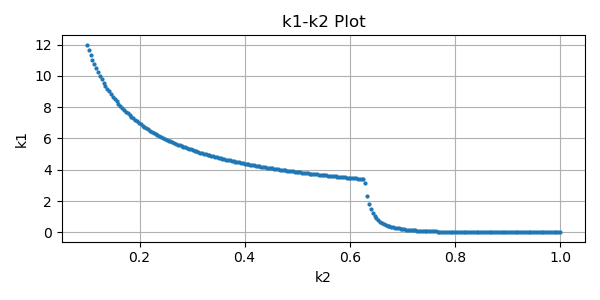
カットオフ周波数と近似曲線のプロットです。丸い点が振幅特性から求めたカットオフ周波数、青い線が近似曲線です。
\(k_2\) がユーザによって決められたときに発散しない \(k_1\) の最大値を探します。
scipy.signal.tf2zpk
から得られる伝達関数の極の絶対値の最大値が 1 になるような \(k_1\) の値を探します。
import numpy as np
import scipy.signal as signal
import matplotlib.pyplot as pyplot
def stabilityPlot(transferFunction):
maxIteration = 1024
nK2 = 256
data = []
for idx, k2 in enumerate(np.linspace(0.1, 1, nK2)):
k1 = 65536
delta = k1 / 2
jdx = 0
while jdx < maxIteration:
b, a = transferFunction(k1, k2)
_, pole, gain = signal.tf2zpk(b, a)
if np.max(np.abs(pole * gain)) >= 1:
k1 -= delta
else:
k1 += delta
jdx += 1
delta *= 0.5
data.append((k1, k2))
print(idx, k1, k2)
k1, k2 = zip(*data)
pyplot.scatter(k2, k1, s=4, zorder=2)
pyplot.grid(zorder=1)
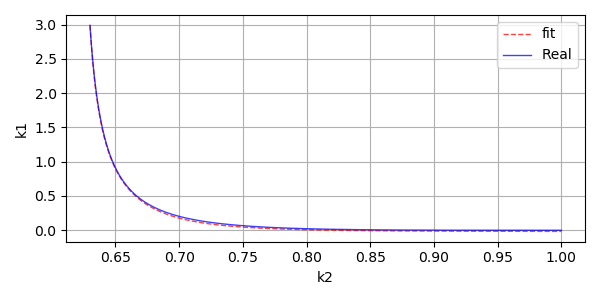
pyplot.show()出力されたプロットです。
\(k_2\) が 0.6 を超えたあたりで異なる曲線がつなぎ合わされているように見えます。曲線が変わる点での \(k_2\) の値を \(\xi_{k_2}\) とします。 \(\xi_{k_2}\) の値は \(2 \pi\) に近いですが、はっきりしないので近似曲線を探すときは 0.63 を使っています。
\(k_2\) が \(\xi_{k_2}\) 以下のときに対応する \(k_1\) をそのまま使うと発散しました。そこで \(k_2\) が \(\xi_{k_2}\) 以下のときは \(k_1\) の上限を \(\pi\) にします。
\(k_2\) が \(\xi_{k_2}\) 以上のときに \(k_2\) から \(k_1\)
を求める近似曲線を探します。いろいろ試したところ scipy.optimize.curve_fit
に次の関数を渡すと近似できました。
def curve_func(x, a0, a1, a2, a3, a4):
return 1 / (a0 + a1 * x + a2 * x * x + a3 * x * x * x + a4 * x * x * x * x)得られた近似曲線の式です。 \(C_0\) は \(k_2 = 0\) のとき \(k_1 = 0\) となるように調整しました。
\[ \begin{aligned} k_1 &\approx \begin{cases} \mathtt{resonance} \cdot \pi &, \quad k_2 < \xi_{k_2} \\ \mathtt{resonance} \cdot \left(C_0 + \dfrac{1}{C_1 + C_2 k_2 + C_3 (k_2)^2 + C_4 (k_2)^3 + C_5 (k_2)^4} \right) &, \quad \xi_{k_2} \leq k_2. \end{cases} \\ \\ C_0 &= -0.0049691265927442885\\ C_1 &= -471.738128187657\\ C_2 &= 1432.5662635997667\\ C_3 &= 345.2853784111966\\ C_4 &= -4454.40786711102\\ C_5 &= 3468.062963176107\\ \end{aligned} \]
近似曲線が \(k_2 = \xi_{k_2}\) のときに \(\pi\) となる \(\xi_{k_2}\) は \(0.6295160864148501\) です。
\(k_2 \geq \xi_{k_2}\) のときの実データと近似曲線のプロットです。
プラグインにして試したところ \(\mathtt{resonance} = 1\) かつ \(k_2\) が \(\xi_{k_2}\) より小さいときに発散することが分かりました。試行錯誤を重ねた結果、 \(k_1\) に 0.69 を掛け合わせると発散しなくなりました。次のようなコードで \(k_2 < \xi_{k_2}\) のときの \(k_1\) の値を小さくします。
def shelveK1(k1, k2):
k1Gain = 0.69
k1Delta = 0.31 # 1 - k1Gain.
B_2 = 0.63 # Tuning boundary (xi_{k_2}).
B_3 = 0.635
if k2 < B_2:
k1 *= k1Gain
elif k2 >= B_2 and k2 < B_3:
k1 *= k1Gain + k1Delta * (k2 - B_2) / (B_3 - B_2)
return k1最終的な \(k_1\) のチューニング曲線のプロットです。
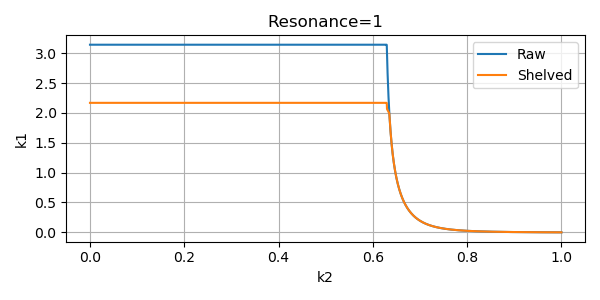
思いつきで sqrt(k1) を pos2
の式に掛け合わせて出力ゲインのチューニングを変えてみました。
import math
class Model:
# ...
def processLP(self, x0):
self.acc2 = self.k2 * (self.vel1 - self.vel2)
self.vel2 += self.acc2 + x0 - self.x1
self.pos2 += self.vel2 * self.k2 * math.sqrt(k1)
self.acc1 = -self.k1 * self.pos1 - self.acc2
self.vel1 += self.acc1
self.pos1 += self.vel1
self.x1 = x0
return self.pos2出力ゲインのチューニングを変えると \(k_1\) の上限が変わります。
\(k_1\) が \(0.7 \pi\) よりも大きいと発散するので、近似曲線から得られた値に 0.7 を掛け合わせます。
0.7 を掛け合わせても \(k_2\) が \(\xi_{k_2}\) より小さく \(\xi_{k_2}\) に近いときに発散します。そこで \(\xi_{k_2}\) の周りにチューニングの凹みを作ります。
def dentK1(k1, k2):
k1Gain = 0.69
k1Delta = 0.31 # 1 - k1Gain.
B_0 = 0.61
B_1 = 0.625
B_2 = 0.63 # Tuning boundary (xi_{k_2}).
B_3 = 0.635
if k2 >= B_0 and k2 < B_1:
k1 *= Sample(1) - k1Delta * (k2 - B_0) / (B_1 - B_0)
elif k2 >= B_1 and k2 < B_2:
k1 *= k1Gain
elif k2 >= B_2 and k2 < B_3:
k1 *= k1Gain + k1Delta * (k2 - B_2) / (B_3 - B_2)
return k1 * 0.7sqrt(k1) を pos2 の式に掛けたときの \(k_1\)
のチューニング曲線のプロットです。
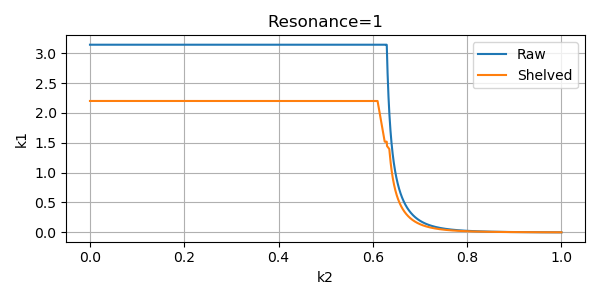
フィルタの式の \(u_1\) を出力に使うとハイパスフィルタを通したような音になります。出力 \(u_2\) のチューニングを使っても発散しなかったので流用することにしました。
C++ による実装です。
template<typename Sample> class DoubleFilter {
public:
void reset()
{
acc2 = vel2 = pos2 = 0;
acc1 = vel1 = pos1 = 0;
x1 = 0;
}
void set(Sample sampleRate, Sample cutoffHz, Sample resonance, bool altGain)
{
Sample x = cutoffHz / sampleRate;
k2 = Sample(6.5451144600705975) * x + Sample(20.46391326872472) * x * x;
// k2 ~= 0.2π (~0.63) のあたりにチューニングの境界がある。
if (k2 < Sample(0.6295160864148501)) {
k1 = Sample(pi) * resonance;
} else {
k1 = resonance
* (Sample(-0.0049691265927442885)
+ Sample(1)
/ (Sample(-471.738128187657) + Sample(1432.5662635997667) * k2 + Sample(345.2853784111966) * k2 * k2 + Sample(-4454.40786711102) * k2 * k2 * k2 + Sample(3468.062963176107) * k2 * k2 * k2 * k2));
}
const auto k1Gain = Sample(0.69);
const auto k1Delta = Sample(0.31); // 1 - k1Gain.
const auto B_0 = Sample(0.61);
const auto B_1 = Sample(0.625);
const auto B_2 = Sample(0.63); // だいたいチューニング境界。
const auto B_3 = Sample(0.635);
if (altGain) {
// k2 の値が チューニング境界 (~0.63) に近いときに k1 を小さくする。
if (k2 >= B_0 && k2 < B_1)
k1 *= Sample(1) - k1Delta * (k2 - B_0) / (B_1 - B_0);
else if (k2 >= B_1 && k2 < B_2)
k1 *= k1Gain;
else if (k2 >= B_2 && k2 < B_3)
k1 *= k1Gain + k1Delta * (k2 - B_2) / (B_3 - B_2);
k1 *= Sample(0.7);
v2Gain = somesqrt<Sample>(k1);
} else {
// k2 の値が チューニング境界 (~0.63) より小さいときに k1 を小さくする。
if (k2 < B_2)
k1 *= k1Gain;
else if (k2 >= B_2 && k2 < B_3)
k1 *= k1Gain + k1Delta * (k2 - B_2) / (B_3 - B_2);
v2Gain = Sample(1);
}
}
Sample process(Sample x0, bool highpass)
{
acc2 = k2 * (vel1 - vel2);
vel2 += acc2 + x0 - x1;
pos2 += vel2 * k2 * v2Gain;
acc1 = -k1 * pos1 - acc2;
vel1 += acc1;
pos1 += vel1;
x1 = x0;
// 直流除去のため 0.999 を掛け合わせる。
if (highpass) return pos1 *= Sample(0.999);
return pos2 *= Sample(0.999);
}
private:
Sample k1 = 0;
Sample k2 = 0;
Sample v2Gain = 1;
Sample acc2 = 0;
Sample vel2 = 0;
Sample pos2 = 0;
Sample acc1 = 0;
Sample vel1 = 0;
Sample pos1 = 0;
Sample x1 = 0;
};サンプルの生成に使ったコードへのリンクです。
カットオフ周波数の変調には numpy.geomspace
を使っています。
cutoff = 5000 * numpy.geomspace(1e-5, 1, nSample)入力信号は scipy.signal.sawtooth
で生成した 45 Hz ののこぎり波です。
altGain が true のとき sqrt(k1) を
pos2 に掛け合わせています。
altGain = False としたときの出力です。
altGain = True としたときの出力です。
altGain = False としたときの出力です。
altGain = True としたときの出力です。
フィルタの式を再掲します。
\[ \begin{aligned} \ddot{u_2}[n] &= k_2 (\dot{u_1}[n-1] - \dot{u_2}[n-1]) \\ \dot{u_2}[n] &= \dot{u_2}[n-1] + \ddot{u_2}[n] + x[n] - x[n - 1] \\ u_2[n] &= u_2[n-1] + k_2 \dot{u_2}[n] \\ \\ \ddot{u_1}[n] &= -k_1 u_1[n-1] - \ddot{u_2}[n] \\ \dot{u_1}[n] &= \dot{u_1}[n-1] + \ddot{u_1}[n] \\ u_1[n] &= u_1[n-1] + \dot{u_1}[n] \\ \end{aligned} \]
\(u_1\) の項だけが残るようにフィルタの式を変形します。
\[ \begin{aligned} \dot{u_2}[n] &= \dot{u_1}[n] - \frac{1}{k_2} \ddot{u_2}[n+1] &(1) \\ \ddot{u_2}[n] &= \dot{u_2}[n] - \dot{u_2}[n-1] - x[n] + x[n - 1] &(2) \\ \\ \ddot{u_2}[n] &= - \ddot{u_1}[n] - k_1 u_1[n-1] &(3) \\ \ddot{u_1}[n] &= \dot{u_1}[n] - \dot{u_1}[n-1] &(4) \\ \dot{u_1}[n] &= u_1[n] - u_1[n-1] &(5) \\ \end{aligned} \]
次の手順で代入して \(u_1\) の項だけにします。
d1_u2(n) := d1_u1(n) - d2_u2(n + 1) / k_2; /* (1) */
d2_u2(n) := -d2_u1(n) - k_1 * u_1(n - 1); /* (3) */
d2_u1(n) := d1_u1(n) - d1_u1(n - 1); /* (4) */
d1_u1(n) := u_1(n) - u_1(n - 1); /* (5) */
result: d2_u2(n) = d1_u2(n) - d1_u2(n - 1) - x(n) + x(n - 1); /* (2) */
ratvars(u(n), u(n-1), u(n-2), u(n-3), x(n), x(n-1), x(n-2), x(n-3));
ratexpand(0 = rhs(result) - lhs(result));出力です。
\[ \begin{aligned} 0=& - x(n) \\& + x(n-1) \\& + \frac{u_1(n+1)}{k_2} \\& + \frac{k_1 u_1(n)}{k_2} - \frac{3 u_1(n)}{k_2} + 2 u_1(n) \\& - \frac{k_1 u_1(n-1)}{k_2} + \frac{3 u_1(n-1)}{k_2} + k_1 u_1(n-1) - 4 u_1(n-1) \\& - \frac{u_1(n-2)}{k_2} + 2 u_1(n-2) \end{aligned} \]
整理します。
\[ \begin{aligned} x[n-1] - x[n-2] =& \frac{1}{k_2} u_1[n] + \left( \frac{k_1 - 3}{k_2} + 2 \right) u_1[n-1] \\& + \left( \frac{- k_1 + 3}{k_2} + k_1 - 4 \right) u_1[n-2] + \left( \frac{- 1}{k_2} + 2 \right) u_1[n-3] \end{aligned} \]
伝達関数が得られました。
\[ H(z) = \frac{z^{-1} - z^{-2}}{C_0 + C_1 z^{-1} + C_2 z^{-2} + C_3 z^{-3}} ,\qquad \begin{aligned} C_0 &= \frac{1}{k_2} \\ C_1 &= \frac{k_1 - 3}{k_2} + 2 \\ C_2 &= \frac{- k_1 + 3}{k_2} + k_1 - 4 \\ C_3 &= \frac{- 1}{k_2} + 2 \\ \end{aligned} \]