何かあれば GitHub のリポジトリに issue を作るか ryukau@gmail.com までお気軽にどうぞ。
Update: 2025-01-07
ばねとダンパの項を含んだ加速度の式がフィルタになりそうだと思いました。
\[ \ddot{u} = c \dot{u} + k u \]
\(c\) はダンピング係数、 \(k\) はばね係数です。
\(\ddot{u}\) の式から試行錯誤して以下の式を見つけました。
\[ \begin{aligned} \ddot{u} =& c \dot{u} + k \ddot{u} \\ \dot{u} \mathrel{{-}{=}}& \ddot{u} + V[n] \\ u \mathrel{{-}{=}}& \frac{c}{1 - k} \dot{u} \\ \end{aligned} \]
\(k u\) が \(k \ddot{u}\) になっているのは式からコードに翻訳したときの打ち間違いなのですが、上手く動いてしまいました。この時点で \(k\) はばね係数ではなくなっています。
\(V[n]\) は入力信号から計算した速度です。
\[ V[n] = x[n] - x[n-1] \]
係数 \(c\) 、 \(k\) 、 \(\alpha\) の範囲は全て 0 以上、 1 以下です。
\[ 0 \leq c \leq 1, \quad 0 \leq k \leq 1, \quad 0 \leq \alpha \leq 1 \]
実装です。
import numpy as np
import scipy.signal as signal
import matplotlib.pyplot as pyplot
class Model:
def __init__(self, damping, spring_k):
self.c = damping
self.k = spring_k
self.acc = 0
self.vel = 0
self.pos = 0
self.x1 = 0
def process(self, x0):
self.acc = self.c * self.vel + self.k * self.acc
self.vel -= self.acc + x0 - self.x1
self.pos -= self.c / (1 - self.k) * self.vel
self.x1 = x0
return self.pos
model = Model(0.01, 0.96)
samplerate = 48000
duration = 0.1
frequency = 60
phase = np.linspace(0, 2 * np.pi * frequency * duration, int(duration * samplerate))
sig = signal.square(phase)
# sig = np.sin(phase)
filtered = np.array([model.process(x) for x in sig])
pyplot.plot(sig)
pyplot.plot(filtered)
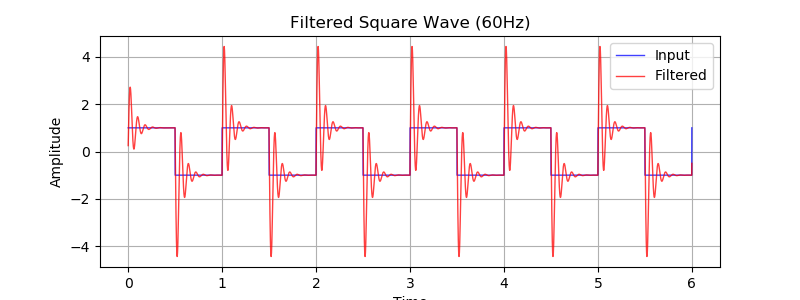
pyplot.show()係数を \(c = 0.01,\ k = 0.96\) として、周波数 60 Hz 、デューティ比 50% の矩形波を入力したときの出力です。

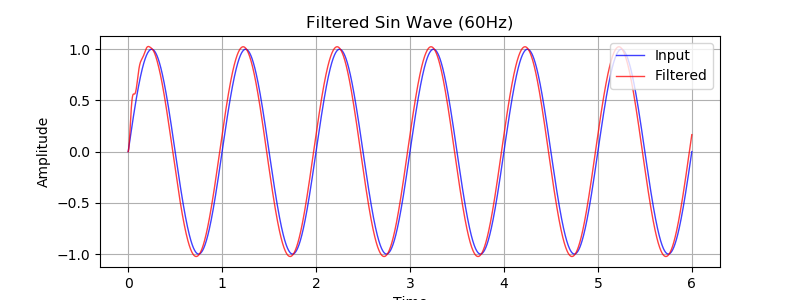
係数を \(c = 0.01,\ k = 0.96\) として 60 Hz のサイン波を入力したときの出力です。
性質を調べて \(c\) と \(k\) をチューニングします。
\(u\) の式で出力の大きさを調整しています。
\[ u \mathrel{{-}{=}} \frac{c}{1 - k} \dot{u} \]
\(\dot{u}\) の係数に \(\dfrac{c}{1 - k}\) を使うとカットオフ周波数が低くなっても出力の大きさがあまり変わりません。
\(\dot{u}\) の係数に \(c\) を使うとカットオフ周波数が低くなると出力も小さくなります。
これらの係数は試行錯誤で見つけました。
フィルタの式に時間のインデックスをつけます。
\[ \begin{aligned} \ddot{u}[n] =& c \dot{u}[n-1] + k \ddot{u}[n-1] \\ \dot{u}[n] =& \dot{u}[n-1] - \ddot{u}[n] - x[n] + x[n-1] \\ u[n] =& \alpha \left( u[n-1] - \frac{c}{1 - k} \dot{u}[n] \right) \\ \end{aligned} \]
\(n\) はサンプル数で表された現在の時刻、 \(\alpha\) は直流を除去するために追加した適当な係数です。
\(u[n]\) の式を \(\dot{u}[n]\) について解きます。
\[ \dot{u}[n] = \frac{1 - k}{c} \left( u[n-1] - \frac{1}{\alpha} u[n] \right) \]
\(\dot{u}[n]\) の式を \(\ddot{u}[n]\) について解きます。
\[ \ddot{u}[n] = \dot{u}[n-1] - \dot{u}[n] - x[n] + x[n-1] \]
Maxima を使って \(u[n-i]\) の項だけが残るように式を変形します。
d1_u(n) := (1 - k) / c * (u(n - 1) - u(n) / α);
d2_u(n) := d1_u(n - 1) - d1_u(n) - x(n) + x(n - 1);
result: d2_u(n) = c * d1_u(n - 1) + k * d2_u(n - 1);
ratvars(u(n), u(n-1), u(n-2), u(n-3), x(n), x(n-1), x(n-2), x(n-3));
ratexpand(0 = lhs(result) - rhs(result));出力です。
\[ \begin{aligned} 0=& - x(n) \\& + k x(n-1) + x( n-1) \\& - k x(n-2) \\& -\frac{k u(n)}{c \alpha}+\frac{u(n)}{c \alpha } \\& +\frac{k^2 u(n-1)}{c \alpha} - \frac{u(n-1)}{c \alpha} - \frac{k u(n-1)}{\alpha} + \frac{u(n-1)}{\alpha} + \frac{k u(n-1)}{c} - \frac{u(n-1)}{c} \\& - \frac{k^2 u(n-2)}{c \alpha} + \frac{k u(n-2)}{c \alpha} - \frac{k^2 u(n-2)}{c} + \frac{u(n-2)}{c} + k u(n-2) - u(n-2) \\& + \frac{k^2 u(n-3)}{c} - \frac{k u(n-3)}{c} \end{aligned} \]
出力を整理した式です。
\[ \begin{aligned} x[n] - (1 + k) x[n-1] + k x[n-2] =& - \frac{k - 1}{c \alpha} u[n] \\& + \left( \frac{k^2 - 1}{c \alpha} - \frac{k - 1}{\alpha} + \frac{k - 1}{c} \right) u[n-1] \\& + \left( -\frac{k^2 - k}{c \alpha} - \frac{k^2 - 1}{c} + k - 1 \right) u[n-2] \\& + \frac{k^2 - k}{c} u[n-3] \end{aligned} \]
伝達関数が得られました。
\[ H(z) = \frac{ 1 - (k + 1) z^{-1} + k z^{-2} }{ C_0 + C_1 z^{-1} + C_2 z^{-2} + C_3 z^{-3} } \qquad \begin{aligned} C_0 &= - \frac{k - 1}{c \alpha} \\ C_1 &= \frac{k^2 - 1}{c \alpha} - \frac{k - 1}{\alpha} + \frac{k - 1}{c} \\ C_2 &= -\frac{k^2 - k}{c \alpha} - \frac{k^2 - 1}{c} + k - 1 \\ C_3 &= \frac{k^2 - k}{c} \\ \end{aligned} \]
Maxima の solve
を試したところ伝達関数からカットオフ周波数 \(\omega_c\)
を計算する式は得られませんでした。そこで scipy.signal.freqz
から得られる振幅特性を基にして \(\omega_c\) から係数 \(c\)
を求める近似曲線を作ることにしました。
係数 \(c\) の値を変えるとカットオフ周波数 \(\omega_c\) が変わるようなので \(c\) と \(\omega_c\) の関係をプロットします。 \(k\) の値は 0 に固定します。
次のコードを Python3 のインタープリタにコピペすると動きます。 NumPy 、 SciPy 、 Matplotlib が必要です。
import numpy as np
import scipy.signal as signal
import matplotlib.pyplot as pyplot
def transferFunction(c, k, α=1):
return (
[1, -(k + 1), k, 0],
[
-(k - 1) / (c * α),
(k * k - 1) / (c * α) - (k - 1) / α + (k - 1) / c,
k * (k - 1) / (c * α) - (k * k - 1) / c + k - 1,
k * (k - 1) / c,
],
)
def cutoffPlot():
cmap = pyplot.get_cmap("viridis")
nPlot = 12
for idx, c in enumerate(np.geomspace(1e-5, 1, nPlot)):
#
# 振幅特性をプロット。
b, a = transferFunction(c, 0.0)
ω, h = signal.freqz(b, a, 2**16)
gain = 20 * np.log10(abs(h))
pyplot.plot(ω, gain, color=cmap(idx / nPlot), label=f"c={c:.3f}")
#
# -3 dB の ω_c を探す。
index = np.argmax(gain <= -3)
if index < 2:
continue
prev = index - 1
delta_range = gain[index] - gain[prev]
ratio = (-3 - gain[prev]) / delta_range
x = ω[prev] + ratio * (ω[index] - ω[prev])
y = gain[prev] + ratio * delta_range
pyplot.scatter(x, y, color=cmap(idx / nPlot))
pyplot.xscale("log")
pyplot.show()
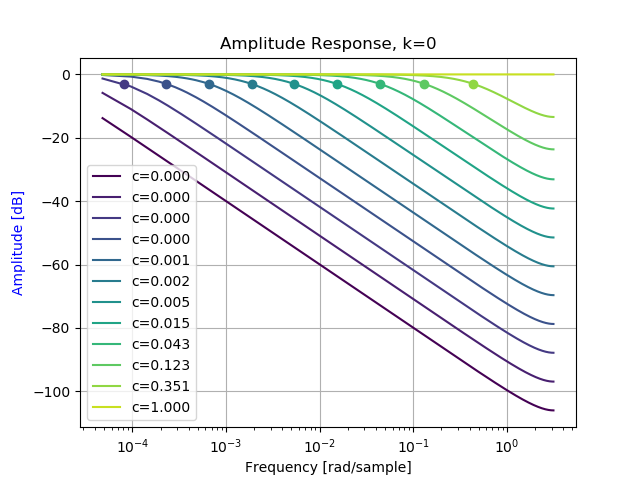
cutoffPlot()出力された振幅特性のプロットです。丸い点は対応する色の振幅特性の -3 dB の位置を表しています。
カットオフ周波数 \(\omega_c\) と対応する係数 \(c\) の値をプロットします。
def dampingCutoffPlot():
cmapReal = pyplot.get_cmap("viridis")
xC = np.linspace(1e-5, 1, 128)
data = []
for idx, c in enumerate(xC):
b, a = transferFunction(c, 0.0)
ω, h = signal.freqz(b, a, 2**16)
gain = 20 * np.log10(abs(h))
index = np.argmax(gain <= -3)
if index < 2:
continue
prev = index - 1
delta_range = gain[index] - gain[prev]
ratio = (-3 - gain[prev]) / delta_range
cutoff = ω[prev] + ratio * (ω[index] - ω[prev])
data.append((c, cutoff))
pyplot.scatter(cutoff, c, color=cmapReal(idx / len(xC)))
#
# [0, 1] に正規化された周波数から c を計算するための近似曲線を求める。
xC_fit, ω_c_fit = zip(*data)
ω_c_fit = np.array(ω_c_fit) / 2 / np.pi
polyCoef = np.polyfit(ω_c_fit, xC_fit, 6)
print([p for p in polyCoef])
polyCoef[-1] = 0 # ω_c = 0 のとき c = 0 となるように定数を変更。
poly = np.poly1d(polyCoef)
curveX = np.linspace(0, 0.5, 1024)
curveY = poly(curveX)
pyplot.plot(curveX * 2 * np.pi, curveY, label="polyfit")
#
# プロット。
pyplot.title("c - ω_c Plot")
pyplot.ylabel("c")
pyplot.xlabel("Cutoff Frequency [rad/sample]")
pyplot.legend()
pyplot.grid()
pyplot.show()
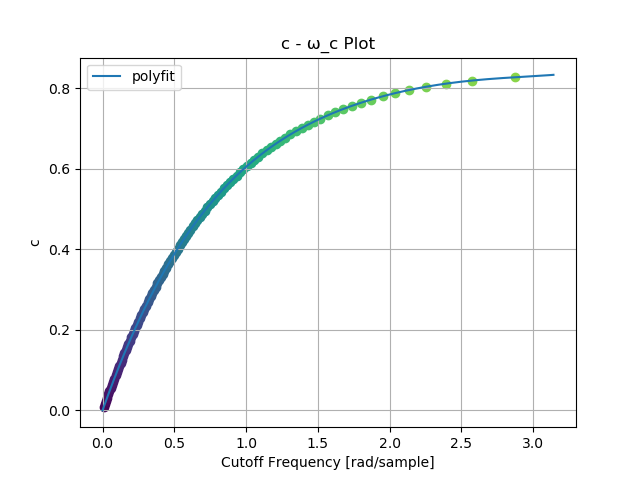
dampingCutoffPlot()出力された \(c \text{--} \omega_c\) プロットです。丸い点が実データ、曲線は 6 次の多項式による近似曲線です。
カットオフ周波数 \(\omega_c\) から係数 \(c\) を求める近似曲線の多項式です。中点 \(\cdot\) は乗算を表しています。 \(x = \dfrac{\omega_c}{\pi}\) と定義しています。
\[ \begin{aligned} c \approx & 56.85341479156533 \cdot x^6 - 60.92051508862034 \cdot x^5 - 1.6515635438744682 \cdot x^4 \\ & + 31.558896956675998 \cdot x^3 - 20.61402812645397 \cdot x^2 + 6.320753515093109 \cdot x \end{aligned} \]
カットオフ周波数 \(\omega_c\) から係数 \(c\) を求める多項式の C++ の実装です。
float lowpassHzToC(float sampleRate, float cutoffHz)
{
float x = cutoffHz / sampleRate;
return float(56.85341479156533) * x * x * x * x * x * x
+ float(-60.92051508862034) * x * x * x * x * x
+ float(-1.6515635438744682) * x * x * x * x
+ float(31.558896956675998) * x * x * x
+ float(-20.61402812645397) * x * x
+ float(6.320753515093109) * x;
}次のような式の書き方もできますが、 g++ -O3 で chrono
を使って簡単なベンチマークを取ったところ、私の環境では計算速度は変わらなかったです。
float lowpassHzToC(float sampleRate, float cutoffHz)
{
float x = cutoffHz / sampleRate;
return (((((float(56.85341479156533) * x + float(-60.92051508862034)
) * x + float(-1.6515635438744682)
) * x + float(31.558896956675998)
) * x + float(-20.61402812645397)
) * x + float(6.320753515093109)
) * x;
}フィルタの式の係数 \(k\) を変えるとレゾナンスが変わるようです。レゾナンスを変えたときの振幅のピークが一定になるようにチューニングします。
まずは \(k\) を変えたときに振幅特性のピークがどう変わるかを調べました。
def resonancePeakPlot():
cmap = pyplot.get_cmap("viridis")
nC = 10
kArray = 1 - np.geomspace(1e-5, 1, 128)
for idx, c in enumerate(np.linspace(0.1, 1, nC)):
dataY = []
for k in kArray:
b, a = transferFunction(c, k, 1)
ω, h = signal.freqz(b, a, 2**16)
h[np.isfinite(h) == False] = 0
peak = np.max(np.abs(h))
if not np.isfinite(peak):
print(idx, c, k, peak)
dataY.append(peak)
pyplot.plot(1 - kArray, dataY, color=cmap(idx / nC), label=f"c={c:.3f}")
pyplot.ylabel("Peak Amplitude")
pyplot.xlabel("1 - k")
pyplot.xscale("log")
pyplot.yscale("log")
pyplot.grid()
pyplot.legend()
pyplot.show()
resonancePeakPlot()出力されたプロットです。
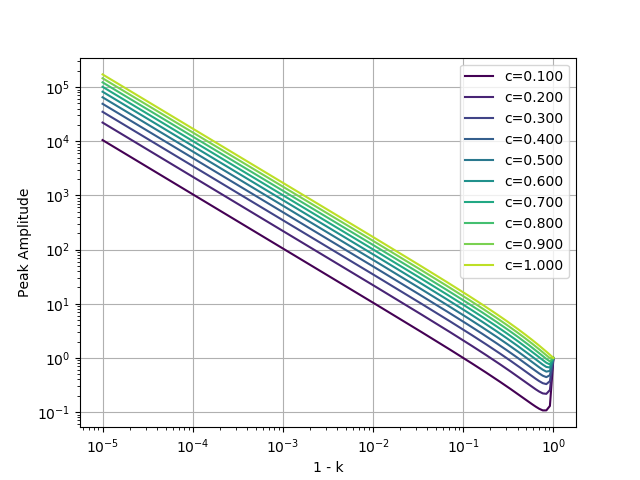
\(c\) の値によらず、 \(1 - k\) が 0 に近づくと指数関数的にピークが大きくなっています。近似曲線を 1 つ作って \(c\) に応じてスケーリングを変えれば良さそうです。
振幅特性のピークの値と係数 \(c\)
の値を決めたときの \(k\)
を二分探索で探します。次のコードを実行すると data.json
ファイルを作成して計算結果を書き込みます。
import json
def findUniformResonance():
maxIteration = 256
data = []
targetPeak = np.geomspace(1, 1e5, 16)
nC = 128
xC = np.geomspace(1e-4, 1, nC)
for target in targetPeak:
peakData = []
for c in xC:
jdx = 0
diff = 1
k = 0.5
delta = k
peak = 0
while diff > 1e-5 and jdx < maxIteration:
b, a = transferFunction(c, k)
ω, h = signal.freqz(b, a, 2**16)
h[np.isfinite(h) == False] = 0
peak = np.max(np.abs(h))
diff = abs(target - peak)
delta *= 0.5
if peak < target:
k += delta
else:
k -= delta
jdx += 1
print(f"{target}, {c}, {k}, {peak}")
peakData.append({"c": c, "k": k, "peak": peak})
data.append({
"targetPeak": target,
"c": [d["c"] for d in peakData],
"k": [d["k"] for d in peakData],
"peak": [d["peak"] for d in peakData],
})
with open("data.json", "w") as fi:
json.dump(data, fi, indent=2)
findUniformResonance()出力された data.json から \(c\) と \(k\)
についてプロットします。点線は近似曲線です。
def plotResonance(data):
cmapV = pyplot.get_cmap("viridis")
cmapP = pyplot.get_cmap("plasma")
for idx, dat in enumerate(data):
if dat["targetPeak"] == 1.0:
continue
damping = np.array(dat["c"])
spring = np.array(dat["k"])
peak = np.array(dat["peak"])
pyplot.plot(
damping,
1 - spring,
lw=1,
color=cmapV(idx / len(data)),
label=f"Peak={dat['targetPeak']:g}")
kMin = np.min(spring)
kMax = np.max(spring)
y = kMax - (kMax - kMin) * np.arccos(1 - np.array(damping)) / (np.pi / 2)
pyplot.plot(damping, 1 - y, lw=1, ls=":", color=cmapP(idx / len(data)))
pyplot.title("c-k Plot (dotted line is approximation)")
pyplot.xlabel("c")
pyplot.ylabel("1 - k")
pyplot.yscale("log")
pyplot.legend(ncol=2)
pyplot.grid()
pyplot.tight_layout()
pyplot.show()
with open("data.json", "r") as fi:
data = json.load(fi)
plotResonance(data)出力されたプロットです。実線は data.json
からプロットした実データ、点線は近似曲線です。
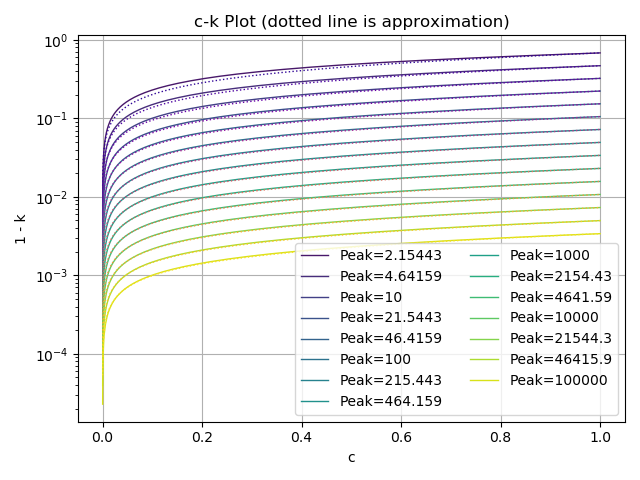
近似曲線の式です。
\[ k \approx k_{\mathrm{Max}} - \frac{2}{\pi} (k_{\mathrm{Max}} - k_{\mathrm{Min}}) \arccos(1 - c) \]
近似曲線は \(\arccos\) を使って試行錯誤で作りました。 \(\arccos\) の利用は \(1-k\) の軸を線形スケールにしたときのプロットを見て適当に決めました。
\(\arccos\) による近似曲線はピークが小さくなるほど実際の特性からずれていますが、ピークが大きいときはよく近似できているように見えます。
上の \(c \text{--} k\) プロットでは \(k_{\mathrm{Min}}\) と \(k_{\mathrm{Max}}\) を実データから取得して近似曲線を計算しています。 DSP の計算中には実データは使えないので \(k_{\mathrm{Min}}\) と \(k_{\mathrm{Max}}\) の近似曲線を作ります。
def plotSpringMinMax(data):
kMin = []
kMax = []
target = []
for idx, dat in enumerate(data):
damping = dat["c"]
spring = dat["k"]
peak = dat["peak"]
target.append(dat["targetPeak"])
kMin.append(np.min(spring))
kMax.append(np.max(spring))
#
# kMin plot.
resonance = np.linspace(0, 1, 1024)
alpha = np.log(1 - kMin[-1])
y = 1 - np.exp(alpha * resonance)
print(alpha)
pyplot.plot(
resonance, y, zorder=3, alpha=0.75, color="#00ff00", label="approx.")
fitX = np.linspace(0, 1, len(kMin))
pyplot.plot(fitX, kMin, lw=4, zorder=2, color="black", label="kMin")
pyplot.title("k_Min-Resonance Plot")
pyplot.xlabel("Resonance")
pyplot.ylabel("k")
pyplot.grid()
pyplot.legend()
pyplot.show()
#
# KMax plot.
resonance = np.linspace(0, 1, 1024)
offset = 1 - kMin[-1]
alpha = np.log(offset)
y = kMax[-1] - 0.01 * (np.exp(alpha * resonance) - offset)
pyplot.plot(
resonance, y, zorder=3, alpha=0.75, color="#00ff00", label="approx.")
print(kMax[-1], alpha, offset)
pyplot.plot(fitX, kMax, lw=4, zorder=2, color="black", label="kMax")
pyplot.title("k_Max-Resonance Plot")
pyplot.xlabel("Resonance")
pyplot.ylabel("k")
pyplot.grid(zorder=1)
pyplot.legend()
pyplot.tight_layout()
pyplot.show()
plotSpringMinMax(data)出力されたプロットです。黒い線が実データ、緑の線
approx. は近似曲線です。
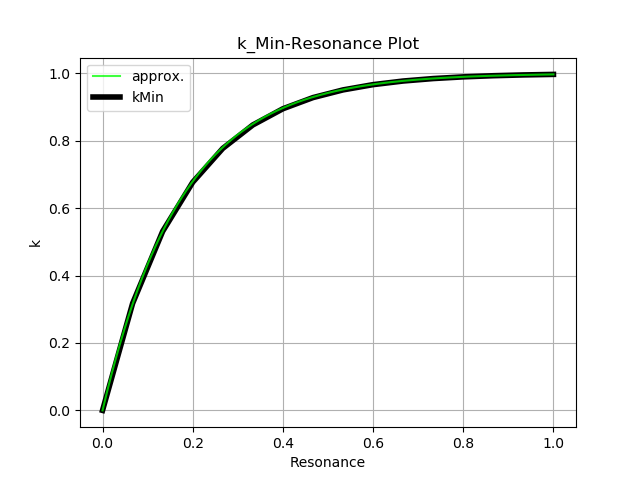
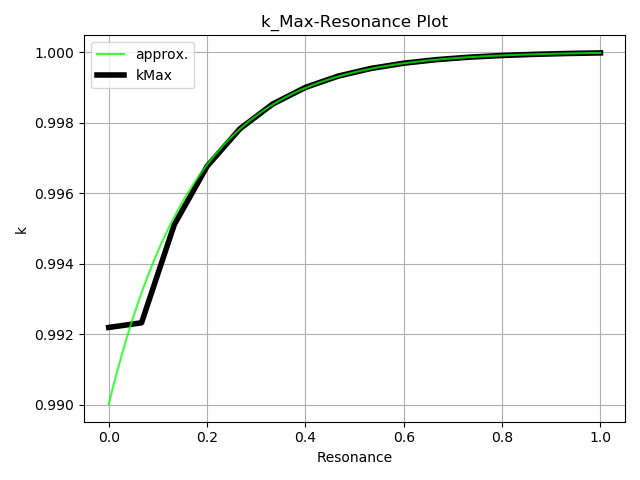
\(k_{\mathrm{Min}}\) の近似曲線の式です。 \(\mathtt{resonance}\) はユーザが指定するレゾナンスの値で、範囲は \([0, 1]\) です。
\[ k_{\mathrm{Min}} = 1 - \exp(-5.6852537097945195 \cdot \mathtt{resonance}) \]
\(k_{\mathrm{Max}}\) の近似曲線の式です。
\[ \begin{aligned} k_{\mathrm{Max}} =& 0.9999771732485103 \\ &- 0.01 \cdot (\exp(-5.6852537097945195 \cdot \mathtt{resonance}) - 0.0033956716251850594) \end{aligned} \]
レゾナンスのチューニングができました。 C++ で実装します。
#include <algorithm>
#include <cmath>
constexpr double halfpi = 1.57079632679489661923;
float resonanceToK(float c, float resonance, bool uniformPeak)
{
float kExp = expf(float(-5.6852537097945195) * resonance);
float kMin = float(1) - kExp;
float kMax = float(0.9999771732485103)
- float(0.01) * (kExp - float(0.0033956716251850594));
return kMax - (kMax - kMin) * acosf(float(1) - c) / float(halfpi);
}カットオフ周波数とレゾナンスのチューニングを終えて、プラグインにして試していると直流が乗ることに気がついたので \(\alpha\) を追加しました。 \(\alpha\) を変えるとハイパスフィルタのカットオフ周波数が変わるようです。
ローパスのカットオフ周波数とチューニングの手順は同じなので結果だけ掲載します。
カットオフ周波数 \(\omega_c\)
に対応する \(\alpha\)
の値のプロットです。丸い点が実データ、 曲線は指数関数を使って scipy.optimize.curve_fit
で求めた近似です。
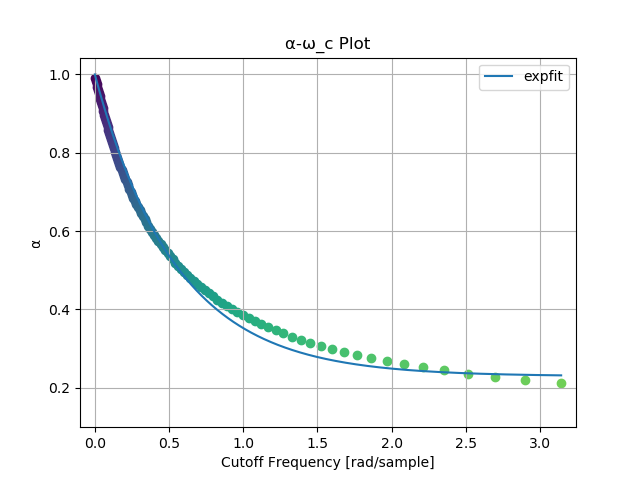
expfit の式です。
\[ \alpha = 0.5638865655409118 + 0.43611343445908823 \cdot \exp(-6.501239408777854 x) \]
カットオフを -3 dB から -6 dB に変えたときの式も求めました。こちらのほうが \(\alpha\) の範囲を広く使えます。
\[ \alpha = 0.39299084333814804 + 0.607009156661852 \cdot \exp(-4.939791161282682 x) \]
C++ による実装例です。
#include <algorithm>
#include <cmath>
template<typename Sample> class LP3 {
public:
void reset() { acc = vel = pos = x1 = 0; }
void set(
Sample sampleRate,
Sample lowpassHz,
Sample highpassHz,
Sample resonance,
bool uniformPeak,
bool uniformGain)
{
Sample x = lowpassHz / sampleRate;
c = Sample(56.85341479156533) * x * x * x * x * x * x
+ Sample(-60.92051508862034) * x * x * x * x * x
+ Sample(-1.6515635438744682) * x * x * x * x
+ Sample(31.558896956675998) * x * x * x
+ Sample(-20.61402812645397) * x * x
+ Sample(6.320753515093109) * x;
if (uniformPeak) {
Sample kExp = exp(Sample(-5.6852537097945195) * resonance);
Sample kMin = Sample(1) - kExp;
Sample kMax = Sample(0.9999771732485103)
- Sample(0.01) * (kExp - Sample(0.0033956716251850594));
k = kMax - (kMax - kMin) * acos(Sample(1) - c) / Sample(halfpi);
} else {
k = std::clamp<Sample>(resonance, Sample(0), Sample(1 - 1e-5));
}
alpha = Sample(0.5638865655409118)
+ Sample(0.43611343445908823) * exp(Sample(-6.501239408777854) * x);
this->uniformGain = uniformGain;
}
Sample process(Sample x0)
{
acc = k * acc + c * vel;
vel -= acc + x0 - x1;
pos -= (uniformGain ? c / (1 - k) : c) * vel;
pos *= Sample(alpha);
x1 = x0;
return pos;
}
private:
Sample c = 0;
Sample k = 0;
Sample alpha = 1;
bool uniformGain = true;
Sample acc = 0;
Sample vel = 0;
Sample pos = 0;
Sample x1 = 0;
};LV2 プラグインとして実装したフィルタのコードへのリンクです。
フィルタの音のサンプルです。
scipy.signal.sawtooth で生成した 45 Hz
の鋸歯波。uniformGain は False 。サンプルの生成に使ったコードへのリンクです。実行には NumPy 、 SciPy 、 Matplotlib 、 Soundfile が必要です。
\(\arccos\) を使った近似曲線は \(\dfrac{b_0 + b_1 x + b_2 x^2 \dots}{a_0 + a_1 x + a_2 x^2 \dots}\) という形の分数でも近似できそうです。
レゾナンスのチューニングは計算が重たいので、効率を重視するなら省略できます。
ポリフォニックシンセでノートオンごとにフィルタの状態をリセットするとき、ローパスしか使わないなら \(\alpha\) を 1 に固定して処理を減らせます。
FL Studio で使える Fast LP と似たような音が出ます。