何かあれば GitHub のリポジトリに issue を作るか ryukau@gmail.com までお気軽にどうぞ。
Update: 2025-01-07
ウェーブテーブルの帯域制限と位相方向の補間について調べます。
コードは Python3 です。上から順にインタプリタにコピペしていけばコードが実行できるようになっています。実行には NumPy, SciPy, matplotlib が必要です。
より完全なウェーブテーブルの実装をウェーブテーブルのピッチベンドに掲載しています。
import numpy
def saw_spectrum(size):
spec = [0] + [(-1)**k / k for k in range(1, int(size / 2 + 1))]
spec = -1j * size / numpy.pi * numpy.array(spec)
return spec
def naive_saw(samplerate, phase, size=512):
spec = saw_spectrum(size)
table = numpy.fft.irfft(spec)
xp = numpy.linspace(0, 1, len(table))
return numpy.interp(phase % 1.0, xp, table)
def dry_phase(samplerate, duration, base_freq):
time = numpy.linspace(0, duration, int(samplerate * duration))
return base_freq * time
samplerate = 44100
duration = 1
base_freq = 1000
table_size = 1024
phase = dry_phase(samplerate, duration, base_freq)
naive = naive_saw(samplerate, phase, table_size)saw_spectrum
はのこぎり波のスペクトラムを計算しています。のこぎり波は次のフーリエ級数で表されます。
\[ b_n = -\frac{(-1)^n A}{n \pi} \]
\(b_n\)
はフーリエ級数のサイン波の係数です。 \(n\) は倍音の次数、 \(A\) は音量です。実装では \(A\) が size
になっています。
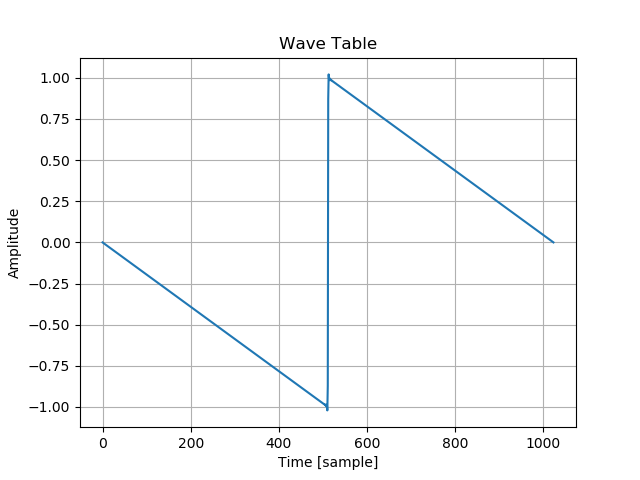
のこぎり波のスペクトラムを irfft
でウェーブテーブルに変換しています。 table
には次のような波形が格納されています。

加算合成したのこぎり波と比較します。
import matplotlib.pyplot as pyplot
def to_decibel(data):
data_abs = numpy.abs(data)
return 20 * numpy.log10(data_abs / numpy.max(data_abs))
def compare(true_sig, real_sig):
true_spec = to_decibel(numpy.abs(numpy.fft.rfft(true_sig)))
real_spec = to_decibel(numpy.abs(numpy.fft.rfft(real_sig)))
pyplot.plot(true_spec, label="True", alpha=0.75, lw=2, color="blue")
pyplot.plot(real_spec, label="Real", alpha=0.75, lw=1, color="red")
pyplot.grid()
pyplot.legend()
pyplot.ylim((-200, 10))
pyplot.show()
def additive_saw(samplerate, base_freq, phase):
omega_t = 2 * numpy.pi * phase
sig = numpy.zeros_like(omega_t)
overtone = numpy.arange(base_freq, samplerate / 2, base_freq)
for k, freq in enumerate(overtone, 1):
sig += ((-1)**k / k) * numpy.sin(k * omega_t)
return 2 * sig / numpy.pi
additive = additive_saw(samplerate, base_freq, phase)
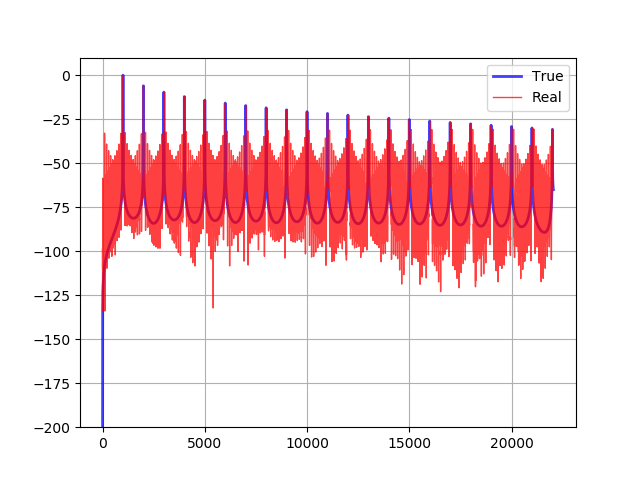
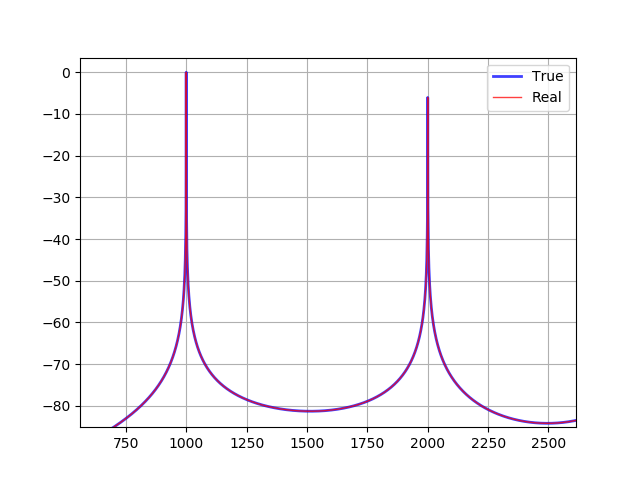
compare(additive, naive)コードの実行結果です。図の縦軸は dB で表した周波数成分の大きさ、横軸は周波数です。青が加算合成した1000Hzののこぎり波のスペクトラム、赤が素朴なウェーブテーブルで合成したのこぎり波のスペクトラムです。
1つめの倍音と2つめの倍音の間を拡大した図です。
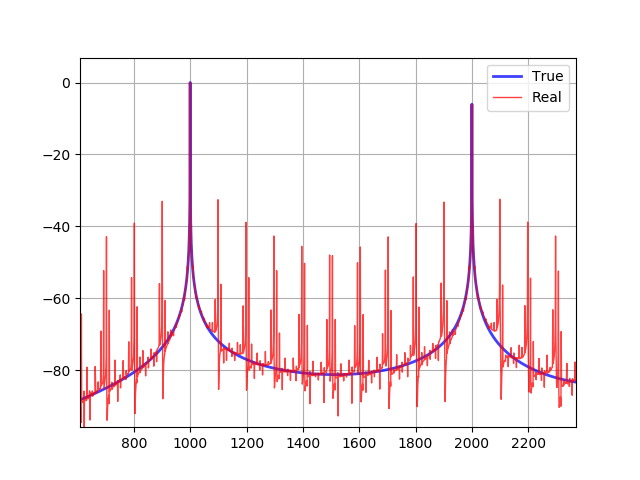
赤と青の線が一致していない分だけノイズがのっています。
Yoshimi の ADDsynth で使われているテクニックでノイズを大幅に低減できます。Yoshimi の ADDsynth はウェーブテーブルのデータをスペクトラムとして持っています。ノートオンのたびに保持しているスペクトラムからナイキスト周波数を超える倍音を取り除いた上で IFFT してウェーブテーブルを作成しています。
サンプリング周波数を \(f_s\) 、合成する音の周波数を \(f\) とするとナイキスト周波数を超えない最大の倍音の次数は \(N_{h} = \left\lfloor \dfrac{f_s}{2f} \right\rfloor\) となります。よって IFFT する直前に \(N_h + 1\) より高い周波数成分の値を 0 にすることでエイリアシングを大幅に低減することができます。
def yoshimi_saw_linterp(samplerate, base_freq, phase, size=512):
spec = saw_spectrum(size)
n_harmonics = int(samplerate / 2 / base_freq)
spec[n_harmonics + 1:] = 0
table = numpy.fft.irfft(spec)
xp = numpy.linspace(0, 1, len(table))
return numpy.interp(phase % 1.0, xp, table)
linterp = yoshimi_saw_linterp(samplerate, base_freq, phase)
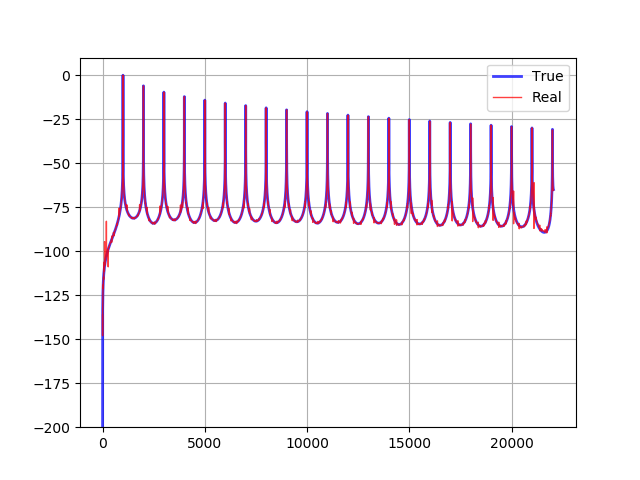
compare(additive, linterp)実行結果です。青が加算合成のスペクトラム、赤が Yoshimi のテクニックを使ったウェーブテーブルのスペクトラムです。
1つめの倍音と2つめの倍音の間を拡大した図です。
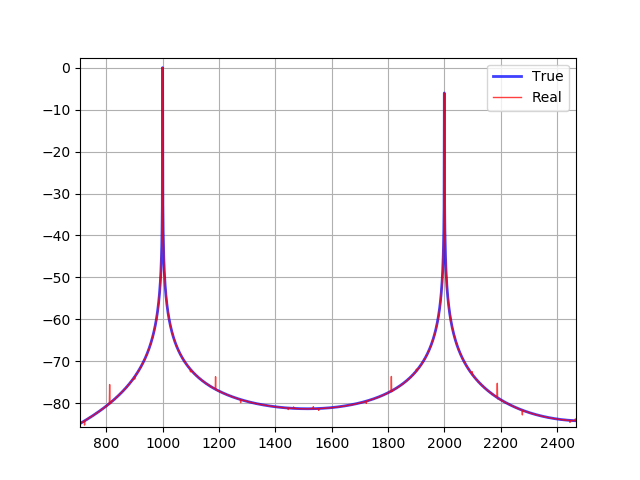
大幅にノイズが減りました。
ここまでは線形補間を使っていましたが、キュービック補間や sinc 補間を使うことでさらにノイズを低減できます。
キュービック補間を使ったウェーブテーブルの実装です。キュービック補間の計算に
scipy.interpolate.CubicSpline
を使っています。
import scipy.interpolate as interpolate
def yoshimi_saw_cubic(samplerate, base_freq, phase, size=512):
spec = saw_spectrum(size)
n_harmonics = int(samplerate / 2 / base_freq)
spec[n_harmonics + 1:] = 0
table = numpy.fft.irfft(spec)
table = numpy.append(table, [table[0]])
xp = numpy.linspace(0, 1, len(table))
interp = interpolate.CubicSpline(xp, table, bc_type="periodic")
return interp(phase % 1.0)
cubic = yoshimi_saw_cubic(samplerate, base_freq, phase)
compare(additive, cubic)実行結果です。赤がキュービック補間を使った Yoshimi のウェーブテーブルのスペクトラムです。
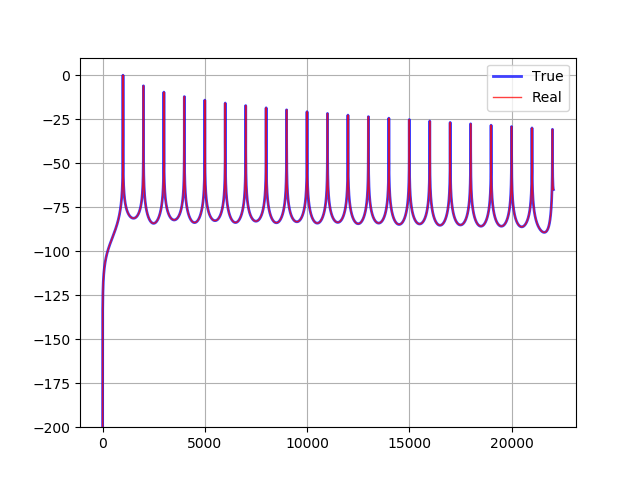
1つめの倍音と2つめの倍音の間を拡大した図です。
Sinc 補間は次の式で計算できます。
\[ \begin{aligned} x(j) &= \sum_{i=0}^{N-1} x[i]\,\mathrm{sinc}(j - i)\\ \mathrm{sinc}(i) &= \begin{cases} \dfrac{\sin(\pi i)}{\pi i}, & \mathrm{if}\ i \neq 0,\\ 1, & \mathrm{if}\ i = 0. \end{cases} \end{aligned} \]
Sinc 補間を使ったウェーブテーブルの実装です。 Sinc 関数の計算に numpy.sinc
を使っています。
import scipy.signal as signal
def sinc_saw(samplerate, base_freq, phase, size=512):
spec = saw_spectrum(size)
n_harmonics = int(samplerate / 2 / base_freq)
spec[n_harmonics + 1:] = 0
table = numpy.fft.irfft(spec) # ウェーブテーブル
window = signal.windows.kaiser(len(table) - 1, 2.0952)
window = numpy.insert(window, 0, 0) # 奇数次の窓関数。
half = len(window) // 2
w_index = numpy.arange(-half, half) # Sinc 補間の式の i 。
phase = phase % 1.0 * len(table)
sig = numpy.zeros_like(phase)
for sig_index, ph in enumerate(phase):
win = window * numpy.sinc(ph % 1.0 - w_index) # Sinc 補間の係数。
rolled = numpy.roll(table, half - int(ph))[:len(window)]
sig[sig_index] = numpy.sum(win * rolled)
return sig
sinc = sinc_saw(samplerate, base_freq, phase)
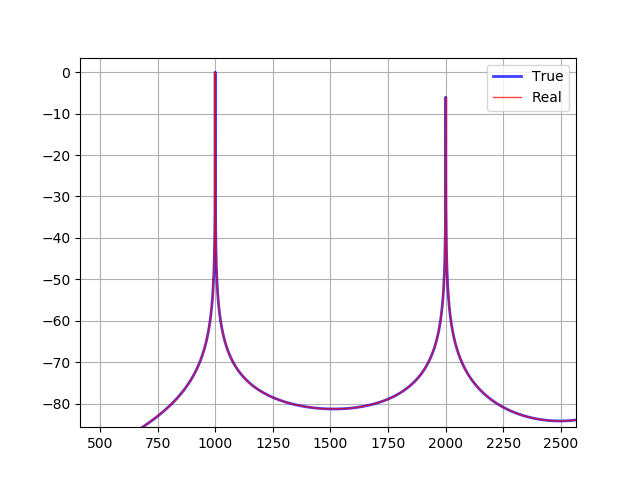
compare(additive, sinc)実行結果です。赤がキュービック補間を使った Yoshimi のウェーブテーブルのスペクトラムです。
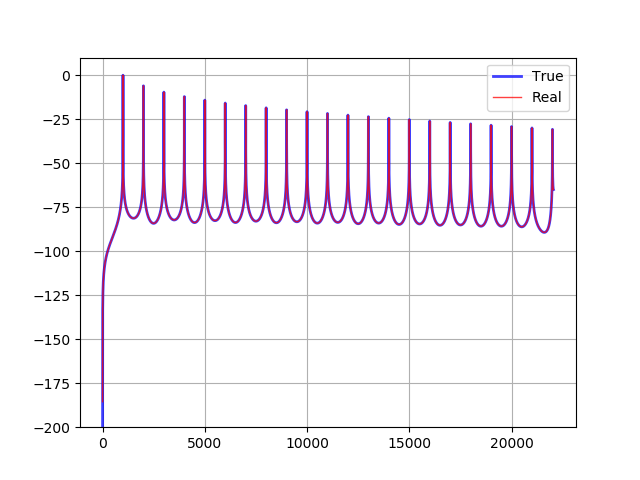
1つめの倍音と2つめの倍音の間を拡大した図です。
見た目ではノイズがわからないようになりました。以降では加算合成した信号のスペクトラムとウェーブテーブルで合成した信号の平均絶対誤差を使って評価します。
2つの信号のスペクトラムの平均絶対誤差を計算する関数です。
import pprint
def mean_absolute_error(true_sig, real_sig):
true_spec = to_decibel(numpy.abs(numpy.fft.rfft(true_sig)))
real_spec = to_decibel(numpy.abs(numpy.fft.rfft(real_sig)))
return numpy.nanmean(numpy.abs(true_spec - real_spec))
def calc_error(additive, naive, linterp, cubic, sinc):
return {
"naive": mean_absolute_error(additive, naive),
"linterp": mean_absolute_error(additive, linterp),
"cubic": mean_absolute_error(additive, cubic),
"sinc": mean_absolute_error(additive, sinc),
}
errors = calc_error(additive, naive, linterp, cubic, sinc)
pp = pprint.PrettyPrinter(indent=4)
pp.pprint(errors)読みやすさのために整えた実行結果です。
'naive' : 7.914086306044551
'linterp': 0.01530352147107085
'cubic' : 0.0005218573155090014
'sinc' : 0.0032115018908482383キュービック補間の誤差が最も小さくなりました。
変調をかけたときの誤差を調べます。
def generate_wave(samplerate, duration, frequency, type="sin"):
time = numpy.linspace(0, duration, int(samplerate * duration))
phase = 2 * numpy.pi * frequency * time
if type == "saw":
return signal.sawtooth(phase, 1)
if type == "square":
return signal.square(phase, 0.5)
return numpy.sin(phase)
def fm_phase(samplerate, base_freq, mod_amount, mod):
"""freq = base ± lfo_amount."""
freq = base_freq + mod_amount * mod
return (freq / samplerate).cumsum()
lfo_freq = 2
mod_amount = 70
lfo = generate_wave(samplerate, duration, lfo_freq)
phase = fm_phase(samplerate, base_freq, mod_amount, lfo)
additive = additive_saw(samplerate, base_freq, phase)
naive = naive_saw(samplerate, phase, table_size)
linterp = yoshimi_saw_linterp(samplerate, base_freq, phase, table_size)
cubic = yoshimi_saw_cubic(samplerate, base_freq, phase, table_size)
sinc = sinc_saw(samplerate, base_freq, phase, table_size)
errors = calc_error(additive, naive, linterp, cubic, sinc)
pp.pprint(errors)整形した実行結果です。
'naive' : 21.15172242905035
'linterp': 4.534071784520711
'cubic' : 0.02494692724398319
'sinc' : 0.6408277641316118変調をかけたときもキュービック補間の誤差が最も小さくなりました。
Sinc 補間がいまいちだったので試しに base_freq = 100
として誤差を計算したところ次の値が出ました。
'naive' : 3.672971097762815
'linterp': 2.156972873744029
'cubic' : 0.028429699764866655
'sinc' : 0.0009842215677754215Sinc 補間の誤差が最も小さくなっています。
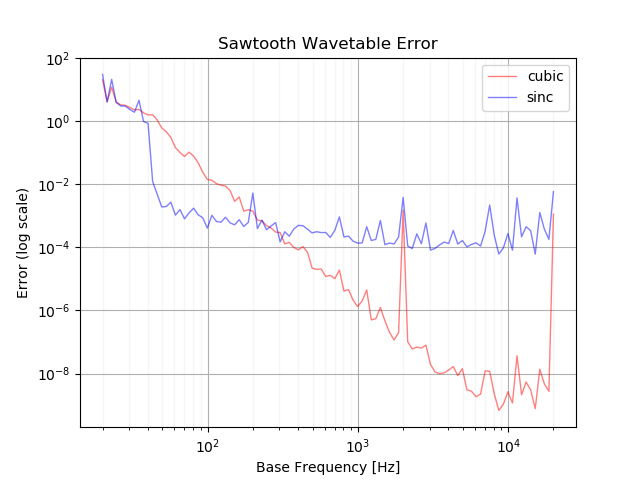
base_freq を変えたときのキュービック補間と sinc
補間の誤差の変化を調べます。次のパラメータを使いました。
samplerate = 44100
duration = 1
base_freq = numpy.geomspace(20, 20000, 100)
table_size = 1024
lfo_freq = 2
mod_amount = 70変調なしのときのウェーブテーブルの誤差です。
変調ありのときのウェーブテーブルの誤差です。
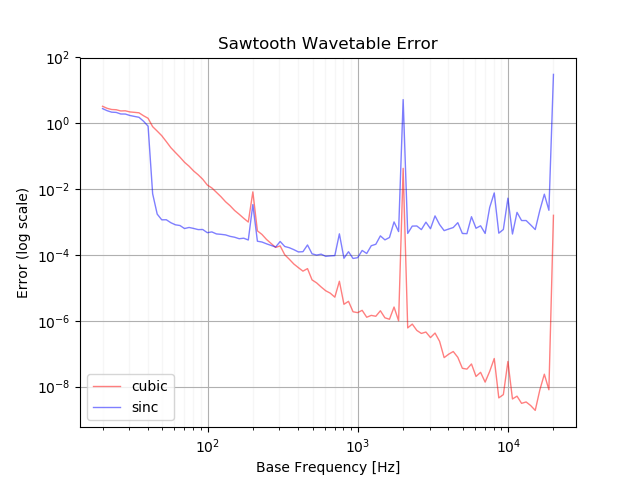
どちらの図も次のように見えます。
耳で聞いても違いが分からないので、計算コストの差を考えるとキュービック補間で十分な気がします。
1000Hz、変調なし。 Naive は耳で聞き取れるノイズがのっています。
1000Hz、変調あり。 Naive は耳で聞き取れるノイズがのっています。
100Hz、変調なし。
100Hz、変調あり。
キュービック補間の補間関数 \(p(t)\) です。ここでは入力されるサンプルが等間隔に並んでいることを仮定しています。 \(t\) の範囲は \([0, 1]\) です。
\[ \begin{aligned} p(t) &= y[i-1] h_{00}(t) + m[i-1] h_{10}(t) + y[i-2] h_{01}(t) + m[i-2] h_{11}(t)\\ h_{00}(t) &= 2 t^3 - 3 t^2 + 1\\ h_{10}(t) &= t^3 - 2 t^2 + t\\ h_{01}(t) &= -2 t^3 + 3 t^2\\ h_{11}(t) &= t^3 - t^2 \end{aligned} \]
\(p(t)\) に \(h_{00}(t)\) から \(h_{11}(t)\) までを代入します。
\[ \begin{aligned} p(t) &= y[i-1] h_{00}(t) + m[i-1] h_{10}(t) + y[i-2] h_{01}(t) + m[i-2] h_{11}(t) \\ &= y[i-1] (2 t^3 - 3 t^2 + 1) + m[i-1] (t^3 - 2 t^2 + t) + y[i-2] (-2 t^3 + 3 t^2) + m[i-2] (t^3 - t^2) \\ &= (2(y[i-1] - y[i-2]) + m[i-1] + m[i-2]) t^3 - (3(y[i-1] - y[i-2]) + 2 m[i-1] + m[i-2]) t^2 + m[i-1] t + y[i-1] \end{aligned} \]
整理します。
\[ \begin{aligned} p(t) &= C_3 t^3 - (C_2 + C_3) t^2 + C_1 t + y[i-1]\\ C_0 &= y[i-1]- y[i-2]\\ C_1 &= m[i-1]\\ C_2 &= C_0 + C_1\\ C_3 &= C_0 + C_2 + m[i-2]\\ \end{aligned} \]
あとはこの式に \(m[i]\) を代入すれば計算できる形になります。 \(m[i]\) の定義はいくつかあるようです。ここでは有限差分 (Finite Difference) による \(m[i]\) を使います。
\[ m[i-1] = \frac{1}{2} \left( \frac{y[i-2] - y[i-1]}{x[i-1] - x[i-2]} + \frac{y[i-1] - y[i]}{x[i] - x[i-1]} \right) = \frac{y[i-2] - y[i]}{2} \]
今回は \(x\) が等間隔にサンプリングされているので \(x[i-1] - x[i-2]\) と \(x[i] - x[i-1]\) を1に置き換えることができます。
実装します。
def cinterp(y0, y1, y2, y3, t):
"""t の範囲は [0, 1] 。 y1 と y2 の間を補間。"""
t2 = t * t
c0 = y1 - y2
c1 = (y2 - y0) / 2
c2 = c0 + c1
c3 = c0 + c2 + (y3 - y1) / 2
return c3 * t * t2 - (c2 + c3) * t2 + c1 * t + y1このキュービック補間は Catmull-Rom 補間と呼ばれます。
C++ などで -mfma や -ffast-math
を使わないのであれば、以下のように Horner’s method
を使うように書き換えたほうがいいかもしれません。
def cinterp(y0, y1, y2, y3, t):
c0 = y1 - y2
c1 = (y2 - y0) * 0.5
c2 = c0 + c1
c3 = c0 + c2 + (y3 - y1) * 0.5
return ((c3 * t - c2 - c3) * t + c1) * t + y1