何かあれば GitHub のリポジトリに issue を作るか ryukau@gmail.com までお気軽にどうぞ。
Update: 2025-01-07
リミッタのエンベロープのスムーシングに使うためにステップ応答が S 字を描くフィルタについて調べました。
次の 3 つのフィルタを比較します。
\(x\) を入力信号、 \(n\) を現在時刻のサンプル数、 \(N\) をフィルタの長さ (タップ数) とすると、移動平均フィルタは次の式で計算できます。
\[ y[n] = \frac{1}{N} \sum_{i=0}^{N-1} x[n - i] \]
移動平均フィルタはフィルタ係数がすべて \(\dfrac{1}{N}\) の矩形窓を畳み込む FIR フィルタと言い換えることができます。
直列につないだ FIR フィルタは、フィルタ係数を畳み込むことで 1 つのフィルタにまとめられます。矩形窓を畳み込んで、重ね掛けしたときのフィルタ係数がどうなるのか見てみます。
# Python3
import matplotlib.pyplot as plt
import numpy as np
import scipy.signal as signal
def average(fir):
denom = np.sum(fir)
if denom == 0:
return fir
return fir / denom
def movingAverage(nTaps, integrate=0):
length = nTaps // 2**integrate
taps1 = average(np.ones(length))
for _ in range(integrate):
taps2 = average(np.ones(length + 1)) # フィルタのタップ数をそろえるために +1 。
taps1 = average(signal.convolve(taps1, taps2))
length *= 2
return taps1
def plotFilter(nPlot=4, nTaps = 512):
cmap = plt.get_cmap("viridis")
for order in range(nPlot):
taps = movingAverage(nTaps, order)
plt.plot(taps, lw=1, color=cmap(order / nPlot), label=f"{order}")
plt.grid()
plt.legend()
plt.show()
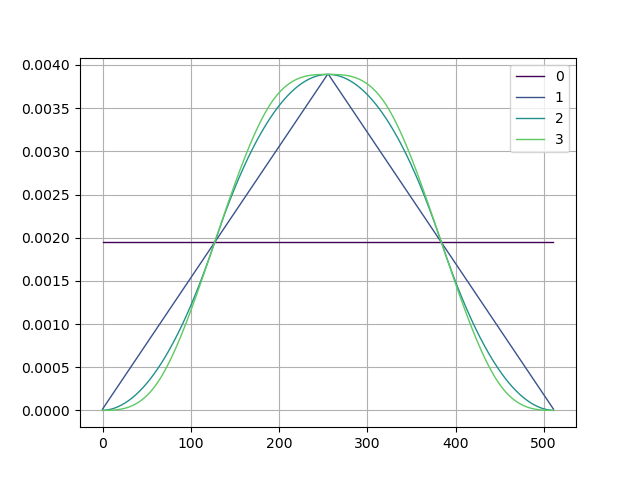
plotFilter()出力です。 1 回畳み込んだときに三角窓になっています。 2 回目以降の畳み込みでは区間ごとに変わる多項式 (piecewise polynomial) になるようです。

移動平均フィルタを畳み込んだフィルタのステップ応答を確認します。
# Python3
def plotStep(nPlot=4, nTaps = 512):
sig = np.hstack((np.zeros(nTaps), np.ones(2 * nTaps)))
cmap = plt.get_cmap("viridis")
for order in range(nPlot):
taps = movingAverage(nTaps, order)
out = signal.lfilter(taps, 1, sig)
plt.plot(out, lw=1, color=cmap(order / nPlot), label=f"{order}")
plt.axvline(2 * nTaps, lw=1, color="black", alpha=0.5, ls="--")
plt.plot(sig, lw=1, color="black", label="Input")
plt.grid()
plt.legend()
plt.show()
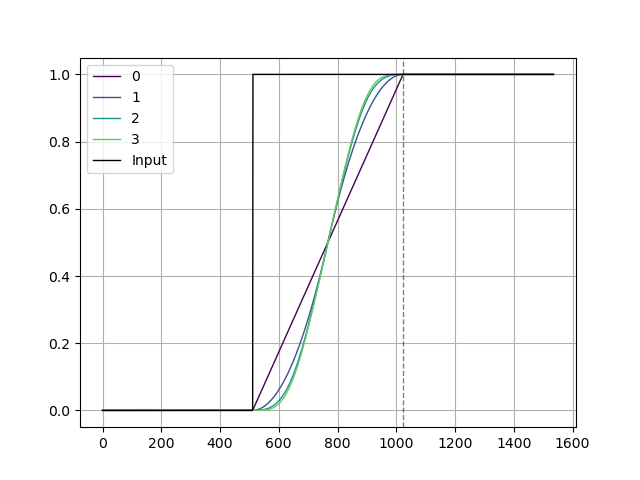
plotStep()出力です。 1 回以上畳み込んだフィルタはステップ応答が S 字になっています。
移動平均フィルタは Musicdsp.org の Lookahead Limiter のページで紹介されている手法を使えば効率よく計算できます。このページでは移動平均の重ね掛けを 1 回行って、フィルタ係数を矩形窓から三角窓の形に変えています。
状態変数 \(s\) を用意します。時点 \(n\) の移動平均フィルタの出力は次の式で計算できます。
\[ s[n] = s[n - 1] + \frac{x[n] - x[n - N]}{N} \]
移動平均フィルタを冒頭で紹介した定義から直接計算するとフィルタのタップ数 \(N\) より 1 サンプルあたりの計算量は \(O(N)\) です。 ディレイを使う方法ならタップ数によらず定数回の計算で畳み込みができるので 1 サンプルあたりの計算量が \(O(1)\) に減ります。
\(N\) サンプルの遅延を加えるディレイを用意します。 \(N\) は整数です。
// C++
#include <algorithm>
#include <vector>
template<typename Sample> class IntDelay {
private:
std::vector<Sample> buf;
size_t wptr = 0;
size_t rptr = 0;
public:
IntDelay(size_t size = 65536) : buf(size) {}
void resize(size_t size)
{
buf.resize(size);
wptr = 0;
rptr = 0;
}
void reset() { std::fill(buf.begin(), buf.end(), Sample(0)); }
void setFrames(size_t delayFrames)
{
if (delayFrames >= buf.size()) delayFrames = buf.size();
rptr = wptr - delayFrames;
if (rptr >= buf.size()) rptr += buf.size(); // Unsigned overflow case.
}
Sample process(Sample input)
{
if (++wptr >= buf.size()) wptr -= buf.size();
buf[wptr] = input;
if (++rptr >= buf.size()) rptr -= buf.size();
return buf[rptr];
}
};以下の MovingAverageFilter の実装では、状態変数
sum
を用意して、各サンプルでディレイへの入力を加算、ディレイからの出力を減算します。
sum
をフィルタのタップ数で割った値がフィルタの出力です。
// C++
#include <limits>
template<typename Sample> class MovingAverageFilter {
private:
Sample denom = Sample(1);
Sample sum = 0;
IntDelay<Sample> delay;
public:
void resize(size_t size)
{
delay.resize(size);
}
void reset()
{
sum = 0;
delay.reset();
}
void setFrames(size_t frames)
{
denom = Sample(1) / Sample(frames);
delay.setFrames(frames);
}
// 浮動小数点数の丸めが 0 に向かうように変更した加算。
inline Sample add(Sample lhs, Sample rhs)
{
if (lhs < rhs) std::swap(lhs, rhs);
int expL;
std::frexp(lhs, &expL);
auto &&cut = std::ldexp(float(1), expL - std::numeric_limits<Sample>::digits);
auto &&rounded = rhs - std::fmod(rhs, cut);
return lhs + rounded;
}
// 素朴な実装。
Sample processNaive(Sample input)
{
input *= denom;
sum = (sum + input) - delay.process(input);
return sum;
}
// リミッタ向けの実装。 `input` の範囲が [0, 1] であることを仮定。
Sample process(Sample input)
{
input *= denom;
sum = add(sum, input);
Sample d1 = delay.process(input);
sum = std::max(Sample(0), sum - d1);
return sum;
}
};素朴な実装とリミッタ向けの実装をまとめて掲載しています。
素朴な実装では、浮動小数点数の丸めモードが最も近い偶数への丸めになるときに、誤差によってオーバーシュートが起こります。
C++ では
std::numeric_limits<float>::round_style == std::round_to_nearest
が true のときに最も近い偶数への丸めが行われます。
リミッタ向けの実装では add メソッドで無理やり 0
にむかって丸めることでオーバーシュートを防いでいます。
add メソッドでは、加算時に 2
つの値の小さいほうについて仮数部に乗り切らない部分を切り捨てることで 0
に向かう丸めを実装しています。
C の標準ライブラリ <fenv.h> 、または C++
の標準ライブラリ <cfenv> に丸めのモードを切り替える
fesetround
が用意されています。ターゲットの環境が -inf あるいは 0
に向かう丸めをサポートしているときは、上の add ではなく、
fesetround の使用を推奨します。
丸めについての例として、以下のような 4 ビットの浮動小数点数
1000 と 11.11 の加算を挙げておきます。数字は
2 進数です。
1000
+ 0011.11 // 0.11 が 4 ビットに乗り切らないので丸められる。
---------
1???11.11
に最も近い偶数は 100 なので、加算の結果は
1100 。0.11
が切り捨てられるので、加算の結果は 1011 。Musicdsp.org のページでは、以下のコードのように入力で
1.0 - input 、出力で 1.0 - output
を計算することで浮動小数点数による計算誤差を減らす手順があります。はっきりとは書いていませんが
input の範囲は [0.0, 1.0] のようです。
// C++
template<typename Sample> class MovingAverage {
public:
// ...
Sample process(Sample input) {
input = Sample(1) - input;
sum += input - delay.process(input);
return Sample(1) - sum / delay.buffer.size();
}
};次のようなコードを書いて素朴な実装と比べました。
constexpr size_t nLoop = 300;
constexpr uint32_t size = 100;
MovingAverage<float> av1;
av1.setSize(size);
MovingAverage<float> av2;
av2.setSize(size);
float big = 0.1f;
float small = big;
for (size_t i = 0; i < 23; ++i) small /= 2; // small = big / 2^23.
for (size_t i = 0; i < nLoop; ++i) {
float input = (i / size) % 2 == 0 ? big : small;
av1.process1(input); // 1 から引く手順なし。
av2.process2(input); // 1 から引く手順あり。
}テスト時のコンパイラは Microsoft の cl.exe (Version 19.27.29111 for
x86) を使いました。 /fp:precise と fp:fast
を試しましたが、どちらも同じ値が出ました。
テストでは big と small が 100
サンプルごとに切り替わる信号を移動平均フィルタに入力しています。
テストによって分かった 1 から引く手順ありのときの問題点です。
sum = 0 のときに正しくスムーシングされない。big より 1
大きくなることがある。big = 0.9f で確認。)1 から引く手順なしのときの問題点です。
big = 0.7f と 0.9f で確認。)1 から引く手順ありだと数値誤差による問題が増えるので使わないほうが良さそうです。
1 から引く手順なしでも 0 に近い小さな値が含まれる信号のときは予期しない符号の反転が起こるおそれがあるので注意が必要です。
Bessel フィルタは連続系で群遅延が maximally flat になることが特長のフィルタですが、離散化にバイリニア変換などを使うと周波数が歪むので特長が損なわれます。
Maximally flat はフィルタの専門用語で次の 2 つの性質を持ちます。
SciPy の signal.bessel()
を試します。 SciPy 1.5.2 では signal.bessel()
はバイリニア変換を使っています。
# Python3
import matplotlib.pyplot as plt
import numpy as np
import scipy.signal as signal
order = 4
delay = 512
sos = signal.bessel(order, 2 / (np.pi * delay), norm="delay", output="sos")
sig = np.hstack((np.zeros(delay), np.ones(delay * 2)))
out = signal.sosfilt(sos, sig)
plt.axvline(2 * delay, lw=1, color="black", alpha=0.5, ls="--")
plt.plot(sig, lw=1, color="black", label="Input")
plt.plot(out, lw=1, color="red", label="Bessel")
plt.grid()
plt.legend()
plt.show()出力です。ステップ応答は S 字になりますがオーバーシュートが出ます。
次数の高い伝達関数をそのまま計算すると浮動小数点数による誤差で発散することがあります。そこで 2 次セクション (second order sections, sos) に分割して C++ に移植します。
カットオフ周波数を自由に変更するために、以下の Python3 のコードと、 Neil Robertson さんによる Design IIR Filters Using Cascaded Biquads で紹介されていた手法を組み合わせています。
# Python3
import numpy as np
import scipy.signal as signal
def bessel(order, delay):
z, p, k = signal.besselap(order, norm="delay")
z, p, k = signal.lp2lp_zpk(z, p, k, delay)
z, p, k, _ = signal.cont2discrete([z, p, k], 1, method="bilinear")
return signal.zpk2sos(z, p, k)コードの z, p, k は zero, pole, gain
の略です。
Bessel フィルタは極だけでゼロは一つもありません。このようなフィルタは全極フィルタ (all-pole filter) と呼ばれています。極は伝達関数の分母の多項式の根を求めることで計算できます。
今回は root-finding
アルゴリズムを評価、実装する手間を省きたかったので signal.besselap()
から得られた極をそのまま定数として使うことにしました。
# Python3
import numpy as np
import scipy.signal as signal
z, p, k = signal.besselap(4, norm="delay") # 4 次。
print(p.tolist())整形した出力です。
[
(-2.1037893971796273+2.6574180418567526j), # p1
(-2.8962106028203722+0.8672341289345038j), # p2
(-2.8962106028203722-0.8672341289345038j), # p2 の複素共役
(-2.1037893971796273-2.6574180418567526j) # p1 の複素共役
]signal.lp2lp_zpk()
はローパスのアナログプロトタイプのカットオフ周波数を設定する関数です。以下はエラー処理などを簡略化した
SciPy 1.5.2 での実装の写しです。
# Python3
def lp2lp_zpk(z, p, k, wo=1.0):
degree = len(p) - len(z)
z_lp = wo * z
p_lp = wo * p
k_lp = k * wo**degree
return z_lp, p_lp, k_lpBessel フィルタはゼロが無く、ゲインは別の方法で計算するので
z_lp と k_lp は C++
のコードでは計算していません。
アナログプロトタイプからの離散化にはバイリニア変換を使います。次のバイリニア変換の式の \(s\) に連続系の極を代入することで、離散フィルタの極に変換できます。
\[ z = \frac{2 f_s + s}{2 f_s - s} \]
signal.besselap() から得られた極は \(f_s = 1\)
とすると正しく変換できました。
\(N\) 次の全極フィルタの伝達関数は次の形になります。 \(\hat{p}\) はアナログフィルタの極です。
\[ H(z) = \frac{1}{\displaystyle \prod_{i=1}^{N} (s - \hat{p}_i)} \]
\(s\) について解いたバイリニア変換の式です。
\[ s = 2 f_s \frac{1 - z^{-1}}{1 + z^{-1}} \]
\(s\) について解いたバイリニア変換の式を全極フィルタの伝達関数に代入してまとめると次の形になります。 \(p\) は離散フィルタの極、 \(K\) はゲインです。
\[ H(z) = K \frac{(z + 1)^N}{\displaystyle \prod_{i=1}^{N} (z - p_i)} \]
次数が偶数の Bessel フィルタの極は複素共役の組 (conjugated pairs) になります。例えば 4 次なら \((p_1, p_2, p_2^*, p_1^*)\) という 4 つの極が出てきます。 \(^*\) は複素共役の演算子です。 2 次セクションを作るときは複素共役の組となる極を使うことで計算を簡略化できます。
\[ \begin{aligned} H(z) &= \prod_{i=1}^{N / 2} K_i \frac{(z + 1)^2}{(z - p_i)(z - p_i^*)} \\ &= \prod_{i=1}^{N / 2} K_i \frac{1 + 2 z^{-1} + z^{-2}}{ 1 - 2\,\mathrm{Re}(p_i) z^{-1} + |p_i|^2 z^{-2} } \end{aligned} \]
ゲインの計算式を出すために 2 次セクションを一つだけ取り出します。
\[ H(z) = K_i \frac{1 + 2 z^{-1} + z^{-2}}{1 - 2\,\mathrm{Re}(p_i) z^{-1} + |p_i|^2 z^{-2}} \]
\(\omega = 0\) のときに振幅特性 が 1 となるゲイン \(K_i\) を求めます。振幅特性は \(z = e^{j \omega}\) と代入すると計算できますが、ここでは \(\omega = 0\) なので \(z = 1\) と簡略化できます。
\[ H(1) = 1 = K_i \frac{1 + 2 + 1}{1 - 2\,\mathrm{Re}(p_i) + |p_i|^2} \]
\(K_i\) について解きます。
\[ K_i = \frac{1 - 2\,\mathrm{Re}(p_i) + |p_i|^2}{4} \]
すべての 2 次セクションのゲイン \(K_i\) を掛け合わせることで、フィルタ全体のゲイン \(K\) が計算できます。
\[ K = \prod_{i=1}^N K_i \]
C++17 のフラグを立ててコンパイルしています。
// C++
#include <array>
#include <complex>
template<typename Sample> struct Bessel4 {
// float はディレイ時間が短いときだけ使える (delayInSamples <~ 1000) 。
// それ以外のときは double を使うこと。
constexpr static uint8_t halfDegree = 2; // 4 の半分。
// 複素共役の極は無くても計算できる。
constexpr static std::array<std::complex<Sample>, halfDegree> analogPole{{
{Sample(-2.1037893971796273), Sample(+2.6574180418567526)},
{Sample(-2.8962106028203722), Sample(+0.8672341289345038)},
}};
std::array<Sample, 2> x0{};
std::array<Sample, 2> x1{};
std::array<Sample, 2> x2{};
std::array<Sample, 2> y0{};
std::array<Sample, 2> y1{};
std::array<Sample, 2> y2{};
std::array<std::array<Sample, 2>, halfDegree> co; // フィルタ係数。
Sample gain = 1;
Bessel4()
{
for (auto &coef : co) coef.fill(0);
}
void reset(Sample value = 0)
{
x0.fill(value);
x1.fill(value);
x2.fill(value);
y0.fill(value);
y1.fill(value);
y2.fill(value);
}
void setDelay(Sample delayInSamples)
{
auto wo = Sample(2) / delayInSamples; // 遅延サンプル数を周波数に変換。
gain = Sample(1);
for (uint8_t i = 0; i < co.size(); ++i) {
std::complex<Sample> pole = wo * analogPole[i]; // カットオフ周波数の適用。
pole = (Sample(2) + pole) / (Sample(2) - pole); // バイリニア変換。
co[i][0] = Sample(-2) * pole.real();
co[i][1] = std::norm(pole);
gain *= (Sample(1) + co[i][0] + co[i][1]) / Sample(4);
}
}
Sample process(Sample input)
{
x0[0] = input;
for (uint8_t i = 0; i < halfDegree; ++i) {
y0[i]
= x0[i]
+ Sample(2) * x1[i]
+ x2[i]
- co[i][0] * y1[i]
- co[i][1] * y2[i];
x2[i] = x1[i];
x1[i] = x0[i];
y2[i] = y1[i];
y1[i] = y0[i];
if (i + 1 < halfDegree) x0[i + 1] = y0[i];
}
return gain * y0[1];
}
};Thiran ローパスフィルタは群遅延が maximally flat になるように設計されたフィルタです。
Thiran ローパスフィルタの伝達関数です。
\[ H(z) = \frac{2n!}{n!} \, \frac{1}{\displaystyle \prod_{i = n + 1}^{2n} (2 \tau + i)} \, \frac{1}{\displaystyle \sum_{k=0}^n \left( (-1)^k \binom{n}{k} \prod_{i=0}^n \dfrac{2 \tau + i}{2 \tau + k + i} \right) z^{-k} } \]
分母の因数分解は無理そうなので、 2
次セクションに分割するなら多項式の根を探す (root-finding)
アルゴリズムを使って数値的に計算するしかなさそうです。ここでは SciPy
の signal.tf2sos()
を使っています。 C++ では Boost
の root-finding が使えそうです。
ステップ応答を確認します。
# Python3
import numpy as np
import scipy.signal as signal
import scipy.special as special
import matplotlib.pyplot as plt
def thiranLowpass(n, τ):
"""
n: Order of filter.
τ: Desired delay in samples.
"""
a = np.empty(n + 1)
for k in range(n + 1):
i = np.arange(n + 1)
a[k] = (-1)**k * special.binom(n, k) * np.prod((2 * τ + i) / (2 * τ + k + i))
gain_numer = special.factorial(2 * n, exact=True) / special.factorial(n, exact=True)
gain_denom = np.prod(2 * τ + np.arange(n + 1, 2 * n + 1))
b = np.zeros_like(a)
b[0] = gain_numer / gain_denom
return (b, a)
order = 4
delay = 512
b, a = thiranLowpass(order, delay / 2)
sos = signal.tf2sos(b, a)
sig = np.hstack((np.zeros(delay), np.ones(delay * 2)))
out = signal.sosfilt(sos, sig)
plt.axvline(2 * delay, lw=1, color="black", alpha=0.5, ls="--")
plt.plot(sig, lw=1, color="black", label="Input")
plt.plot(out, lw=1, color="red", label="Thiran")
plt.grid()
plt.legend()
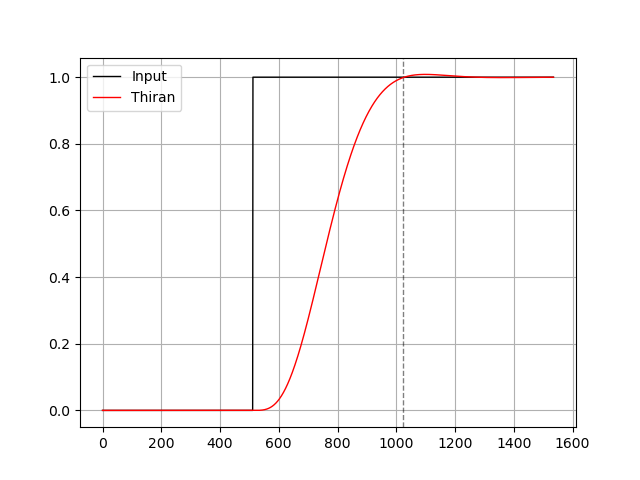
plt.show()出力です。オーバーシュートが出ています。バイリニア変換した Bessel フィルタと同じに見えます。
ゲインの値を定義通りに計算すると delay
の値によってはステップ応答が 1
から少しずれた値に収束することがあります。 1 に収束させるときは signal.freqz()
の値からゲインを計算できます。
# Python3
def thiranLowpassFixedGain(n, τ):
a = np.empty(n + 1)
for k in range(n + 1):
i = np.arange(n + 1)
a[k] = (-1)**k * special.binom(n, k) * np.prod((2 * τ + i) / (2 * τ + k + i))
freq, resp = signal.freqz(1, a, worN=1)
b = np.zeros_like(a)
b[0] = 1 / resp.real
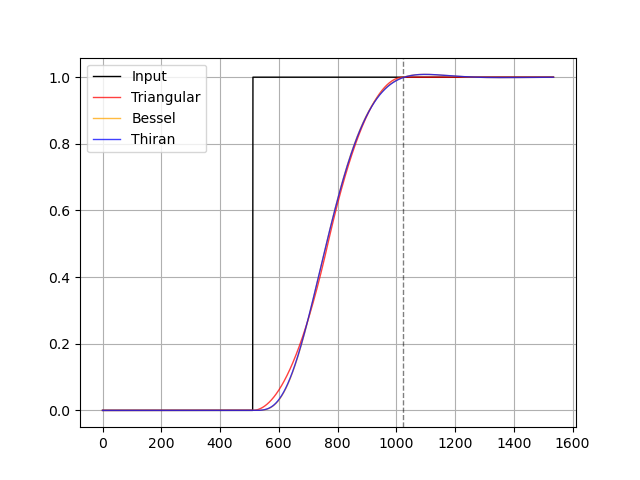
return (b, a)ここまでに紹介した 3 つのフィルタのステップ応答を比較します。
Bessel フィルタと Thiran ローパスフィルタのステップ応答はほとんど同じで重なっています。
離散系で S 字のステップ応答が欲しいときは、オーバーシュートがなく、計算も速くて簡単な移動平均の重ね掛けを使えばよさそうです。
バイリニア変換した Bessel フィルタは、オーバーシュートがあり、移動平均の重ね掛けと比べると計算が重いですが、メモリの使用量が少ないという利点があります。移動平均の重ね掛けは遷移時間と同じサンプル数のメモリが必要です。
Thiran ローパスフィルタはバイリニア変換した Bessel フィルタとほとんど同じですが、 2 次セクションに分割できないので使いどころはなさそうです。
オーバーシュートせずにステップ応答が S 字を描くフィルタとしては、フィルタ係数がすべて正の値となる FIR フィルタも使えます。ただし、遷移時間が長くなると FIR フィルタのタップ数が増える分だけ計算が重たくなります。フィルタ係数は Wikipedia の窓関数の記事からいろいろな曲線が選べます。
![]() から <image> タグに変更。<cfenv>
に関する記載を追加。