何かあれば GitHub のリポジトリに issue を作るか ryukau@gmail.com までお気軽にどうぞ。
Update: 2025-12-28
Kleimola と Valimaki による Reducing aliasing from synthetic audio signals using polynomial transition regions で紹介されていた PTR という方法を使ったオシレータを試します。
PTR (Polynomial Transition Regions) は DPW (Differenciated Polynomial Waveform) という方法に基づいたオシレータの計算方法です。
DPW と PTR では、まず波形関数に連続領域でローパスフィルタをかけた式を求めます。そして離散領域でローパスフィルタがかかった波形の式を計算して離散ハイパスフィルタに通すことでエイリアシングが低減された出力が得られるという手法です。 DPW と PTR では 1 次のローパスフィルタと 1 次の離散ハイパスフィルタを使っているので、計算式の次数が 1 増えるごとにエイリアシングによる折り返しノイズが 6dB 低減されます。
PTR の論文では 3 次までの鋸歯波の計算式が掲載されています。ここでは 4 次以降の計算式と、鋸歯波以外の計算式を求めています。
Python3 のコードでは NumPy 、 matplotlib 、 PySoundFile を使っています。
Maxima のコードは wxMaxima にコピペすれば動きます。
次の図は鋸歯波の \(f(x)\) と PTR で計算する遷移領域のイメージ図です。
式の導出の手順は次のようになります。
一般的な DPW の式です。 \(N\) は任意の次数、 \(f(x)\) は波形関数です。
\[ \mathtt{DPW}(N, f(x)) = J^{N - 1} f(x) \]
ここでは \(J\) を積分演算子として定義しています。
\[ \begin{aligned} J f(x) &= \int f(x) \,dx\\ J^2 f(x) &= \iint f(x) \,d^2x\\ J^3 f(x) &= \iiint f(x) \,d^3x\\ &\vdots \end{aligned} \]
鋸歯波では \(f(x) = x\) とします。この式は \([-1, 1]\) の範囲で 1 周期分の鋸歯波になります。 wxMaxima でプロットします。
plot2d(x, [x, -1, 1])$\(f(x) = x\) としたときの DPW の式です。
\[ \begin{alignedat}{2} \mathtt{DPWSaw}(2, x) &= J^1 f(x) &&= \frac{x^2}{2} + C_1\\ \mathtt{DPWSaw}(3, x) &= J^2 f(x) = J \left( \frac{x^2}{2} + C_1 \right) &&= \frac{x^3}{6} + C_1 x + C_2\\ \mathtt{DPWSaw}(4, x) &= J^3 f(x) = J \left( \frac{x^3}{6} + C_1 x + C_2 \right) &&= \frac{x^4}{24} + C_1 \frac{x^2}{2} + C_2 x + C_3\\ &\vdots \end{alignedat} \]
出てきた積分定数 \(C_i\) に値を代入します。まず \(x\) が乗じられていない積分定数を \(0\) にします。次に波形関数 \(f\) の性質から適当な値を見つけて \(x\) に代入して解くことで適切な値を求めることができます。鋸歯波では \(\mathtt{DPWSaw}(N, 1) = \mathtt{DPWSaw}(N, -1)\) と置くといいようです。この手続きを \(N = 1\) から順に繰り返すことで高次の DPW の積分定数を求めることができます。
\[ \begin{alignedat}{2} \mathtt{DPWSaw}(2, x) &= \frac{x^2}{2} + 0\\ \\ \mathtt{DPWSaw}(3, 1) &= \mathtt{DPWSaw}(3, -1)\\ \frac{(1)^3}{6} + C_1 (1) + 0 &= \frac{(-1)^3}{6} + C_1 (-1) + 0\\ C_1 &= -\frac{1}{6}\\ \\ \mathtt{DPWSaw}(4, 1) &= \mathtt{DPWSaw}(4, -1)\\ \frac{(1)^4}{24} + \frac{1}{6} \frac{(1)^2}{2} + C_2 (1) + 0 &= \frac{(-1)^4}{24} + \frac{1}{6} \frac{(-1)^2}{2} + C_2 (-1) + 0\\ C_2 &= 0\\ \\ &\vdots \end{alignedat} \]
積分定数 \(C_i\) は \(i\) が偶数のときは 0 になるようです。
得られた \(C_i\) を \(\mathtt{DPWSaw}(N, x)\) に代入します。このとき、 \(C_{N-1}\) は 0 にします。
\[ \begin{alignedat}{2} \mathtt{DPWSaw}(2, x) &= \frac{x^2}{2} + 0 &&= \frac{x^2}{2}\\ \mathtt{DPWSaw}(3, x) &= \frac{x^3}{6} + \left( -\frac{1}{6} \right) x + 0 &&= \frac{x^3}{6} - \frac{x}{6}\\ \mathtt{DPWSaw}(4, x) &= \frac{x^4}{24} + \left( -\frac{1}{6} \right) \frac{x^2}{2} + (0) x + 0 &&= \frac{x^4}{24} - \frac{x^2}{12}\\ &\vdots \end{alignedat} \]
後で音量を補正するので、最も次数の高い項の係数が 1 になるように正規化します。
\[ \begin{aligned} \mathtt{DPWSaw}(2, x) &= x^2\\ \mathtt{DPWSaw}(3, x) &= x^3 - x\\ \mathtt{DPWSaw}(4, x) &= x^4 - 2 x^2\\ &\vdots \end{aligned} \]
この式は DPW 論文の Table I で紹介されている式にあたります。
\(x\) に素朴な鋸歯波 \(s(n)\) を代入して、 1 次差分を \(N\) 回繰り返し、適切な音量になるようにスケーリング係数 \(c(N)\) をかけ合わせることで出力信号が得られます。
\[ \begin{aligned} T &= \frac{f_0}{f_s}\\ \phi(n) &= n T \bmod 1.0\\ s(n) &= 2 \phi(n) - 1\\ c(N) &= \frac{1}{(2T)^{N - 1} N!}\\ \mathtt{output}(N, n) &= c(N) \nabla^{N - 1} \mathtt{DPWSaw}(N, s(n)) \end{aligned} \]
\(n\) は経過したサンプル数、 \(f_0\) は生成する信号の周波数、 \(f_s\) はサンプリング周波数です。
ここでの \(\nabla\) は 1 サンプル前の信号との差分を計算する演算子です。 PTR 論文で定義されています。
\[ \nabla x(n) = x(n) - x(n - 1) \]
2 次の差分は次のようになります。
\[ \begin{aligned} \nabla^2 x(n) &= \nabla (x(n) - x(n - 1))\\ &= \nabla x(n) - \nabla x(n - 1)\\ &= (x(n) - x(n - 1)) - (x(n - 1) - x(n - 2))\\ &= x(n) - 2 x(n - 1) + x(n - 2)\\ \end{aligned} \]
3 次の差分です。
\[ \begin{aligned} \nabla^3 x(n) &= \nabla (\nabla^2 x(n))\\ &= \nabla (x(n) - 2 x(n - 1) + x(n - 2)\\ &= x(n) - 3 x(n - 1) + 3(n - 2) - x(n - 3)\\ \end{aligned} \]
\(\nabla^N\) の係数はパスカルの三角形の \(N\) 行目と一致します。また、正負の符号は前の項から順に反転を繰り返しています。これらの性質を使って \(\nabla^N x(n)\) は次のように書けます。
\[ \nabla^N x(n) = \sum_{k=0}^{N} (-1)^{N} \binom{N}{k} x(n - k) \]
DPW と PTR では \(\nabla\) の計算方法が異なります。 DPW では過去の計算結果を使いますが、 PTR では過去の計算結果に依存せずに計算できるように、さらに式を変形します。
例として \(\mathtt{output}(3, n)\) から PTR の式を求めます。 \(\mathtt{output}(3, n)\) を展開します。
\[ \begin{aligned} \mathtt{output}(3, n) &= \frac{1}{(2 T)^2 3!} \nabla^2 \mathtt{DPWSaw}(3, s(n))\\ &= \frac{\nabla^2 (s^3(n) - s(n))}{24T^2}\\ &= \frac{(s^3(n) - 2 s^3(n - 1) + s^3(n - 2)) - (s(n) - 2 s(n - 1) + s(n - 2))}{24T}\\ \end{aligned} \]
\(s(n),\ s(n - 1),\ s(n - 2)\) に含まれる \(\phi(n)\) には \(\bmod\) が含まれているので場合分けが出てきます。ここでは \(n T < 0\) のとき \(\phi(n) = n T + h\) 、 \(n T \geq 0\) のとき \(\phi(n) = n T\) としています。 \(h\) は遷移領域の高さです。ハードシンクをかけるときは 1 以外の値になることがあります。
\[ \begin{matrix} \begin{aligned} \text{if}\enspace 0 \leq \phi(n) &< T:\\ s(n) &= 2 n T - 1\\ s(n - 1) &= 2 ((n - 1) T + h) - 1\\ s(n - 2) &= 2 ((n - 2) T + h) - 1\\ \end{aligned} &\quad \begin{aligned} \text{if}\enspace T \leq \phi(n) &< 2T:\\ s(n) &= 2 n T - 1\\ s(n - 1) &= 2 (n - 1) T - 1\\ s(n - 2) &= 2 ((n - 2) T + h) - 1\\ \end{aligned} &\quad \begin{aligned} \text{if}\enspace 2T \leq \phi(n) &:\\ s(n) &= 2 n T - 1\\ s(n - 1) &= 2 (n - 1) T - 1\\ s(n - 2) &= 2 (n - 2) T - 1\\ \end{aligned} \end{matrix} \]
\(\phi(n)\) は範囲が \([0, 1)\) に正規化された位相、 \(T\) は 1 サンプルの間に進む位相を表しています。
次の図は遷移領域の場合分けの範囲を表しています。
これらの式を代入することで遷移領域内の計算式が得られます。 Maxima を使います。
N: 3;
for k: 1 thru N do (
phi(n) := if n > 'n - k then n * T else n * T + h,
s(n) := 2 * phi(n) - 1,
eq: (
(s(n)^3 - 2 * s(n - 1)^3 + s(n - 2)^3) /* ∇^2 s^3(n) */
- (s(n) - 2 * s(n - 1) + s(n - 2)) /* ∇^2 (-s(n)) */
) / 24 / T^2,
condition:
if k = N then (k - 1) * T <= phi
else (k - 1) * T <= phi and phi < k * T,
disp([condition, expand(eq)])
);整形した出力です。
\[ \mathtt{PTRSaw}(3, n) = \begin{cases} \text{if}\enspace 0 \leq \phi(n) < T, &\quad -h {{n}^{2}}-\dfrac{{{h}^{2}} n}{T}+\dfrac{h n}{T}+2 T n-\dfrac{{{h}^{3}}}{3 {{T}^{2}}}+\dfrac{{{h}^{2}}}{2 {{T}^{2}}}-\dfrac{h}{6 {{T}^{2}}}+2 h-2 T-1\\\\ \text{if}\enspace T \leq \phi(n) < 2 T, &\quad h {{n}^{2}}+\dfrac{{{h}^{2}} n}{T}-\dfrac{h n}{T}-4 h n+2 T n+\dfrac{{{h}^{3}}}{3 {{T}^{2}}}-\dfrac{2 {{h}^{2}}}{T}-\dfrac{{{h}^{2}}}{2 {{T}^{2}}}+\dfrac{2 h}{T}+\dfrac{h}{6 {{T}^{2}}}+4 h-2 T-1\\\\ \text{if}\enspace 2 T \leq \phi(n), &\quad 2 T n-2 T-1 \end{cases} \]
PTR の論文で紹介されている式は \(h / T\) を含む項がすべて取り除かれた式になっています。
\[ \mathtt{PTRSaw}(3, n) = \begin{cases} \text{if}\ \ 0 \leq \phi(n) < T,\quad&-h\, {{n}^{2}}+2 T n+2 h-2 T-1\\\\ \text{if}\ \ T \leq \phi(n) < 2 T,\quad&h\, {{n}^{2}}-4 h n+2 T n+4 h-2 T-1\\\\ \text{if}\ \ 2 T \leq \phi(n),\quad&2 T n-2 T-1 \end{cases} \]
\(h / T\) を含む式を使うと遷移領域の値が大きくなりすぎるようです。実用上は \(h / T\) を含まない式を使うほうが良さそうです。 次のリンクから実装したコードが読めます。
ここまでの式変形を Maxima で実装して、より高次の PTR の式を導出しました。また、導出した式を Python3 のコードにしました。コードは量が多くなったので別ページに分けました。
\([-1, 1]\) の範囲で 1 周期分の三角波を生成する波形関数です。
\[ f_{t}(x) = 1 - 2 |x| \]
wxMaxima でプロットします。
plot2d(1 - 2 * abs(x), [x, -1, 1])$DPW 論文によると、三角波の波形関数を積分した関数 \(\mathtt{DPWTri}(N, x)\) は次のようになっています。 \(N\) は積分した回数です。
\[ \begin{aligned} \mathtt{DPWTri}(N, x) &= \left( \sum_{i \geq 1,\,i\ \text{is odd}}^{N-1} a_i x^i \right) + g(N, x)\\ g(i, x) &= \begin{cases} x^i, &\quad \text{if}\enspace i \ \ \text{is odd},\\ x^{i-1} |x|, &\quad \text{if}\enspace i \ \ \text{is even}.\\ \end{cases} \end{aligned} \]
定数 \(a_i\) が決まれば計算できる式になります。例として \(\mathtt{DPWTri}(4, x)\) のときの定数 \(a_i\) を求めます。
\[ \mathtt{DPWTri}(4, x) = a_1 x + a_3 x^3 + x^3 |x| \]
\(N-1\) 回まで微分した式を求めます。 \(x^{i - 1} |x|\) の項は \(x^i\) と置き換えていいようです。 \(D\) は微分の演算を表しています。
\[ \begin{aligned} \mathtt{DPWTri}(4, x) &= a_1 x + a_3 x^3 + x^4\\ D f_{t}(4, x) &= a_1 + 3 a_3 x^2 + 4 x^3\\ D^2 f_{t}(4, x) &= 6 a_3 x + 12 x^2\\ D^3 f_{t}(4, x) &= 6 a_3 + 24 x\\ \end{aligned} \]
方程式 \(D^i f_{t}(N, 0.5) = 0\) を微分した回数が大きい式から順に解いていきます。
\[ \begin{aligned} D^3 f_{t}(4, 0.5) &= 0\\ 6 a_3 + 24 (0.5) &= 0\\ a_3 &= -2\\ \\ D f_{t}(4, x) &= 0\\ a_1 + 3 (-2) (0.5)^2 + 4 (0.5)^3 &= 0\\ a_1 &= 1\\ \\ \mathtt{DPWTri}(4, x) &= x - 2 x^3 + x^3 |x| \end{aligned} \]
鋸歯波の PTR の式を流用して三角波の PTR の式が書けます。 \(N\) が偶数のときと奇数のときで場合分けがあります。
\[ \begin{aligned} s_{t}(N, n) &= \begin{cases} 1/2 - |1 - 2 nT|& \text{if}\ N\ \text{is odd.}\\ 1 - 2 n T& \text{if}\ N\ \text{is even.} \end{cases}\\ c_{t}(N) &= \frac{2}{(2T)^{N - 1} N!}\\ \mathtt{PTRTri}(N, n) &= c_{t}(N) \nabla^{N - 1} \mathtt{DPWTri}(N, s_{t}(N, n)) \end{aligned} \]
\(s_{t}(N, n)\) は DPW の論文の Table III を参考にして少し変更しています。 \(1 - 2 nT\) を \(2 nT - 1\) にすると波形の符号が反転します。
DPW 論文によると、三角波のスケーリング係数 \(c_{t}(N)\) は \(2 c(N)\) となるようです。
あとは鋸歯波と同様に \(\nabla\) を展開して場合分けを行うことで PTR の式が得られます。実装は長いので別ページに掲載しています。
積分定数を決められるように、少しずらしたランプ関数を使います。
\[ f_{tpz}(x) = \begin{cases} 0, & \text{if}\ x < -1,\\ x + 1, & \text{if}\ x \geq -1. \end{cases} \]
Maxima でプロットします。
plot2d(if x < -1 then 0 else x + 1, [x, -2, 2])$式変形は鋸歯波とほとんど同じです。 \(f_{r}(x) = x + 1\) として積分します。
\[ \begin{alignedat}{2} \mathtt{DPWRamp}(2, x) &= J^1 f_{r}(x) &&= \frac{x^2}{2} + x + C_1\\ \mathtt{DPWRamp}(3, x) &= J^2 f_{r}(x) &&= \frac{x^3}{6} + \frac{x^2}{2} + C_1 x + C_2\\ \mathtt{DPWRamp}(4, x) &= J^3 f_{r}(x) &&= \frac{x^4}{24} + \frac{x^3}{6} + C_1 \frac{x^2}{2} + C_2 x + C_3\\ &\vdots \end{alignedat} \]
積分定数を決めるときの方程式を \(\mathtt{DPWRamp}(N, -1) = 0\) に変えます。
\[ \begin{alignedat}{2} \mathtt{DPWRamp}(2, x) &= \frac{x^2}{2} + x + 0\\ \\ \mathtt{DPWRamp}(3, -1) &= 0\\ \frac{(-1)^3}{6} + \frac{(-1)^2}{2} + C_1 (-1) + 0 &= 0\\ C_1 &= \frac{1}{3}\\ \\ \mathtt{DPWRamp}(4, -1) &= 0\\ \frac{(-1)^4}{24} + \frac{(-1)^3}{6} + \frac{1}{3} \frac{(-1)^2}{2} + C_2 (-1) + 0 &= 0\\ C_2 &= \frac{1}{24}\\ \\ &\vdots \end{alignedat} \]
積分定数を \(\mathtt{DPWRamp}(N, x)\) に代入して、最も次数の高い項の係数が 1 になるように正規化します。
\[ \begin{aligned} \mathtt{DPWRamp}(2, x) &= x^2 + 2 x\\ \mathtt{DPWRamp}(3, x) &= x^3 + 3 x^2 + 2 x\\ \mathtt{DPWRamp}(4, x) &= x^4 + 4 x^3 + 4 x^2 + x\\ &\vdots \end{aligned} \]
得られた \(\mathtt{DPWRamp}\) を使って出力信号の式を立てます。
\[ \begin{aligned} s_{r}(n) &= \begin{cases} 0 & \text{if}\ n < 0,\\ 2 n T - 1& \text{if}\ n \geq 0. \end{cases}\\ c(N) &= \frac{1}{(2T)^{N - 1} N!}\\ \mathtt{output}(N, n) &= c(N) \nabla^{N - 1} \mathtt{DPWRamp}(N, s_{r}(n)) \end{aligned} \]
スケーリング係数は鋸歯波と同じ \(c(N)\) を使います。
Maxima と Python3 のコードへのリンクです。
ランプ関数を 1 階微分するとステップ関数になります。
\[ \begin{alignedat}{2} \mathtt{DPWStep}(2, x) &= D(\mathtt{DPWRamp}(2, x)) &&= 2 x + 2\\ \mathtt{DPWStep}(3, x) &= D(\mathtt{DPWRamp}(3, x)) &&= 3 x^2 + 6 x + 2\\ \mathtt{DPWStep}(4, x) &= D(\mathtt{DPWRamp}(4, x)) &&= 4 x^3 + 12 x^2 + 8 x + 1\\ &\vdots \end{alignedat} \]
残りの式変形はランプ関数と同じです。
Maxima と Python3 のコードへのリンクです。
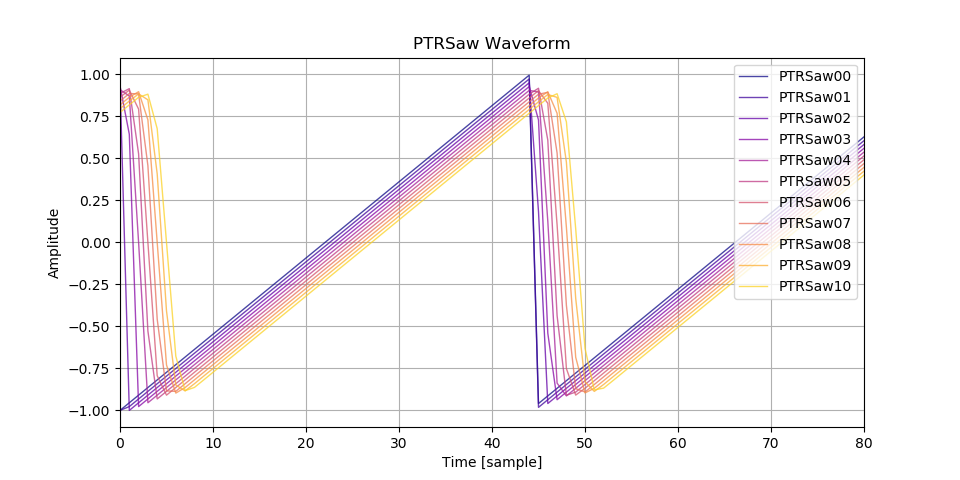
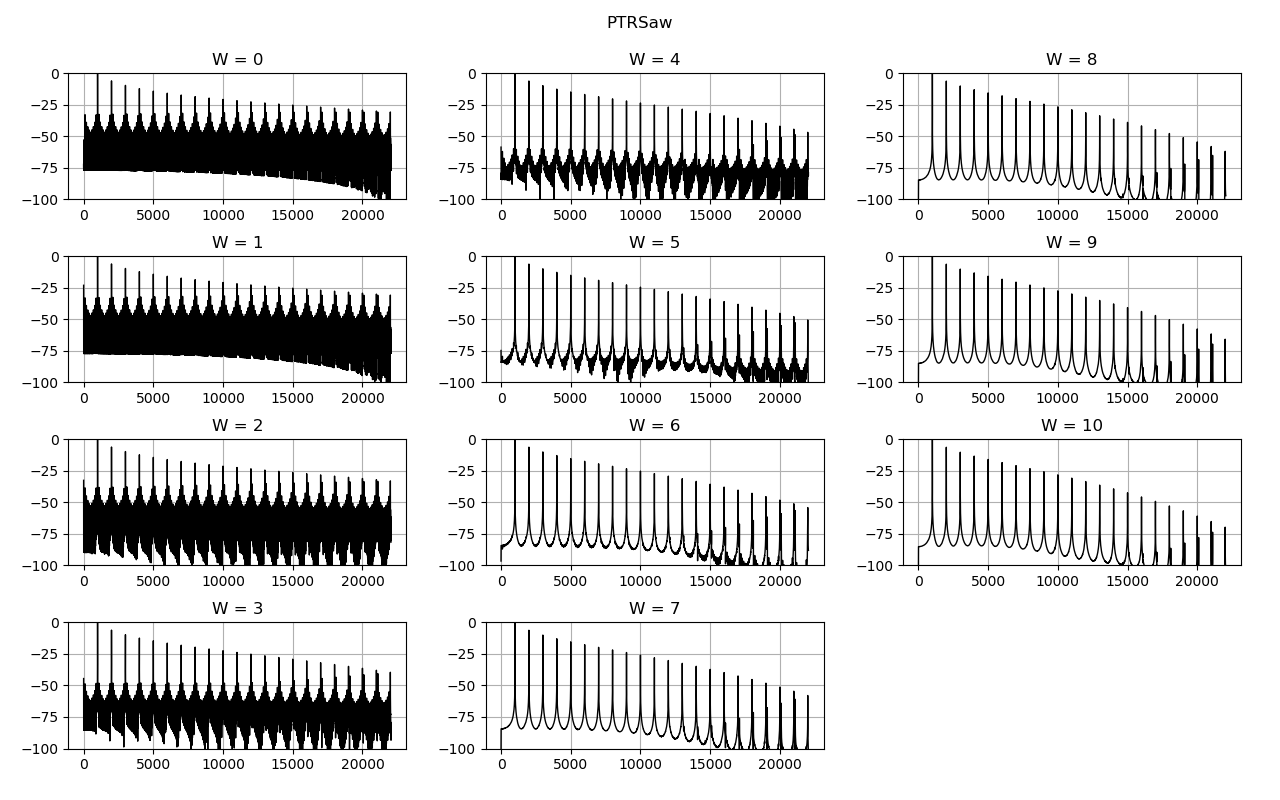
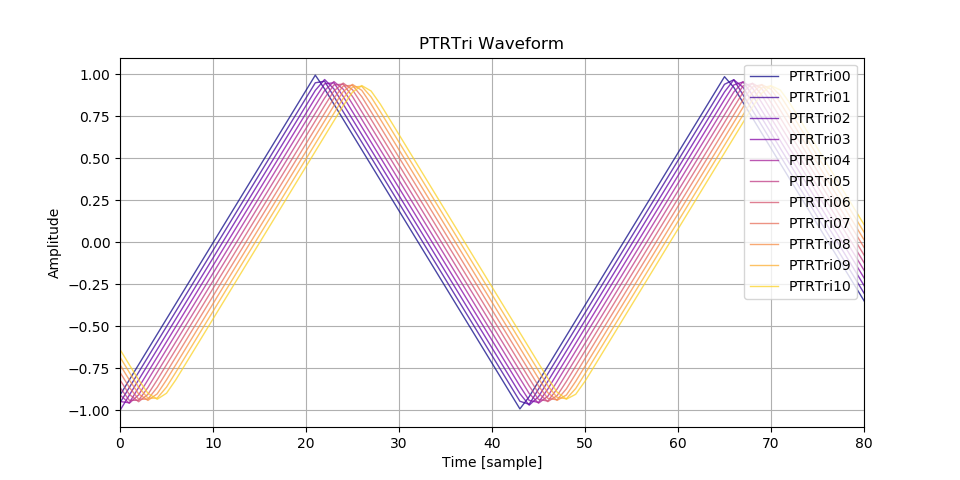
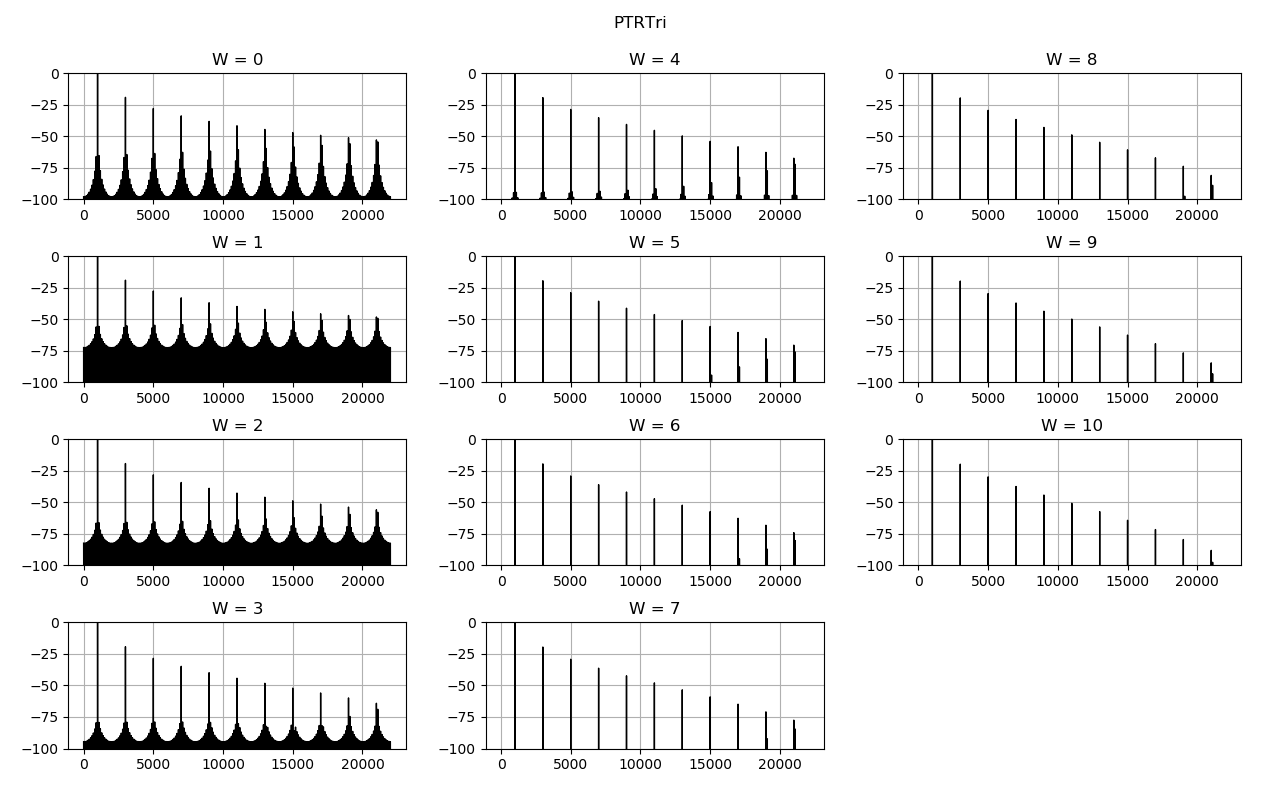
PTR 論文では次数の区別に、 \(\nabla\) による差分の回数 \(W = N - 1\) を使っています。以下で使う PTR[波形][番号] という名前の番号は \(W\) です。
プロットに使ったコードへのリンクです。
波形の比較です。
スペクトラムの比較です。横軸は周波数、縦軸はゲイン [dB] です。
1000 Hz でレンダリングした音です。
鋸歯波にハードシンクをかけた音です。次数が上がったときのオーバーシュートが面白いです。
三角波のレンダリングは、次の図のように上りと下りの 2 つの区間に分けて行いました。図の下側の矢印は位相を進める方向を表しています。
波形の比較です。
スペクトラムの比較です。横軸は周波数、縦軸はゲイン [dB] です。
1000 Hz でレンダリングした音です。 \(W = 3\) 以降は耳で聞いても違いが分かりません。
ランプ関数は 4 つの区間に分けてレンダリングしました。
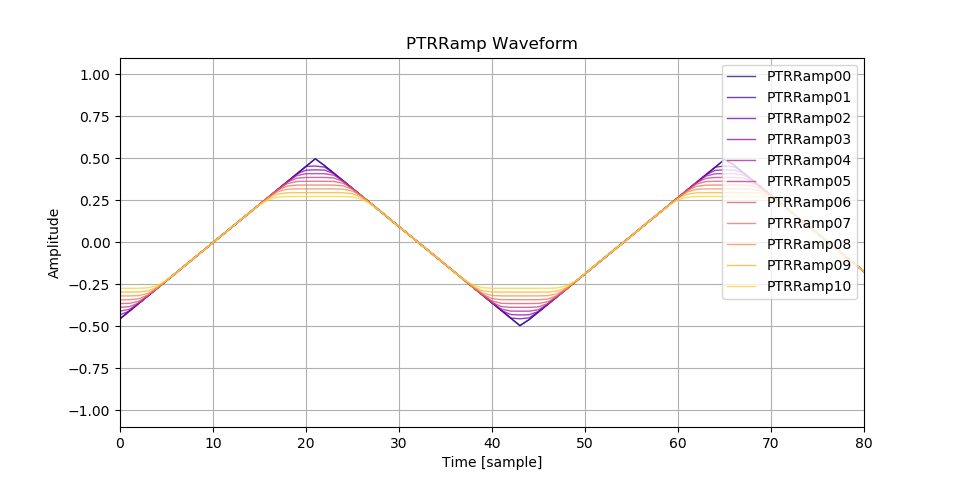
波形の比較です。 \(N \leq 1\) では Maxima で求めた式がそのまま使えないようです。
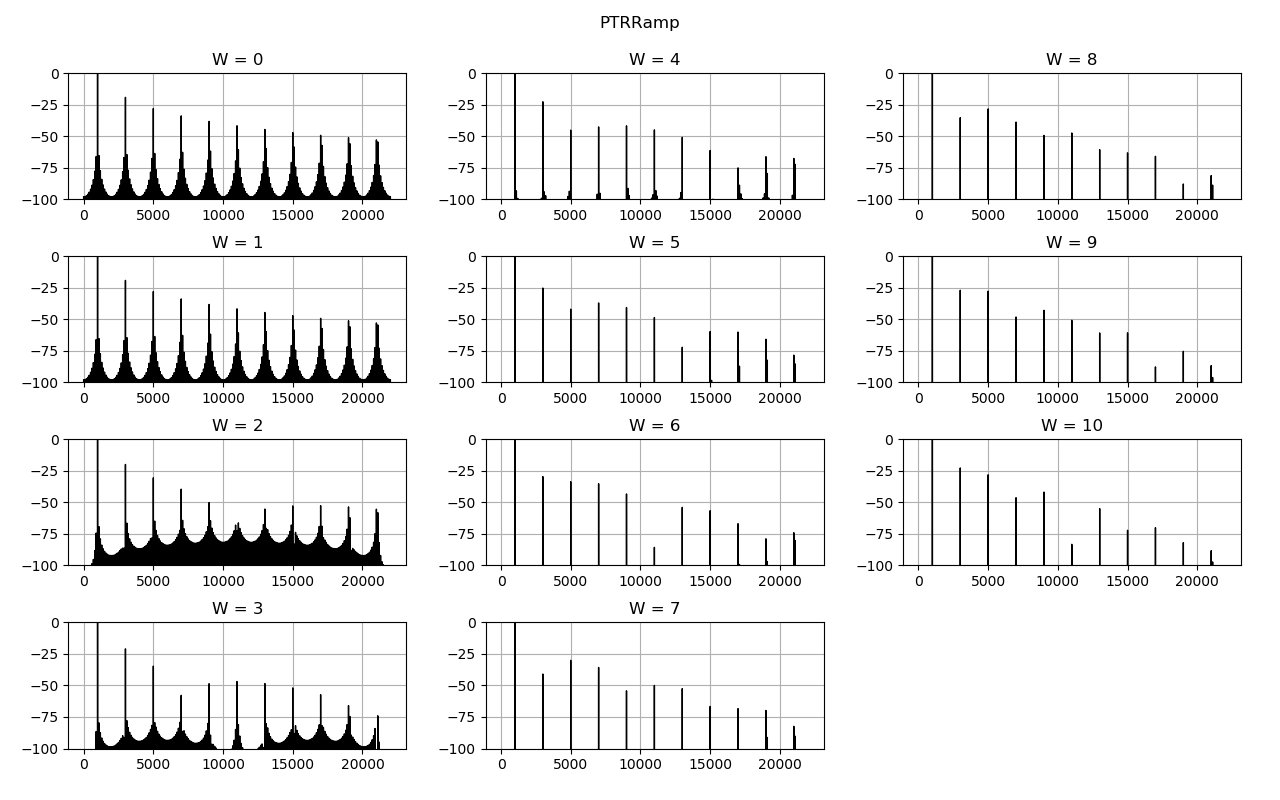
スペクトラムの比較です。横軸は周波数、縦軸はゲイン [dB] です。 \(N\) の値によって波形が別物になっているので、あまり意味のあるデータではないです。
1000 Hz でレンダリングした音です。
ステップ関数のレンダリングは三角波と同様です。
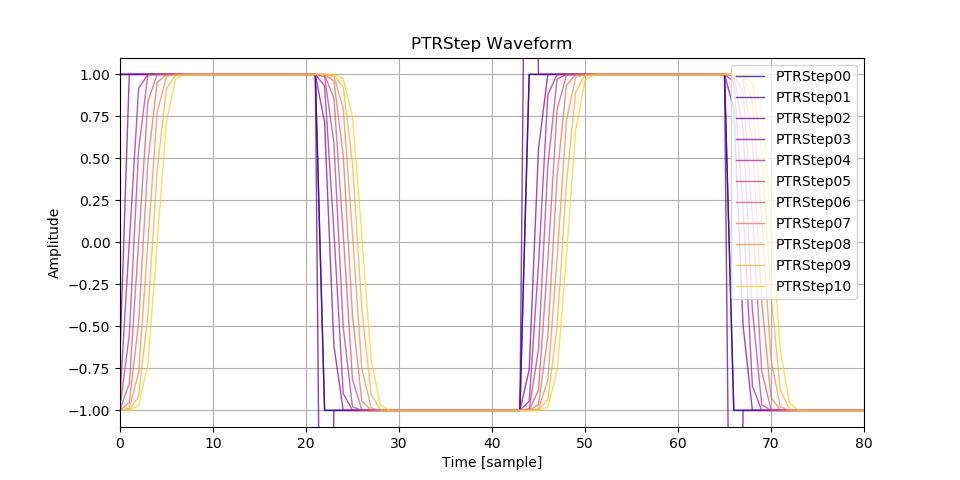
波形の比較です。 PTRStep02 はエッジの部分がおかしくなっています。
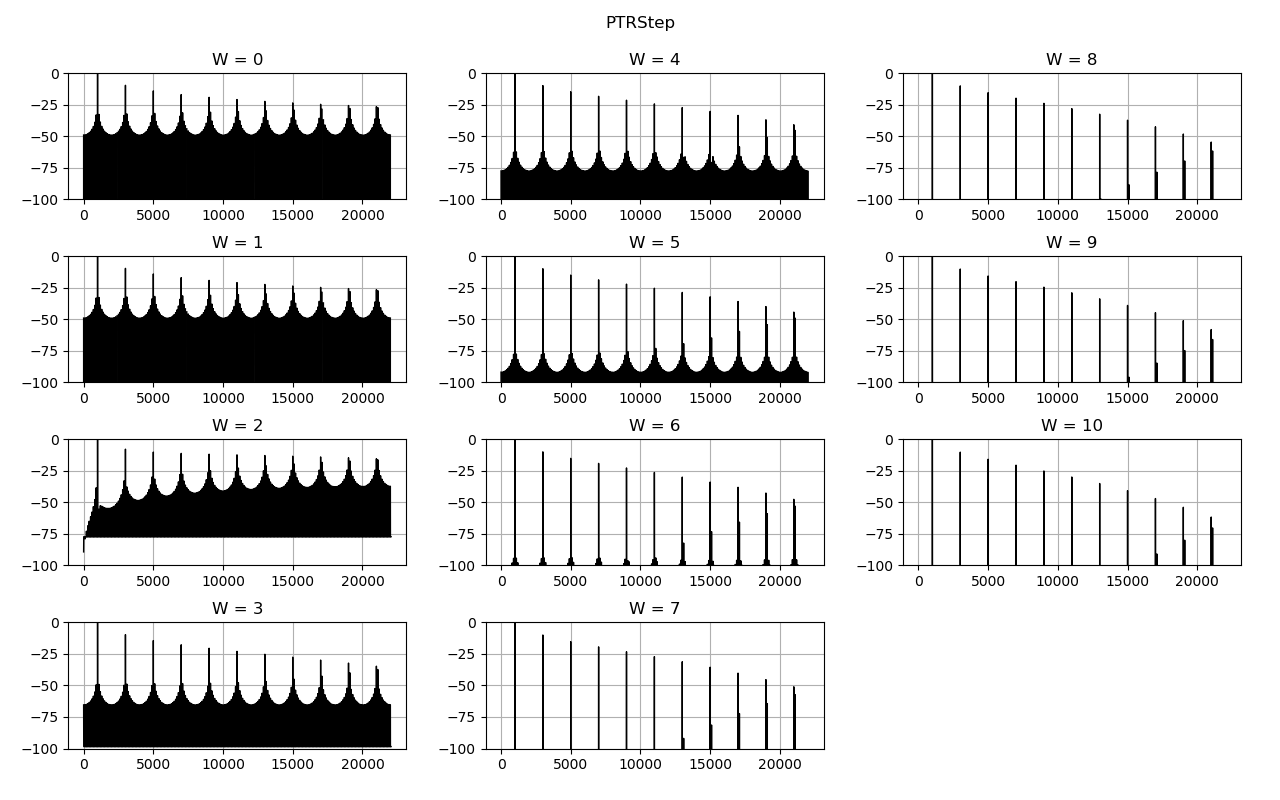
スペクトラムの比較です。横軸は周波数、縦軸はゲイン [dB] です。
1000 Hz でレンダリングした音です。
三角波、ランプ関数、ステップ関数のレンダリングのように、波形の 1 周期で \(M\) 個の PTR をつなぎ合わせると、周波数を高くしたときに 1 つの PTR の遷移領域を通り抜けないうちに次の区間に移動してしまうのでノイズが乗ります。ノイズが乗らずに出力できる周波数の上限は \(\dfrac{f_s}{MN}\) です。
鋸歯波の式はハードシンクを使わないときは \(h = 1\) を代入して式を簡略化できます。
鋸歯波のスケーリング係数 \(c(N)\) は PTR 論文の係数を使っています。 DPW 論文では鋸歯波について改良されたスケーリング係数 \(\hat{c}(N)\) が紹介されています。
\[ \hat{c}(N) = \frac{ \pi^{N-1} }{ N! \left(2 \sin \left(\pi f_0 T\right)\right)^{N-1} } \]
Maxima から得られた式と、式をフォーマットするコードへのリンクです。