PolyBLAMP Residual

Esqueda, Välimäki, Bilbao による ROUNDING CORNERS WITH BLAMP で紹介されている、 polyBLAMP residual を波形の角かどに足し合わせてエイリアシングを減らす方法を試します。

BLAMP Residual の導出

BLAMP は Band Limited rAMP function の略です。BLAMP は帯域制限されたインパルスを 2 回積分することで得られます。

帯域制限されたインパルス \(h(t)\) の式です。

\[ h(t) = f_s \mathrm{sinc} (f_s t) \]

\(h(t)\) を 1 回積分すると帯域制限されたステップ関数 (BLEP) の式になります。 BLEP は Band Limited stEP の略です。

\[ \begin{aligned} J h(t) &= \frac{1}{2} + \frac{1}{\pi}\mathrm{Si}(\pi f_s t)\\ \mathrm{Si}(x) &= \sum_{n=0}^{\infty} \frac{(-1)^n x^{2 n + 1}}{(2 n + 1)(2 n + 1)!} \end{aligned} \]

ここでは \(J\) で積分の演算を表しています。 \(\mathrm{Si}(x)\) は sine integral です。

\(J h(t)\) をもう一回積分すると BLAMP の式になります。

\[ J^2 h(t) = t \left( \frac{1}{2} + \frac{1}{\pi} \mathrm{Si}(\pi f_s t) \right) + \frac{\cos(\pi f_s t)}{\pi^2 f_s} \]

BLAMP の式からランプ関数 \(R(t)\) を引くと BLAMP residual が得られます。

\[ r(t) = J^2 h(t) - R(t) \]

• Ramp function - Wikipedia
• Heaviside step function - Wikipedia
• Dirac delta function - Wikipedia
• Trigonometric integral - Wikipedia

多項式による BLAMP residual の近似 (PolyBLAMP residual)

BLAMP residual を直接使うのは計算コストが高く実用的ではないそうです。そこで、計算コストを減らすために B-spline の基底関数を 2 回積分した式で BLAMP を近似する方法が提案されています。 B-spline の基底関数を 2 回積分した式は polyBLAMP と呼ばれています。

B-spline の定義です。

\[ \begin{aligned} N(i, 1, t) &= \begin{cases} 1, & \text{if}\enspace t_i \leq t < t_{i + 1},\\ 0, & \text{otherwise.} \end{cases}\\ N(i, k + 1, t) &= \frac{x - t_i}{t_{i + k} - t_i} N(i, k, t) + \frac{t_{i + k + 1} - t}{t_{i + k + 1} - t_{i + 1}} N(i + 1, k, t) \end{aligned} \]

\(N(i, k, t)\) を展開して得られる多項式の次数は \(k - 1\) となります。

すべての \(t_i\) をまとめたベクトル \(T\) のことをノットベクタといいます。

\[ T_k = (i_0, i_1, i_2, \dots, i_{3k - 4}, i_{3k - 3}, i_{3k - 2}) \]

ノットベクタのインデックス \(i\) の範囲は \([0, 3 k - 2]\) です。

ノットベクタの値の間隔が均等な B-spline のことをユニフォーム B-spline と呼びます。次の式は \(t\) の範囲を \(t_{k - 1} \leq t < t_k\) と仮定したときに、ユニフォーム B-spline の基底関数の導出に使えるノットベクタ \(\hat{T}_k\) です。

\[ \begin{aligned} \hat{T}_1 &= (-1, 0, 1, 2, 3)\\ \hat{T}_2 &= (-2, -1, 0, 1, 2, 3, 4, 5)\\ \hat{T}_3 &= (-3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7)\\ &\vdots \end{aligned} \]

\(\hat{T}_k\) を使い、 \(N(i, k, t)\) について \(i\) を \(0\) から \(k - 1\) まで増やしていくことで \(k\) 個の基底関数が得られます。

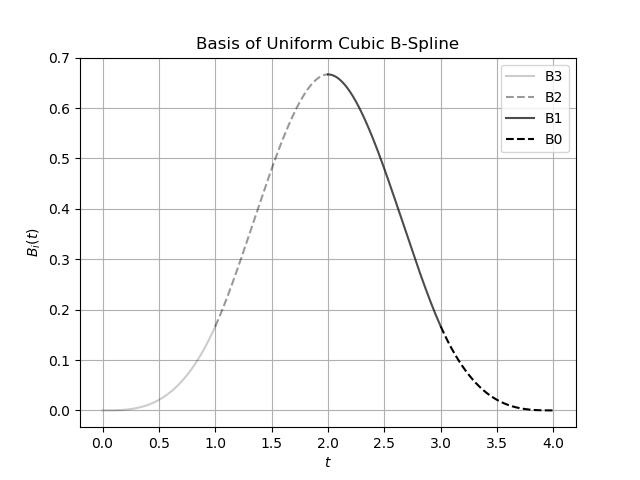
次の式は 3 次のユニフォーム B-spline の基底関数です。

\[ \begin{aligned} B_0(t) &= -\frac{t^3}{6} + \frac{t^2}{2} - \frac{t}{2} + \frac{1}{6}\\ B_1(t) &= \frac{t^3}{2} - t^2 + \frac{2}{3}\\ B_2(t) &= -\frac{t^3}{2} + \frac{t^2}{2} + \frac{t}{2} + \frac{1}{6}\\ B_3(t) &= \frac{t^3}{6} \end{aligned} \]

• Uniform Cubic B-Spline Curves

基底関数はつぎはぎになっています。まずは \(B_3(t)\) から始まり、 \(t\) を \(0\) から \(1\) に増やしていきます。 \(t\) が \(1\) を超えたら \(0\) に戻し、関数を \(B_2(t)\) に変えて、また \(t\) を \(0\) から \(1\) に増やしていきます。これを \(B_0(t)\) まで繰り返すことで基底関数が描画できます。

次のコードを実行すると使って基底関数を描画します。 Python3 のインタプリタにコピペすれば動きます。

import numpy
import matplotlib.pyplot as pyplot

def B0(t):
    return -t**3 / 6 + t**2 / 2 - t / 2 + 1 / 6

def B1(t):
    return t**3 / 2 - t**2 + 2 / 3

def B2(t):
    return -t**3 / 2 + t**2 / 2 + t / 2 + 1 / 6

def B3(t):
    return t**3 / 6

t = numpy.linspace(0, 1, 256)
y = numpy.hstack((B3(t), B2(t), B1(t), B0(t)))

pyplot.plot(y)
pyplot.show()

基底関数の見た目です。 \(B_i(t)\) がつぎはぎになっている様子が分かります。

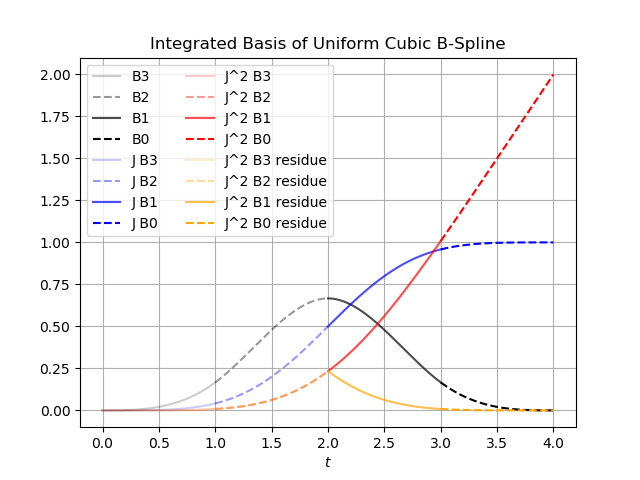
あとは 3 次のユニフォーム B-spline の基底関数を 2 回積分すれば 4点の polyBLAMP が得られます。 1 回目の積分を行います。

\[ \begin{aligned} J B_3(t) &= \frac{t^4}{24} + C_3\\ J B_2(t) &= -\frac{{{t}^{4}}}{8}+\frac{{{t}^{3}}}{6}+\frac{{{t}^{2}}}{4}+\frac{t}{6} + C_2\\ J B_1(t) &= \frac{{{t}^{4}}}{8}-\frac{{{t}^{3}}}{3}+\frac{2 t}{3} + C_1\\ J B_0(t) &= -\frac{{{t}^{4}}}{24}+\frac{{{t}^{3}}}{6}-\frac{{{t}^{2}}}{4}+\frac{t}{6} + C_0 \end{aligned} \]

積分定数を決めます。まず \(J B_3(0) = 0\) と仮定します。すると \(C_3 = 0\) となります。次に関数の間が滑らかにつながるようにしたいので \(J B_3(1) = J B_2(0)\) と仮定します。すると \(C_2 = J B_3(1)\) となります。あとは同様に \(J B_2(1) = J B_1(0)\) より \(C_1 = J B_2(1)\) 、 \(J B_1(1) = J B_0(0)\) より \(C_0 = J B_1(1)\) と積分定数が決まります。

\[ \begin{aligned} C_3 &= 0\\ C_2 &= J B_3(1) &&= \frac{1}{24}\\ C_1 &= J B_2(1) &&= \frac{1}{2}\\ C_0 &= J B_1(1) &&= \frac{23}{24}\\ \end{aligned} \]

積分定数が決まったので代入します。

\[ \begin{aligned} J B_3(t) &= \frac{t^4}{24}\\ J B_2(t) &= -\frac{{{t}^{4}}}{8}+\frac{{{t}^{3}}}{6}+\frac{{{t}^{2}}}{4}+\frac{t}{6} + \frac{1}{24}\\ J B_1(t) &= \frac{{{t}^{4}}}{8}-\frac{{{t}^{3}}}{3}+\frac{2 t}{3} + \frac{1}{2}\\ J B_0(t) &= -\frac{{{t}^{4}}}{24}+\frac{{{t}^{3}}}{6}-\frac{{{t}^{2}}}{4}+\frac{t}{6} + \frac{23}{24}\\ \end{aligned} \]

もう一回の積分も同じように積分定数を決めることができます。

\[ \begin{aligned} J^2 B_3(t) &= \frac{{{t}^{5}}}{120}\\ J^2 B_2(t) &= -\frac{{{t}^{5}}}{40}+\frac{{{t}^{4}}}{24}+\frac{{{t}^{3}}}{12}+\frac{{{t}^{2}}}{12}+\frac{t}{24}+J^2 B_3(1) &&= -\frac{{{t}^{5}}}{40}+\frac{{{t}^{4}}}{24}+\frac{{{t}^{3}}}{12}+\frac{{{t}^{2}}}{12}+\frac{t}{24}+\frac{1}{120}\\ J^2 B_1(t) &= \frac{{{t}^{5}}}{40}-\frac{{{t}^{4}}}{12}+\frac{{{t}^{2}}}{3}+\frac{t}{2}+J^2 B_2(1) &&= \frac{{{t}^{5}}}{40}-\frac{{{t}^{4}}}{12}+\frac{{{t}^{2}}}{3}+\frac{t}{2}+\frac{7}{30}\\ J^2 B_0(t) &= -\frac{{{t}^{5}}}{120}+\frac{{{t}^{4}}}{24}-\frac{{{t}^{3}}}{12}+\frac{{{t}^{2}}}{12}+\frac{23 t}{24}+J^2 B_1(1) &&= -\frac{{{t}^{5}}}{120}+\frac{{{t}^{4}}}{24}-\frac{{{t}^{3}}}{12}+\frac{{{t}^{2}}}{12}+\frac{23 t}{24}+\frac{121}{120}\\ \end{aligned} \]

2 回積分した式からランプ関数 \(R(x)\) を引くことで polyBLAMP residual が得られます。 3 次のときは \(x = 0\) が \(J^2 B_1(t)\) と \(J^2 B_2(t)\) の境界になるので、 \(J^2 B_1(t)\) と \(J^2 B_0(t)\) から \(t\) を引きます。 \(t\) を引いた式については積分定数を決め直します。

\[ \begin{aligned} J^2 \hat{B}_1(t) &= \frac{{{t}^{5}}}{40}-\frac{{{t}^{4}}}{12}+\frac{{{t}^{2}}}{3}+\frac{t}{2}+\frac{7}{30} - t &&= \frac{{{t}^{5}}}{40}-\frac{{{t}^{4}}}{12}+\frac{{{t}^{2}}}{3}-\frac{t}{2}+\frac{7}{30}\\ J^2 \hat{B}_0(t) &= -\frac{{{t}^{5}}}{120}+\frac{{{t}^{4}}}{24}-\frac{{{t}^{3}}}{12}+\frac{{{t}^{2}}}{12}+\frac{23 t}{24} - t + J^2 B_1(1) &&= -\frac{{{t}^{5}}}{120}+\frac{{{t}^{4}}}{24}-\frac{{{t}^{3}}}{12}+\frac{{{t}^{2}}}{12} - \frac{t}{24} - \frac{1}{120}\\ \end{aligned} \]

\(J^2 B_3(t)\) 、 \(J^2 B_2(t)\) 、 \(J^2 \hat{B}_0(t)\) 、 \(J^2 \hat{B}_1(t)\) が 4 point polyBLAMP residual の式です。

次の図は 3 次のユニフォーム B-spline の基底関数と、それを 1 回積分した関数、 2 回積分した関数、最終的に得られた 4 point polyBLAMP residual の見た目を表しています。

ここまでの式変形を Maxima のコードにしました。 wxMaxima にコピペすれば動きます。

N(i, k, t) :=
  if k = 1 then
    if concat('t, i) <= t and t < concat('t, i + 1) then 1 else 0
  else block([t_i: concat('t, i), t_ik: concat('t, i + k)],
    (t - t_i) / (concat('t, i + k - 1) - t_i) * N(i, k - 1, t)
    + (t_ik - t) / (t_ik - concat('t, i + 1)) * N(i + 1, k - 1, t)
  );

uniformBspline(k) := block(
  [
    result: [],
    T: makelist(concat('t, j) = j - k + 1, j, 0, 3 * k - 2)
  ],
  assume(concat('t, k - 1) <= t, t < concat('t, k)),
  for i: 0 thru 3 * k - 2 do assume(concat('t, i) < concat('t, i + 1)),
  for i: 0 thru k - 1 do
    result: endcons(expand(subst(T, N(i, k, t))), result),
  forget(concat('t, k - 1) <= t, t < concat('t, k)),
  result
);

findConstant(eq, residual) := block([result: [], J, C],
  J: integrate(last(eq), t),
  result: cons(J, result),
  C: subst(1, t, J),
  for i: length(eq) - 1 step -1 thru 1 do (
    J: integrate(eq[i], t) + C,
    if residual and i < length(eq) / 2 + 1 then J: J - t,
    result: cons(J, result),
    C: subst(1, t, J)
  ),
  result
);

eq: uniformBspline(4);      /* k - 1 が次数。 */
P: findConstant(eq, false); /* 1 回積分した式。 */
Q: findConstant(P, false);  /* 2 回積分した式。 */
R: findConstant(P, true);   /* polyBLAMP residual */

コードから得られた 6 point polyBLAMP residual の式です。

\[ \begin{aligned} J^2 B_{6, 0}(t) &= -\frac{{{t}^{7}}}{5040}+\frac{{{t}^{6}}}{720}-\frac{{{t}^{5}}}{240}+\frac{{{t}^{4}}}{144}-\frac{{{t}^{3}}}{144}+\frac{{{t}^{2}}}{240}-\frac{t}{720}+\frac{1}{5040}\\ J^2 B_{6, 1}(t) &= \frac{{{t}^{7}}}{1008}-\frac{{{t}^{6}}}{180}+\frac{{{t}^{5}}}{120}+\frac{{{t}^{4}}}{72}-\frac{5 {{t}^{3}}}{72}+\frac{13 {{t}^{2}}}{120}-\frac{29 t}{360}+\frac{61}{2520}\\ J^2 B_{6, 2}(t) &= -\frac{{{t}^{7}}}{504}+\frac{{{t}^{6}}}{120}-\frac{{{t}^{4}}}{24}+\frac{11 {{t}^{2}}}{40}-\frac{t}{2}+\frac{239}{840}\\ J^2 B_{6, 3}(t) &= \frac{{{t}^{7}}}{504}-\frac{{{t}^{6}}}{180}-\frac{{{t}^{5}}}{120}+\frac{{{t}^{4}}}{72}+\frac{5 {{t}^{3}}}{72}+\frac{13 {{t}^{2}}}{120}+\frac{29 t}{360}+\frac{61}{2520}\\ J^2 B_{6, 4}(t) &= -\frac{{{t}^{7}}}{1008}+\frac{{{t}^{6}}}{720}+\frac{{{t}^{5}}}{240}+\frac{{{t}^{4}}}{144}+\frac{{{t}^{3}}}{144}+\frac{{{t}^{2}}}{240}+\frac{t}{720}+\frac{1}{5040}\\ J^2 B_{6, 5}(t) &= \frac{{{t}^{7}}}{5040}\\ \end{aligned} \]

8 point polyBLAMP residual の式です。

\[ \begin{aligned} J^2 B_{8, 0}(t) &= -\frac{{{t}^{9}}}{362880}+\frac{{{t}^{8}}}{40320}-\frac{{{t}^{7}}}{10080}+\frac{{{t}^{6}}}{4320}-\frac{{{t}^{5}}}{2880}+\frac{{{t}^{4}}}{2880}-\frac{{{t}^{3}}}{4320}+\frac{{{t}^{2}}}{10080}-\frac{t}{40320}+\frac{1}{362880}\\ J^2 B_{8, 1}(t) &= \frac{{{t}^{9}}}{51840}-\frac{{{t}^{8}}}{6720}+\frac{{{t}^{7}}}{2520}-\frac{{{t}^{5}}}{360}+\frac{{{t}^{4}}}{120}-\frac{7 {{t}^{3}}}{540}+\frac{{{t}^{2}}}{84}-\frac{31 t}{5040}+\frac{1}{720}\\ J^2 B_{8, 2}(t) &= -\frac{{{t}^{9}}}{17280}+\frac{{{t}^{8}}}{2688}-\frac{{{t}^{7}}}{2016}-\frac{{{t}^{6}}}{480}+\frac{19 {{t}^{5}}}{2880}+\frac{{{t}^{4}}}{192}-\frac{49 {{t}^{3}}}{864}+\frac{397 {{t}^{2}}}{3360}-\frac{4541 t}{40320}+\frac{347}{8064}\\ J^2 B_{8, 3}(t) &= \frac{{{t}^{9}}}{10368}-\frac{{{t}^{8}}}{2016}+\frac{{{t}^{6}}}{270}-\frac{{{t}^{4}}}{36}+\frac{151 {{t}^{2}}}{630}-\frac{t}{2}+\frac{1487}{4536}\\ J^2 B_{8, 4}(t) &= -\frac{{{t}^{9}}}{10368}+\frac{{{t}^{8}}}{2688}+\frac{{{t}^{7}}}{2016}-\frac{{{t}^{6}}}{480}-\frac{19 {{t}^{5}}}{2880}+\frac{{{t}^{4}}}{192}+\frac{49 {{t}^{3}}}{864}+\frac{397 {{t}^{2}}}{3360}+\frac{4541 t}{40320}+\frac{347}{8064}\\ J^2 B_{8, 5}(t) &= \frac{{{t}^{9}}}{17280}-\frac{{{t}^{8}}}{6720}-\frac{{{t}^{7}}}{2520}+\frac{{{t}^{5}}}{360}+\frac{{{t}^{4}}}{120}+\frac{7 {{t}^{3}}}{540}+\frac{{{t}^{2}}}{84}+\frac{31 t}{5040}+\frac{1}{720}\\ J^2 B_{8, 6}(t) &= -\frac{{{t}^{9}}}{51840}+\frac{{{t}^{8}}}{40320}+\frac{{{t}^{7}}}{10080}+\frac{{{t}^{6}}}{4320}+\frac{{{t}^{5}}}{2880}+\frac{{{t}^{4}}}{2880}+\frac{{{t}^{3}}}{4320}+\frac{{{t}^{2}}}{10080}+\frac{t}{40320}+\frac{1}{362880}\\ J^2 B_{8, 7}(t) &= \frac{{{t}^{9}}}{362880} \end{aligned} \]

三角波オシレータへの応用

4 point polyBLAMP residual を素朴な三角波オシレータの角かどに足し合わせてエイリアシングノイズを低減します。

素朴な三角波は次の式で生成できます。

\[ \mathrm{Tri}(n) = 4 \left| \frac{n f_0}{f_s} - \frac{1}{2} \right| - 1 \]

\(n\) は経過したサンプル数、 \(f_0\) はオシレータの周波数、 \(f_s\) はサンプリング周波数です。

絶対値を外したときの \(n\) の係数がランプ関数の傾き \(\mu\) になります。

\[ \mu = \frac{4 f_0}{f_s} \]

三角波では次の図のように波形の 1 周期の内にランプ関数の角が 4 つ現れます。

角が現れるのは正規化された位相 \(\phi = \dfrac{n f_0}{f_s} \bmod 1\) が \(0\) か \(0.5\) のときです。角の位置 \(d\) は \(\phi\) から計算できます。

\[ d = \begin{cases} \dfrac{\phi f_s}{f_0}, &\quad \text{if}\enspace 0 \leq \phi < \frac{f_0}{f_s}\\\\ \dfrac{(\phi - 0.5) f_s}{f_0}, &\quad \text{if}\enspace 0.5 \leq \phi < 0.5 + \frac{f_0}{f_s}\\ \end{cases} \]

ランプ関数の向きが \(x \leq 0\) のときに \(\pm x\) となる場合は \(1 - d\) とします。

実装例です。この Python3 + NumPy の実装はかなり遅いです。完全なコードは長いのでリンクにしました。

• コードを読む (github.com)

def blamp_residual4(d):
    return (
        d**5 / 120,
        -d**5 / 40 + d**4 / 24 + d**3 / 12 + d**2 / 12 + d / 24 + 1 / 120,
        d**5 / 40 - d**4 / 12 + d**2 / 3 - d / 2 + 7 / 30,
        -d**5 / 120 + d**4 / 24 - d**3 / 12 + d**2 / 12 - d / 24 + 1 / 120,
    )

class TriangleBLAMP:
    def __init__(self, points, samplerate, frequency, residual_func):
        self.residual_func = residual_func

        self.s = numpy.zeros(points)
        self.isEdge = numpy.zeros(points)

        self.edgePoint = points // 2 - 1

        self.phase = 0
        self.tick = frequency / samplerate
        self.mu = 4 * frequency / samplerate
        self.d = 0

    def process(self):
        self.s[-1] = 4 * numpy.abs(self.phase - 0.5) - 1

        if self.isEdge[self.edgePoint] == 1:
            self.s += self.mu * (
                self.residual_func(self.d) + numpy.flip(self.residual_func(1 - self.d)))
        elif self.isEdge[self.edgePoint] == -1:
            self.s -= self.mu * (
                self.residual_func(self.d) + numpy.flip(self.residual_func(1 - self.d)))

        self.phase += self.tick
        if self.phase >= 0.5 and self.phase < 0.5 + self.tick:
            self.isEdge[-1] = 1
            self.d = (self.phase - 0.5) / self.tick
        elif self.phase > 1.0:
            self.phase -= 1.0
            self.isEdge[-1] = -1
            self.d = self.phase / self.tick
        else:
            self.isEdge[-1] = 0

        self.s = numpy.roll(self.s, -1)
        self.isEdge = numpy.roll(self.isEdge, -1)
        return self.s[0]

def render_blamp(points, samplerate, frequency, residual_func):
    """ 1 秒分の波形をレンダリング。 """
    triangle = TriangleBLAMP(points, samplerate, frequency, residual_func)
    data = numpy.empty(n_sample)
    for _ in range(points - 2):
        triangle.process()
    for i in range(len(data)):
        data[i] = triangle.process()
    return data

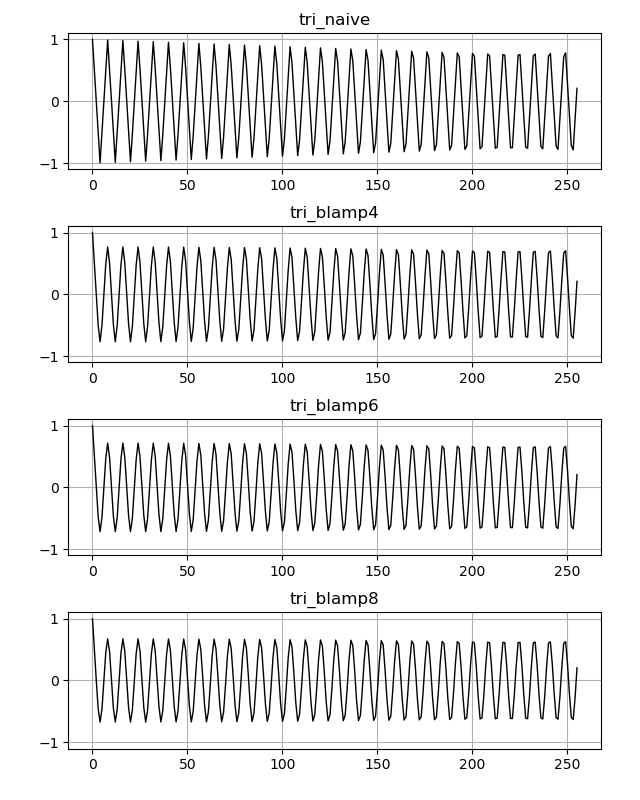
tri_blamp4 = render_blamp(4, samplerate, frequency, blamp_residual4)

\(f_s = 44100, f_0 = 5500\) としてレンダリングした三角波の音です。

波形です。 polyBLAMP residual を足し合わせた波形は角が丸まったように見えます。

周波数成分の比較です。 polyBLAMP residual の点数が増えるとノイズが減っていることが分かります。

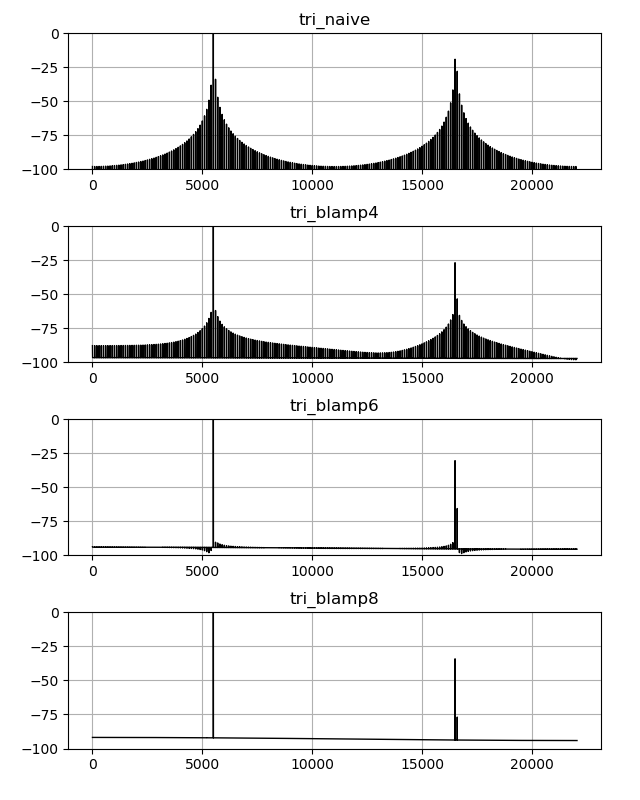
三角波では polyBLAMP residual が \(k\) 点のとき \(f_s / k\) Hz までならノイズ低減が見込めます。 \(f_s / k\) Hz を超えると residual を足し合わせている領域がランプ関数だという仮定が崩れるので逆にノイズが増えます。

\(f_s = 44100\) のときに使える最も高い周波数です。

• \(k = 4 \to\) 11025 Hz
• \(k = 6 \to\) 7350 Hz
• \(k = 8 \to\) 5512.5 Hz

次の図は仮定が崩れるパターンを示しています。

ハードクリップへの応用の検討

論文ではハードクリップへの応用についても触れられているので試します。

ハードクリップとは波形に clamp 関数をかける処理のことです。 clamp 関数は次のように定義できます。

def clamp(value, low, high):
    if value < low:
        return low
    elif value > high:
        return high
    return value

PolyBLAMP residual をハードクリップに適用するためには、入力信号からランプ関数の角かどの位置 \(d\) と、傾き \(\mu\) を推定する必要があります。

波形の角の部分だけを取り出した図です。 4 point polyBLAMP residual は角がインデックス 1 と 2 の間にあると仮定しています。

論文では \(d\) と \(\mu\) の推定にラグランジュ補間を使っています。次の式は 4 つのサンプルを通過するラグランジュ補間の多項式です。

\[ \begin{aligned} a &= -\frac{1}{6} s[0] + \frac{1}{2} s[1] - \frac{1}{2} s[2] + \frac{1}{6} s[3]\\ b &= s[0] -\frac{5}{2} s[1] + 2 s[2] - \frac{1}{2} s[3]\\ c &= -\frac{6}{11} s[0] + 3 s[1] - \frac{3}{2} s[2] + \frac{1}{3} s[3]\\ d &= s[0] \end{aligned} \]

ニュートン法で、次の方程式を \(D = 1 + d\) について解きます。

\[ a D^3 + b D^2 + c D + e - \rho = 0 \]

方程式をニュートン法の漸化式にします。

\[ \begin{aligned} D_0 &= 1.5\\ D_{q + 1} &= D_q - \frac{f(D_q)}{f'(D_q)}\\ &= D_q - \frac{a D_q^3 + b D_q^2 + c D_q + e - \rho}{3 a D_q^2 + 2 b D_q + c}\\ d &= D - 1\\ \mu &= f'(D_Q) \end{aligned} \]

\(\rho\) は角の高さです。例えば全波整流では \(0\) 、音量 \(L\) でのハードクリッピングでは \(\pm L\) となります。 \(D_Q\) はニュートン法から得られた最終的な値です。

実装の詳細としてランプ関数の向きによる分岐があります。ランプ関数の向きは、 \(x\) の符号と、 0 以上なのか 0 以下なのかの条件の組み合わせで、合計 4 つあります。

テストします。次のコードではランプ関数が \(x > 0\) のときに \(x\) となる場合だけを扱っています。

import numpy

def f(D, a, b, c, e, rho):
    return a * D**3 + b * D**2 + c * D + e - rho

def f_dash(D, a, b, c):
    return 3 * a * D**2 + 2 * b * D + c

def lagrange4(s0, s1, s2, s3):
    return (
        -1 / 6 * s0 + 1 / 2 * s1 - 1 / 2 * s2 + 1 / 6 * s3,
        s0 - 5 / 2 * s1 + 2 * s2 - 1 / 2 * s3,
        -6 / 11 * s0 + 3 * s1 - 3 / 2 * s2 + 1 / 3 * s3,
        s0,
    )

def estimate(sign, rho, s0, s1, s2, s3):
    a, b, c, e = lagrange4(s0, s1, s2, s3)
    D = 1.5
    for _ in range(128):  # 実験なので多めに回す。
        D = D - f(D, a, b, c, e, rho) / f_dash(D, a, b, c)
    return (
        D,
        f(D, a, b, c, e, rho),
        numpy.abs(f_dash(D, a, b, c)),
    )

def blamp_residual(d, slope):
    return (
        slope * (-d**5 / 120 + d**4 / 24 - d**3 / 12 + d**2 / 12 - d / 24 + 1 / 120),
        slope * (d**5 / 40 - d**4 / 12 + d**2 / 3 - d / 2 + 7 / 30),
        slope * (-d**5 / 40 + d**4 / 24 + d**3 / 12 + d**2 / 12 + d / 24 + 1 / 120),
        slope * (d**5 / 120),
    )

def ramp(x, scale):
    return scale * numpy.maximum(0, x)

rho = 1.0
scale = 1
sign = 1  # ランプ関数の x の符号。
x = numpy.arange(4, dtype=numpy.float64)
sig = ramp(x - 1.25, scale) + rho

D, Dy, slope = estimate(sign, rho, *sig)
result = sig + polyblamp_residual(D - 1, slope)

# プロットは省略。

推定結果の図です。ラグランジュ補間がうまくできていません。

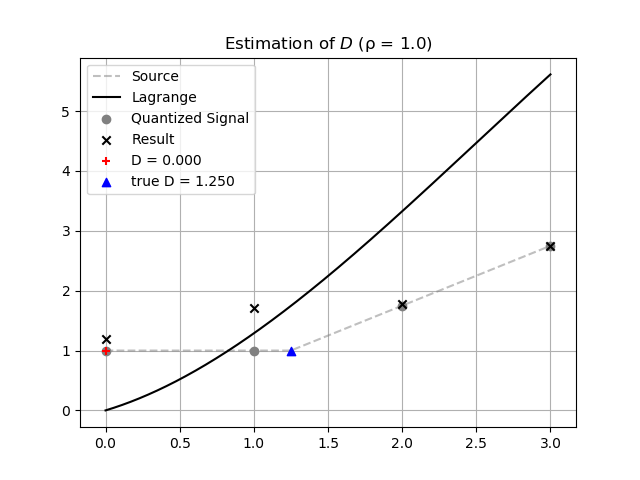
論文の式はラグランジュ補間での \(\rho\) の使い方が間違っているように思います。コードの estimate を修正します。

def estimate(sign, rho, s0, s1, s2, s3):
    a, b, c, e = lagrange4(s0 - rho, s1 - rho, s2 - rho, s3 - rho)
    D = 1.5
    for _ in range(128):
        D = D - f(D, a, b, c, e, 0) / f_dash(D, a, b, c)
    return (
        D,
        f(D, a, b, c, e, 0),
        numpy.abs(f_dash(D, a, b, c)),
    )

修正した結果です。補間はうまく動きましたが、値の推定は間違っています。

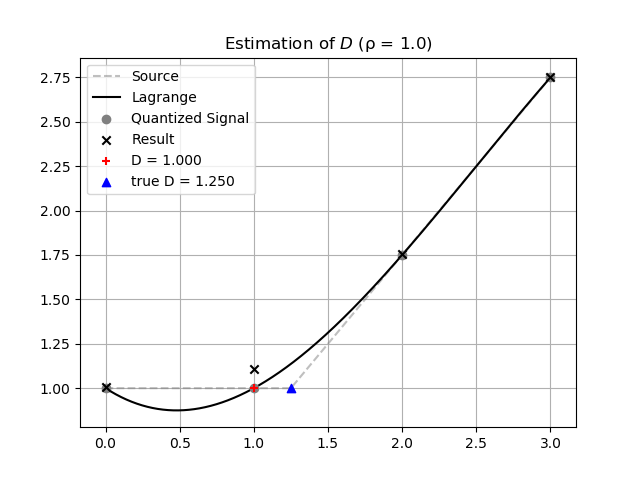
さらに、実データでは 3.0 の位置にあるサンプルがランプ関数に従わないケースも考えられます。次の図は \(\rho = -0.3\) で、入力信号が [-0.300, -0.300, -0.001, -0.150] のときの推定結果です。

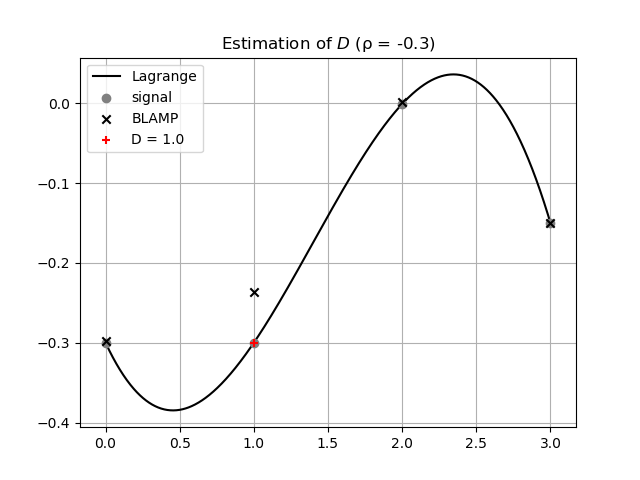
ラグランジュ補間の振る舞いを考えると、論文の手法では常に D = 1.0 と推定されてしまうような気がします。別の推定方法を使うにしても、入力信号がランプ関数に従わないケースがありえることから、何らかの追加情報がなければ角の位置の推定は困難に思えます。

とりあえず実装してみました。

• ハードクリップの実装を見る (github.com)

音のサンプルです。

角の位置 \(d\) は 3 番目の信号 \(s_3\) から 2 番目の信号 \(s_2\) を引いた値を傾きとして、 \(d = \dfrac{s_2 - \rho}{|s_3 - s_2|}\) で求めています。入力信号がランプ関数に従わないケースは無視しています。

この実装は clamp だけをつかった素朴な実装よりノイズが増えます。歪み系エフェクトの部品としては使えるかもしれません。

参考文献

• Fabián Esqueda, Vesa Välimäki, and Stefan Bilbao. “Rounding corners with BLAMP.” Proc. Int. Conf. Digital Audio Effects (DAFx-16), Brno, Czech Republic. 2016.
• Vesa Välimäki, Jussi Pekonen, and Juhan Nam. “Perceptually informed synthesis of bandlimited classical waveforms using integrated polynomial interpolation.” The Journal of the Acoustical Society of America 131.1 (2012): 974-986.
• Uniform Cubic B-Spline Curves
• 1.4 B-spline curves and surfaces
• Ramp function - Wikipedia
• Heaviside step function - Wikipedia
• Dirac delta function - Wikipedia
• Trigonometric integral - Wikipedia