gibbs

この文章で実装したコードを GitHub で見ることができます。実行するには SciPy と matplotlib が必要です。パラメータを変えて遊んでみてください。

Gottleib と Shu の論文で先行研究として紹介されていた方法です。ここではFIRフィルタとして実装します。

import numpy
import matplotlib.pyplot as pyplot
from scipy.special import eval_gegenbauer, gamma


def spectralLowpass(sig, numSeries):
    if numSeries >= len(sig):
        return sig
    spec = numpy.fft.rfft(sig)
    spec[numSeries + 1 : len(sig) - 1] = 0
    return numpy.fft.irfft(spec)


def additiveSaw(length, numSeries):
    return spectralLowpass(numpy.linspace(-1, 1, length), numSeries)


def applyFilter(source, filterFunc, numSeries, power=1):
    spec = numpy.fft.rfft(source)
    filt = numpy.zeros(len(spec))
    m = numSeries + 1
    for i in range(m):
        eta = i / m
        filt[i] = filterFunc(eta) ** power

    applied = numpy.fft.irfft(spec * filt)
    filt = numpy.append(filt[m:0:-1], filt[: m + 1])  # プロットに使用。

    return (applied, filt)


def plotGibbsSuppression(length, filterFunc, numSeries=16, power=1):
    source = additiveSaw(length, numSeries)
    suppressed, filt = applyFilter(source, filterFunc, numSeries, power)
    # 結果をプロットする。ここでは省略。

フィルタの適用は plotGibbsSuppression から行います。 power の値を大きくするとフィルタのカットオフ周波数が高くなります。入力信号は低いほうから numSeries 個の周波数成分を持つ鋸歯波です。

# Lanczosフィルタの適用例。
plotGibbsSuppression(1024, lanczos, 16, 1)

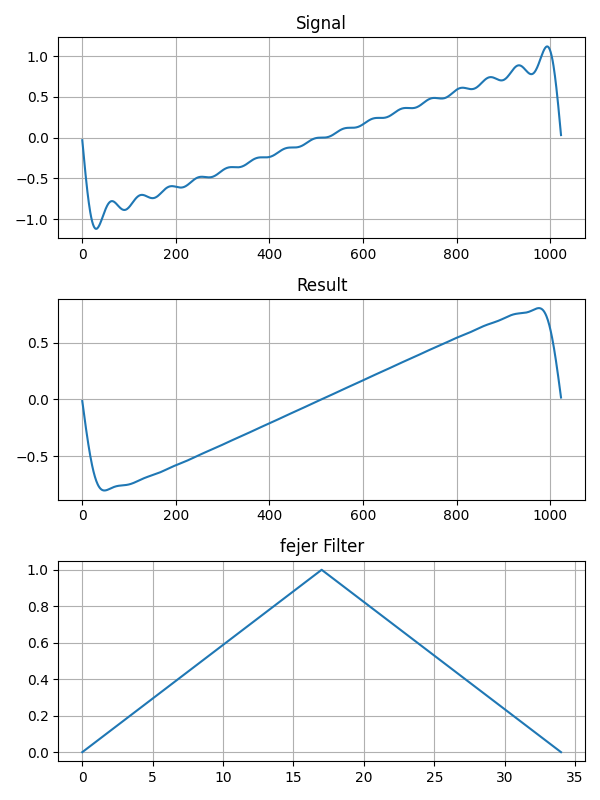
def fejer(eta):
    return 1 - eta

フィルタを適用した結果です。画像の Signal は入力信号、 Result はフィルタを適用した結果です。一番下の図は FIR フィルタの係数です。

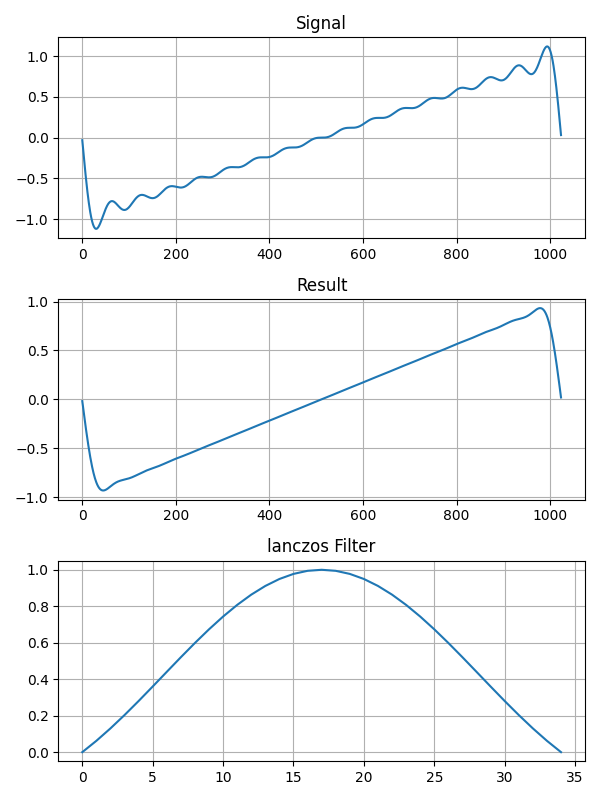
def lanczos(eta):
    return numpy.sinc(eta)

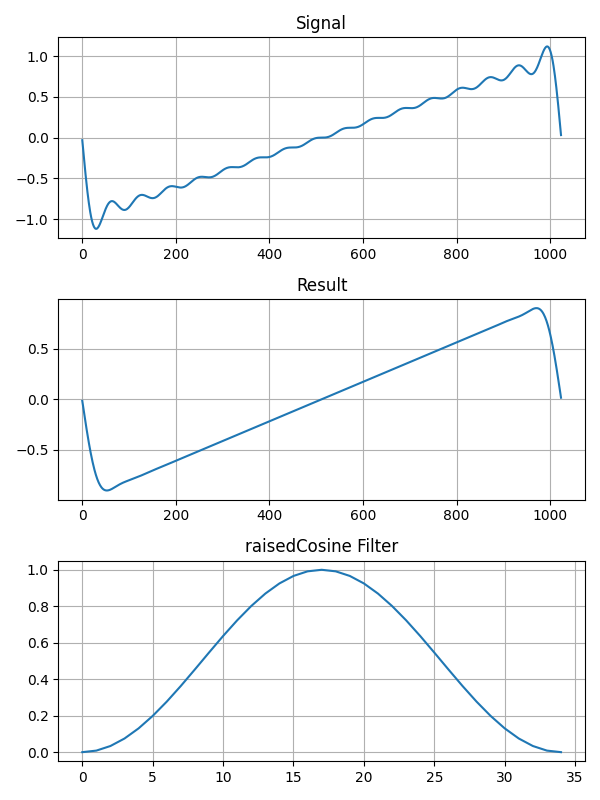
def raisedCosine(eta):
    return (1 + numpy.cos(numpy.pi * eta)) / 2

\[ \sigma_4(\eta) = \sigma_3^4(\eta)(35 - 84\sigma_3(\eta) + 70\sigma_3^2(\eta) - 20\sigma_3^3(\eta)) \]

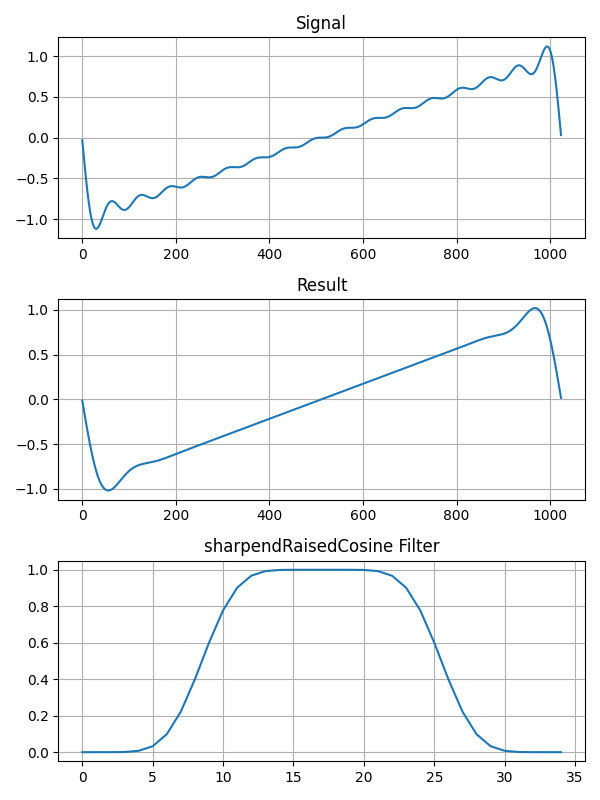
def sharpendRaisedCosine(eta):
    s = raisedCosine(eta)
    return s**4 * (35 - 84 * s + 70 * s**2 - 20 * s**3)

def exponential(eta, alpha=8, p=4):
    return numpy.exp(-alpha * eta**p)

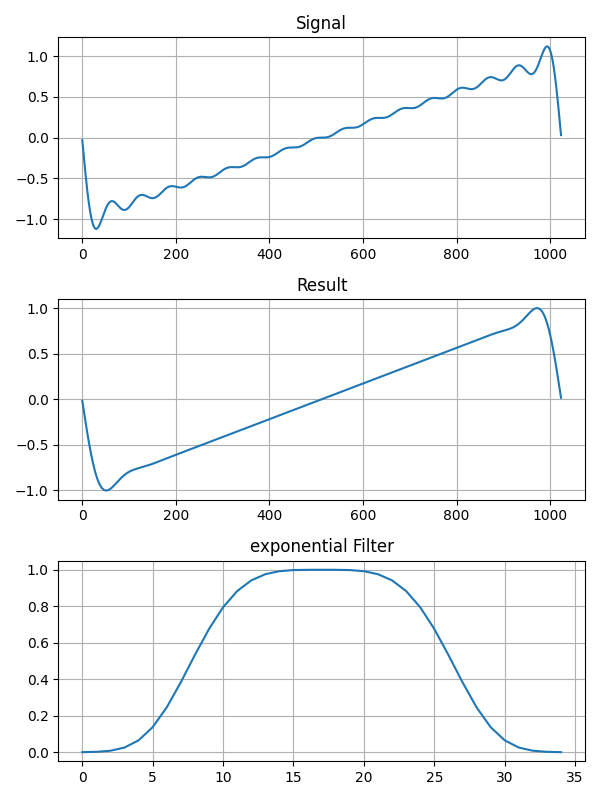
\[ \sigma_6(\eta) = 1 - \frac{(2p-1)!}{(p-1)!^2} \int_0^{\eta} [t(1-t)]^{p-1} dt \]

declare(eta, real, t, real);
p: 4;
I: integrate((t*(1 - t))**(4 - 1), t, 0, eta);
expand(1 - (2 * p - 1)! / (p - 1)!**2 * I);

def daubechies4(eta):
    return 1 - 35 * eta**4 + 84 * eta**5 - 70 * eta**6 + 20 * eta**7

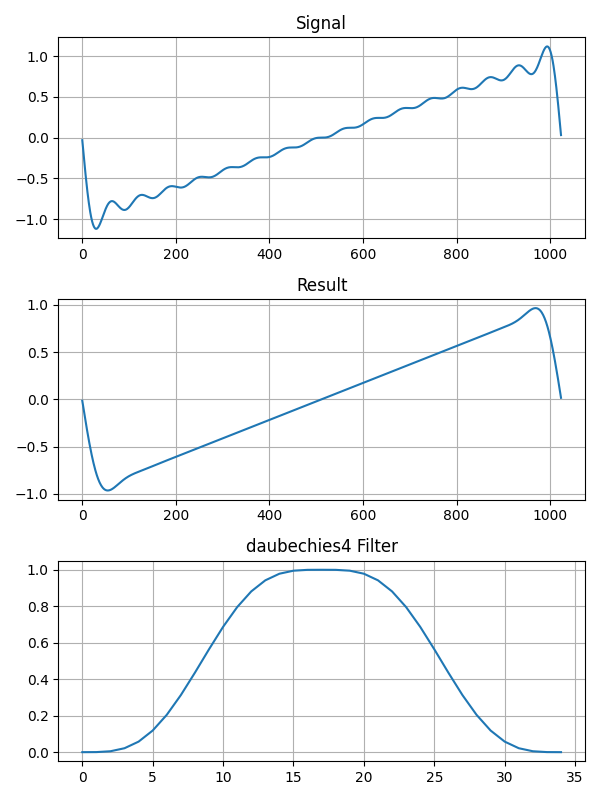
Gottleib と Shu の論文で提案されていた方法です。この方法はギブス現象が発生する前の信号が解析的な形で表現できるときに使えます。ここでの解析的な形とは \(f(x) = a_0 + a_1 x + a_2 x^2 + a_3 x^3 + \dots\) というような形、つまり多項式のことです。

\[ \begin{aligned} \hat{g}_k^{\lambda} &= \frac{1}{h_k^{\lambda}} \int_{-1}^{1} (1 - x^2)^{\lambda - \frac{1}{2}}f_N(x)C_k^{\lambda}(x)\,dx, \\ h_k^{\lambda} &= \pi^{\frac{1}{2}}C_k^{\lambda}(x) \frac{\Gamma(\lambda + \frac{1}{2})}{\Gamma(\lambda)(k + \lambda)}, \\ 0 &\le k \le m. \end{aligned} \]

Gegenbauer 係数 \(\hat{g}_k^{\lambda}\) を用いて出力信号 \(g^m(x)\) を合成します。

\(g^m(x)\) は真の信号と比例関係にあるそうです。つまり出力信号の振幅を調整する必要があります。

def gottliebShu(sig, N, L=0.25):
    """
    :param sig: numpy.array input signal.
    :param N: Number of spectral partial sum or number of overtone.
    :param L: Positive real constant.
    """
    lam = L * N  # N が大きいと eval_gegenbauerでオーバーフローする。

    x = numpy.linspace(-1.0, 1.0, len(sig))
    k = numpy.arange(0, int(N / 2))
    ggnbr = eval_gegenbauer(numpy.tile(numpy.vstack(k), len(sig)), lam, x)
    ggnbr_t = numpy.transpose(ggnbr)

    h_k_lam = (
        numpy.sqrt(numpy.pi) * ggnbr_t[-1] * gamma(lam + 0.5) / gamma(lam) / (k + lam)
    )

    g_hat = (
        numpy.sum(numpy.power(1 - x * x, numpy.abs(lam - 0.5)) * sig * ggnbr, axis=1)
        / h_k_lam
    )

    return (numpy.sum(g_hat * ggnbr_t, axis=1), g_hat)

適用した結果です。画像の一番下の図は \(\hat{g}_k^{\lambda}\) です。

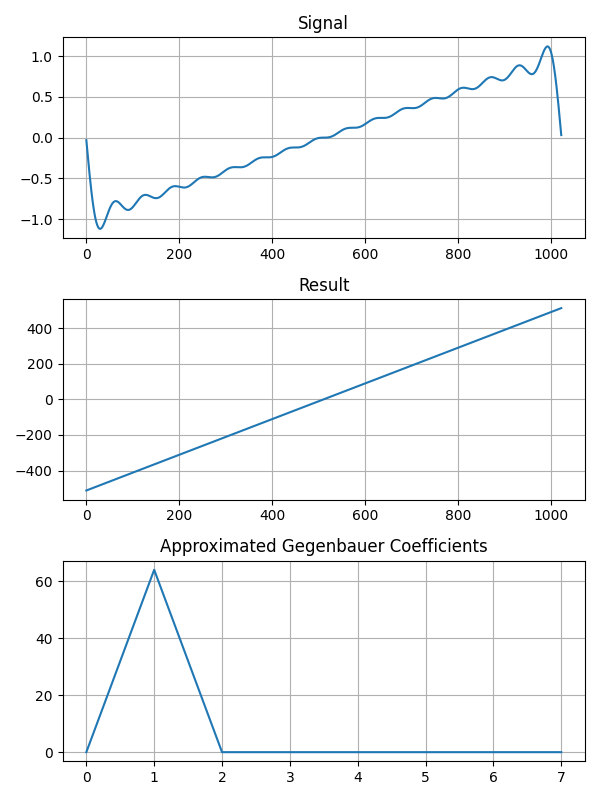
\(C_1^{\lambda}\) の成分で完璧に再現できています。 \(C_1^{\lambda}\) の成分は \(y = ax\) の形の直線です。入力信号の鋸歯波も直線なので、これはどうやっても成功しそうです。

def additiveNoise(length, numSeries):
    return spectralLowpass(numpy.random.uniform(-1, 1, length), numSeries)


def analyticSignal(length, numSeries):
    sig = numpy.linspace(-1, 1, length)
    noise = numpy.zeros(length)
    order = 128
    rand = numpy.random.random(order)
    for i in range(order):
        noise += rand[i] * sig**(i + 1)
    return spectralLowpass(noise, numSeries)


def plotGottleibShuNoise(length, signalFunc, numSeries=16):
    source = signalFunc(length, numSeries)
    suppressed, g_hat = gottliebShu(source, numSeries)
    regibbsed = spectralLowpass(suppressed, numSeries)
    # 結果をプロットする。ここでは省略。


plotGottleibShuNoise(1024, additiveNoise, 16)
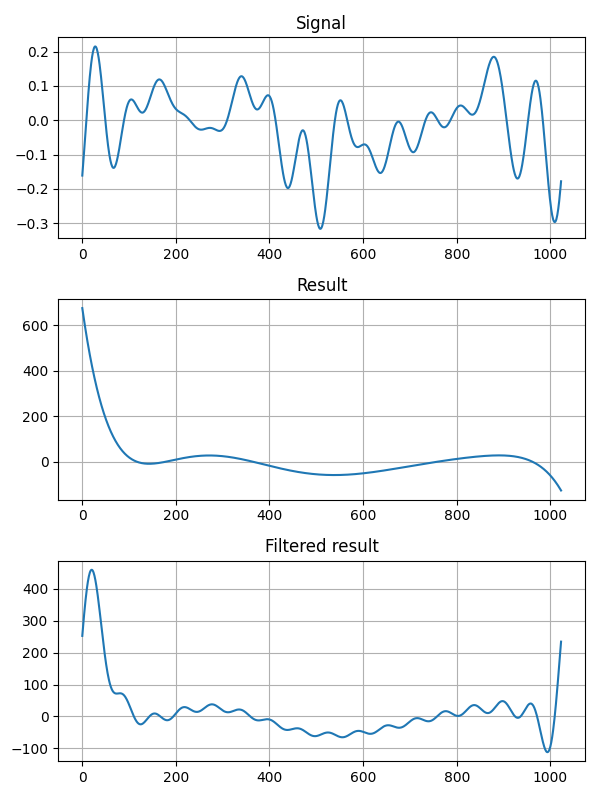
plotGottleibShuNoise(1024, analyticSignal, 16)

以下は additiveNoise の結果です。 additiveNoise は乱数で生成したノイズにローパスフィルタをかけた信号です。画像の Filtered result はギブス現象を抑えた結果にフィルタをかけて、周波数成分の数を入力信号と揃えた信号です。

additiveNoise について入力信号と、ギブス現象を抑えた結果にフィルタをかけた信号の周波数の比較です。 power は周波数成分の大きさ、 phase は周波数成分の位相です。

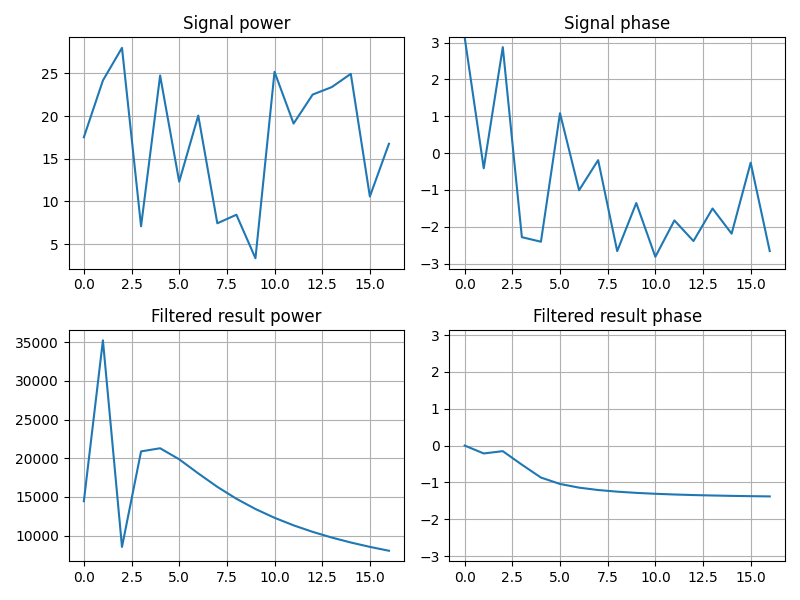
additiveNoise ではギブス現象の抑制に失敗しています。乱数で生成したノイズは不連続点を含むので Gegenbauer Polynomial を使う方法をそのまま使うことはできません。

以下は analyticSignal の結果です。 analyticSignal は解析的な要素のみで合成した信号です。

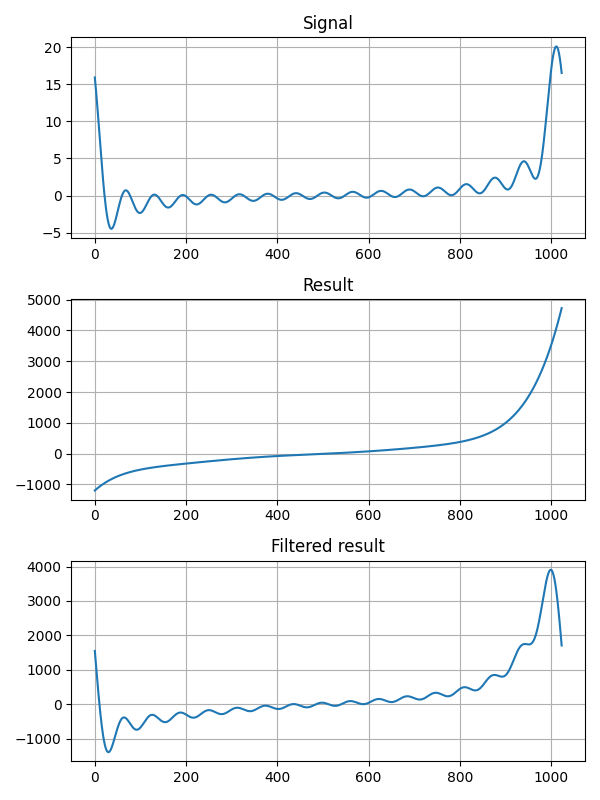
analyticSignal について入力信号と、ギブス現象を抑えた結果にフィルタをかけた信号の周波数の比較です。

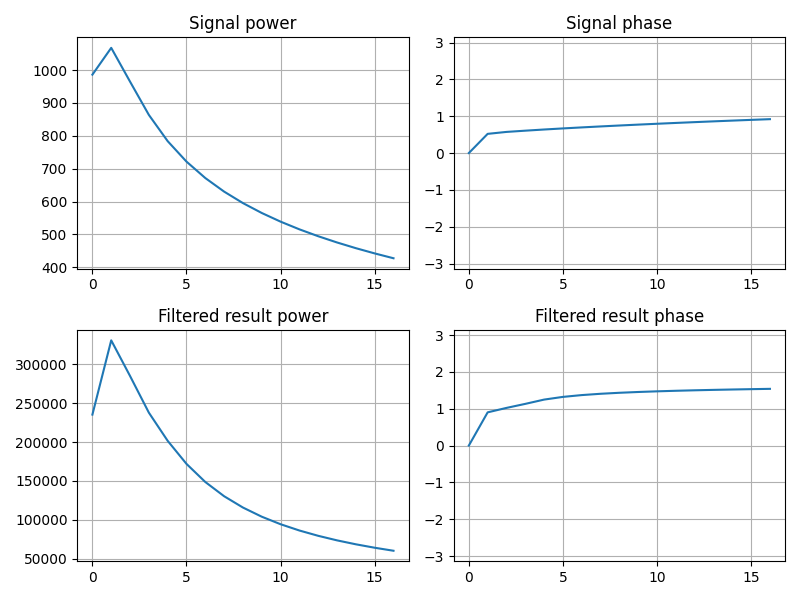
analyticSignal では理論どおりにギブス現象の抑制に成功していると言えそうです。ただし今回選んだパラメータでは目に見える誤差が出ています。 \(m\) の値を大きくすれば誤差を減らすことができます。

\(\hat{g}_k^{\lambda}\) を求める式の中にある \(f_N(x)\) は \([-1, 1]\) の区間で連続であることが求められています。つまり、この方法を現実の信号に適用するには不連続点を見つけて、連続な区間ごとに信号を分割する必要があります。

\(\lambda\) と \(m\) が大きいと Gegenbauer Polynomial の計算でオーバーフローすることがあります。これが問題になるときは任意精度で実装するしかなさそうです。

Gegenbauer polynomial を使う方法の \(m\) を増やしていくことで、 Gegenbauer polynomial による信号の加算合成ができます。ただし信号の両端の値が非常に大きくなるので Tukey 窓などを掛け合わせて抑える必要があります。また \(\lambda = 1\) とすることで、ある程度はオーバーフローを避けることができます。