exppoly_envelope

何かあれば GitHub のリポジトリに issue を作るか ryukau@gmail.com までお気軽にどうぞ。

Update: 2025-01-07

Table of Contents

WobblingMetalBoard を作っているときに次のエンベロープを思いつきました。

$E (t) = t^{α} e^{- β t}$

$t$ は時間、 $α, β$ は任意の定数です。簡単に性質を調べて実装します。

$E (t)$ を $t$ について微分します。 Maxima を使います。

env(t) := t^α * exp(-β * t);
env_d1: diff(env(t), t);
env_d2: diff(env_d1, t);

$\begin{aligned} \dot{E} (t) & = (- β t^{α} + α t^{α - 1}) e^{- β t} \\ \ddot{E} (t) & = (β^{2} t^{α} - 2 α β t^{α - 1} + (α - 1) α t^{α - 2}) e^{- β t} \end{aligned}$

$\dot{E} (t)$ の傾きが 0 になるときの $t$ を求めます。

solve(env_d1 = 0, t);

次の解が得られました。

$t = \frac{α}{β}$

実際に計算してみると $t = \frac{α}{β}$ のとき $E (t)$ が最大となります。つまりアタックの長さは $\frac{α}{β}$ です。

アタックの長さから振幅を $[0, 1]$ に正規化した $\hat{E} (t)$ を求めることができます。

$\hat{E} (t) = \frac{E (t)}{E (\frac{α}{β})}$

NumPy を使った実装例です。

import numpy

def expPoly(α, β, time):
    return time**α * numpy.exp(-β * time)

def expPolyNormalized(α, β, time):
    normalize = expPoly(α, β, α / β)
    return time**α * numpy.exp(-β * time) / normalize

time = numpy.linspace(0, 16, 1024)
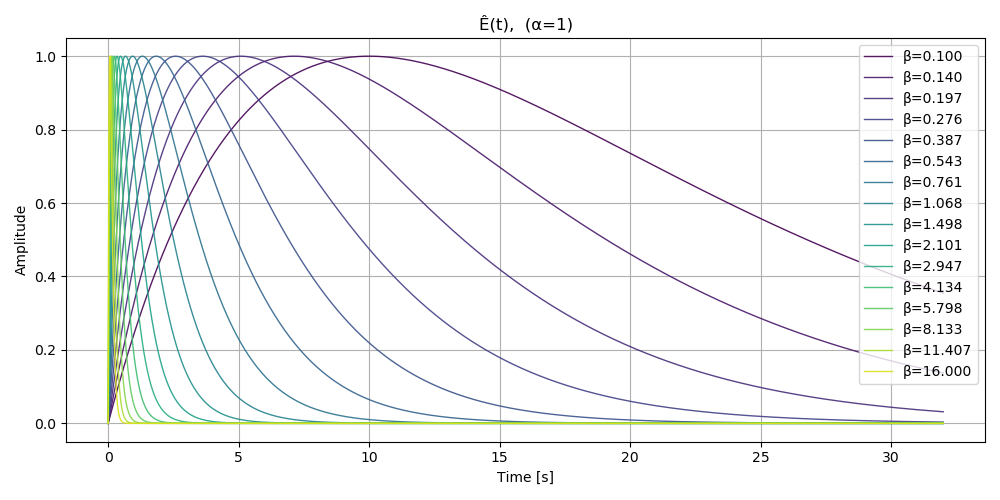
envelope = expPolyNormalized(1, 1, time)

$β = 1$ に固定して $α$ を変えたときの $\hat{E} (t)$ のプロットです。

Image of poly-exp envelope with varying alpha.

$α = 1$ に固定して $β$ を変えたときの $\hat{E} (t)$ のプロットです。

Image of poly-exp envelope with varying beta.

$E (t)$ は $t$ が $+ \infty$ に到達すると $0$ になります。適当に計算を打ち切るために $\hat{E} (t) = x$ となる時間 $t$ を求めます。 $x = \frac{t^{α} e^{- β t}}{E (\frac{α}{β})}$ を $t$ について解いてみます。この問題は Maxima では解けなかったので Wolfram Alpha を使いました。

solve x = t^a * exp(-b * t) / eta for t

結果です。 $W$ は Lambert W-function あるいは product log function と呼ばれている関数です。

$t = - \frac{α}{β} W (- \frac{β}{α} {(x η)}^{1 / α}), η = E (\frac{α}{β})$

正しい値がでるのか試しました。

import numpy
import matplotlib.pyplot as pyplot
import scipy.special.lambertw as lambertw

def getTime(α, β, x, normalize, k=0):
    return -α * lambertw(-β * (x * normalize)**(1 / α) / α, k) / β

def expPoly(α, β, time):
    return time**α * numpy.exp(-β * time)

def expPolyNormalized(α, β, time):
    normalize = expPoly(α, β, α / β)
    return (
        time**α * numpy.exp(-β * time) / normalize,
        normalize,
    )

samplerate = 48000
duration = 8

time = numpy.linspace(0, duration, duration * samplerate)
alpha = 1
beta = 1

curve, normalize = expPolyNormalized(alpha, beta, time)

xx = numpy.linspace(1, 0, 10)
tt0 = getTime(alpha, beta, xx, normalize, 0)
value_tt0, _ = expPolyNormalized(alpha, beta, tt0)

# k = 0 以外の場合は省略。

pyplot.plot(time, curve)
pyplot.scatter(tt0, value_tt0, color="red", label="k=0")
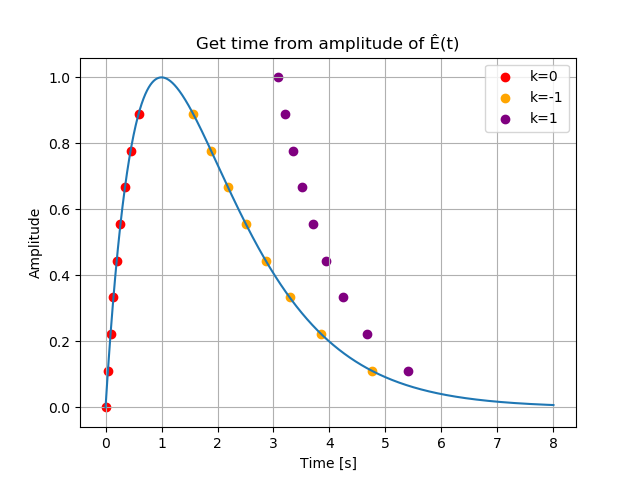
pyplot.show()

結果です。 $k$ は Lambert W-function の引数で、適当な整数です。図を見ると、振幅から時間を求めるときはアタックの区間で $k = 0$ 、ディケイの区間では $k = - 1$ を使えば良さそうです。

Image of determining time t from amplitude of E(t).

$E (t)$ に含まれる $t^{α}$ は浮動小数点数で計算するとそのうち inf になります。そこで $t$ がどこまで進むと $t^{α} \approx + \infty$ となるのかを調べます。

$+ \infty$ になる時点を $t_{\max}$ 、浮動小数点数で表現できる最大値を $F$ とすると、次の式が立ちます。

$t_{\max} = F^{1 / α}$

$α$ が 1 より小さいとき、 $t_{\max}$ は $F$ より大きいので、 $t$ が nan や inf でなければ取り得る全ての値の範囲で計算に問題が無いことが分かります。 $α$ が 1 以上のときの $t_{\max}$ を計算してみます。

import numpy

def printTimeMax(dtype):
    fmax = numpy.finfo(dtype).max
    alpha = numpy.array([2**i for i in range(1, 16)], dtype=dtype)
    timeMax = numpy.power(fmax, dtype(1) / alpha, dtype=dtype)
    print(dtype)
    for a, t in zip(alpha, timeMax):
        print(f"{a:9.1f}, {t}")

printTimeMax(numpy.float32)
printTimeMax(numpy.float64)

整形した出力です。左の列が $α$ 、右の列が $t_{\max}$ です。単精度のときは $α$ が 64.0 のときに 4.0 秒しかレンダリングできないことが分かります。

<class 'numpy.float32'>
      2.0, 1.8446742974197924e+19
      4.0, 4294967296.0
      8.0, 65536.0
     16.0, 256.0
     32.0, 16.0
     64.0, 4.0
    128.0, 2.0
    256.0, 1.4142135381698608
    512.0, 1.1892070770263672
   1024.0, 1.0905077457427979
   2048.0, 1.0442737340927124
   4096.0, 1.0218971967697144
   8192.0, 1.0108892917633057
  16384.0, 1.0054298639297485
  32768.0, 1.002711296081543

<class 'numpy.float64'>
      2.0, 1.3407807929942596e+154
      4.0, 1.157920892373162e+77
      8.0, 3.402823669209385e+38
     16.0, 1.8446744073709552e+19
     32.0, 4294967296.0
     64.0, 65536.0
    128.0, 256.0
    256.0, 16.0
    512.0, 4.0
   1024.0, 2.0
   2048.0, 1.4142135623730951
   4096.0, 1.189207115002721
   8192.0, 1.0905077326652577
  16384.0, 1.0442737824274138
  32768.0, 1.0218971486541166

正規化係数 $E (\frac{α}{β})$ を求めることができる $β$ の範囲です。

$\begin{aligned} t_{\max} & \geq \frac{α}{β} \\ β & \geq \frac{α}{F^{1 / α}} \end{aligned}$

C++ による実装例です。

#include <cmath>
#include <cfloat>

class ExpPolyEnvelope {
public:
  // attack の単位は秒。
  // curve は任意の値。 β に相当。
  // attack と curve が大きいと計算結果が inf になるときがあるので注意。
  void reset(double sampleRate, double attack, double curve)
  {
    alpha = attack * curve;

    auto betaMin = alpha / getTerminationTime();
    if (curve < betaMin) curve = betaMin;

    peak = pow(alpha / curve, alpha) * exp(-alpha);
    gamma = exp(-curve / sampleRate);
    tick = 1.0 / sampleRate;

    time = 0.0;
    value = 1.0;
  }

  bool isReleasing() { return time >= attack; }
  double getTerminationTime() { return pow(DBL_MAX, 1.0 / alpha); }

  double process()
  {
    auto output = pow(time, alpha) * value / peak;
    if (!std::isfinite(output)) return 0.0; // 念のため。
    time += tick;
    value *= gamma;
    return output;
  }

protected:
  double value = 0;
  double peak = 1;
  double gamma = 0;
  double attack = 0;
  double tick = 0;
  double alpha = 0;
  double time = 0;
};

テストコードへのリンクです。

filter_notes/test.cpp at master · ryukau/filter_notes · GitHub

テスト結果です。

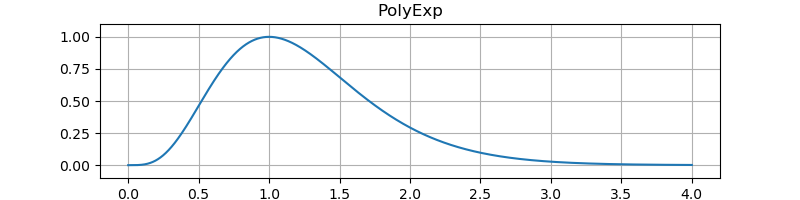
Image of test result of ExpPoly envelope implemented in C++.

ExpPoly エンベロープを GenericDrum の衝突の計算に応用できそうな気がしたので、以下の区間積分が解けるかどうか試しました。

$\begin{matrix} (1) & \int_{τ}^{\infty} t^{α} e^{- β t} d t, τ \geq 0. \end{matrix}$

ここでの応用はエネルギーを時間方向に薄く延ばすことです。つまり、任意の正の実数 $x$ が与えられたときに、式 $1$ と $x$ が等しくなるような $α, β, τ$ の組を知りたいです。

SymPy で積分します。 Maxima の integrate では解けず、 Wolfram Alpha では計算時間切れになりました。

import sympy

t = sympy.Symbol("t", real=True, positive=True)
α = sympy.Symbol("α", real=True, positive=True)
β = sympy.Symbol("β", real=True, positive=True)
τ = sympy.Symbol("τ", real=True, positive=True)

result = sympy.integrate(t**α * sympy.E ** (-β * t), (t, τ, sympy.oo))
print(sympy.latex(result))

出力です。

$τ τ^{α} (\frac{β^{- α - 1} τ^{- α - 1} (α + 1) Γ (- α - 1) γ (α + 1, β τ)}{Γ (- α)} + β^{- α - 1} τ^{- α - 1} Γ (α + 1))$

以下の関数が使われています。

$Γ$ : ガンマ関数。 (Gamma function)
$γ$ : 第 1 種不完全ガンマ関数。 (Lower incomplete gamma function)

整理します。

$\begin{aligned} \int_{τ}^{\infty} t^{α} e^{- β t} d t & = τ^{c} (\frac{s c Γ (- c) γ (c, β τ)}{Γ (- α)} + s Γ (c)), \\ c & = α + 1, \\ s & = β^{- c} τ^{- c} . \end{aligned}$

上の SymPy のコードに以下をつけ足して解こうとしたのですが、 NotImplementedError が出て行き詰りました。

x = sympy.Symbol("x", real=True, positive=True)
sympy.solve(sympy.Eq(result, x), τ)

$E (t)$ は Gamma distribution の PDF の一部と同じ形です。

2024-05-14
- 「区間積分」の節を追加。
- 文章の整理。
2020-03-26
- 既存の用語 exponential polynomial にならって名前を PolyExp から ExpPoly に変更。
- 文章の整理。