何かあれば GitHub のリポジトリに issue を作るか ryukau@gmail.com までお気軽にどうぞ。
Update: 2025-01-07
DR-110のシンバルに似た音を作ります。
次のリンクから完成したコードを読むことができます。
コードを実行するにはPython3と以下のライブラリが必要です。
The Boss DR-110 Dr Rhythm Graphic Information Homepage の Schematics から回路図をダウンロードできます。
richardc64のDR-110のページに回路図の解説があります。
DR-110のシンバルはオシレータから出た信号を High Metal と Low Metal の2つに分けて、それぞれでフィルタとエンベロープをかけてから足し合わせることで合成されます。High Metal と Low Metal という呼び方はrichardc64のDR-110のページにならっています。
今回実装したプログラムの信号の流れです。
4つの矩形波と1つのノイズを足し合わせます。音量の比率は、矩形波がそれぞれ1、ノイズは0.3です。回路図では矩形波の周波数に317、465、820、1150[Hz]が使われています。
そのまま実装すると味気ない音になるので、オシレータの位相を進める時にノイズを加えて周波数を揺らしています。音量の比率も少しだけランダマイズしています。
import numpy as np
import soundfile
import scipy.signal as signal
def normalize(data, peak=1.0):
return peak * data / np.abs(np.max(data))
def pulse(time, frequency):
noise = np.power(10, -(np.random.uniform(0, 5, len(time)) + 5))
return signal.square(2 * np.pi * frequency * (time + noise))
def noise(size):
return np.random.uniform(-1, 1, size)
def randomAmp(low, high):
lowLog = np.log(low)
diffLog = np.log(high) - lowLog
return np.exp(lowLog + diffLog * np.random.random())
def cymbalSource(time, pulseFreq=[317, 465, 820, 1150]):
sig = 0
for freq in pulseFreq:
sig += randomAmp(0.999, 1) * pulse(time, freq)
return sig + noise(len(time)) / 3.3
samplerate = 44100
duration = 2.0
time = np.linspace(0, duration, int(samplerate * duration), endpoint=False)
sig = normalize(cymbalSource(time))
soundfile.write("cymbal_source.wav", sig, samplerate)伝達関数を使ってDR-110の回路図から離散フィルタを設計します。
オシレータセクションで使われているバンドパスフィルタです。BP0とBP1という名前はこの文章で区別するためにつけました。
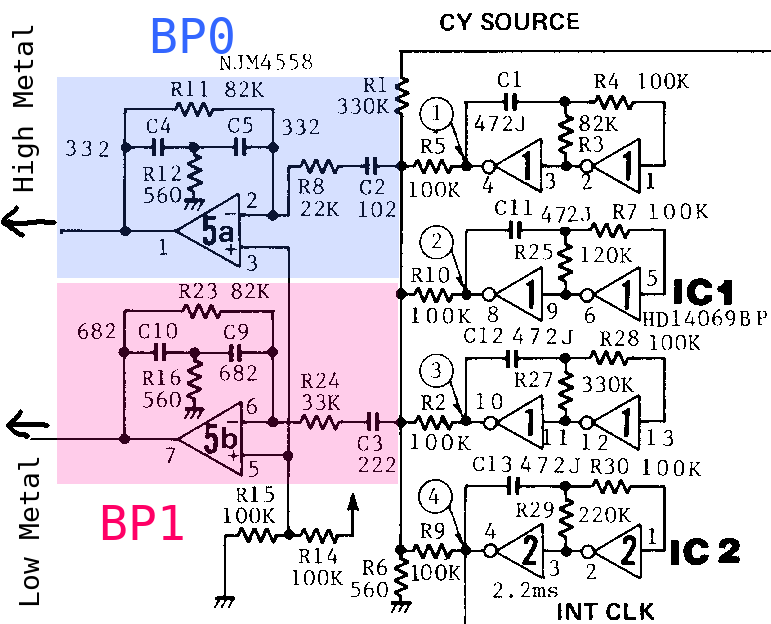
単位の無いキャパシタの値は、上位2桁が有効数字、下位1桁が10の指数で、単位は[pF]です。
バンドパスフィルタの部分だけを抜き出した図です。このフィルタは2つのネットワークが組み合わさっています。
伝達関数 \(H\) です。 \(G\) は抵抗の値で単位は [℧] (mho) あるいは [S] (siemens) 、 \(C\) はキャパシタの値で単位は [F] (ファラド) です。
\[ \begin{aligned} H(s) &= -\frac{y_a(s)}{y_b(s)} \\ y_a(s) &= - \frac{Gs}{s + G / C}\\ y_b(s) &= - k \frac{s^2 + b_0 s + c_0}{s + a_0} \\ a_0 &= \frac{G_2}{C_1 + C_2},\quad b_0 = \frac{G_1 (C_1 + C_2)}{C_1 C_2},\quad c_0 = \frac{G_1 G_2}{C_1 C_2},\quad k = \frac{C_1 C_2}{C_1 + C_2}\\ \end{aligned} \]
伝達関数の式は以下を参考にしました。
Maximaで解きます。 例としてBP0の抵抗とキャパシタの値を使っています。
pico: 10**-12;
G: 1 / 22000;
C: 10 * 10**2 * pico;
G_1: 1 / 82000;
G_2: 1 / 560;
C_1: 33 * 10**2 * pico;
C_2: 33 * 10**2 * pico;
a_0: G_2 / (C_1 + C_2);
b_0: G_1 * (C_1 + C_2) / (C_1 * C_2);
c_0: G_1 * G_2 / (C_1 * C_2);
k: C_1 * C_2 / (C_1 + C_2);
y_a: - G * s / (s + G / C);
y_b: - k * (s**2 + b_0 * s + c_0) / (s + a_0);
rat(- y_a / y_b);出力です。
/* bp0 */
-(94710000000*s^2+25625000000000000*s)/(3437973*s^3+181681500000*s^2+8030000000000000*s+312500000000000000000)
/* bp1 */
-(268345000000*s^2+35234375000000000*s)/(30108309*s^3+522707500000*s^2+15667187500000000*s+195312500000000000000)得られた値を scipy.signal.cont2discrete
に渡すことで離散フィルタを設計できます。下のコードではMaximaで計算した値を
applyContinuousFilter の system
に渡しています。
import numpy
import soundfile
import scipy.signal as signal
def applyContinuousFilter(samplerate, source, system):
num, den, dt = signal.cont2discrete(system, 1.0 / samplerate)
return signal.lfilter(num[0], den, source)
def highMetalFilter(samplerate, source):
return applyContinuousFilter(samplerate, source, (
[9.471e+10, 2.5625e+16, 0],
[3437973.0, 1.816815e+11, 8.03e+15, 3.125e+20],
))
def lowMetalFilter(samplerate, source):
return applyContinuousFilter(samplerate, source, (
[2.68345e+11, 3.5234375e+16, 0],
[30108309.0, 5.227075e+11, 1.56671875e+16, 1.953125e+20],
))
samplerate = 44100
source = numpy.random.uniform(-0.1, 0.1, samplerate * 2)
dest_high_metal = highMetalFilter(samplerate, source)
dest_low_metal = lowMetalFilter(samplerate, source)
soundfile.write("source.wav", source, samplerate)
soundfile.write("dest_high_metal.wav", dest_high_metal, samplerate)
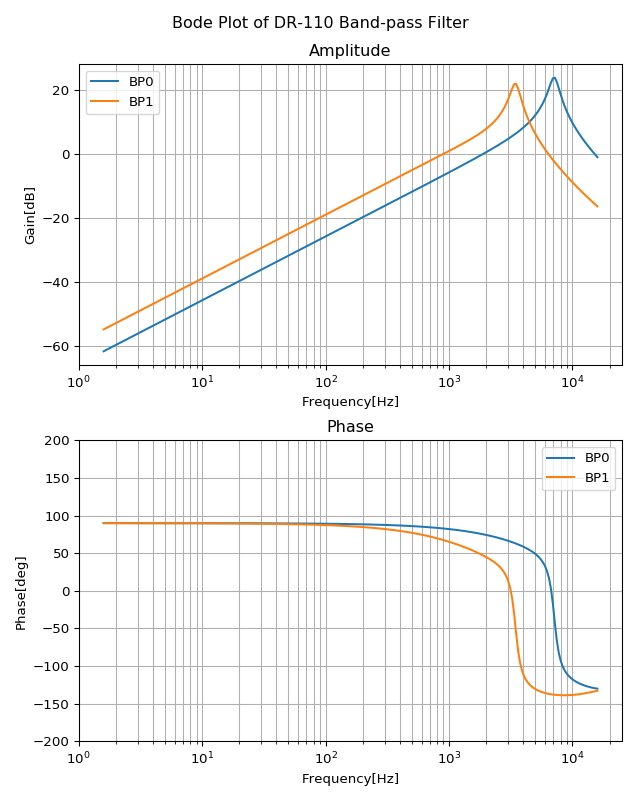
soundfile.write("dest_low_metal.wav", dest_low_metal, samplerate)BP0とBP1のボード線図です。
回路図のいたるところに出てくる1次のハイパスフィルタです。
下図はDR-110のシンバルのエンベロープに関する回路図です。網掛けの色ごとに別のハイパスフィルタを表しています。灰色の矢印は音の信号の流れを表しています。
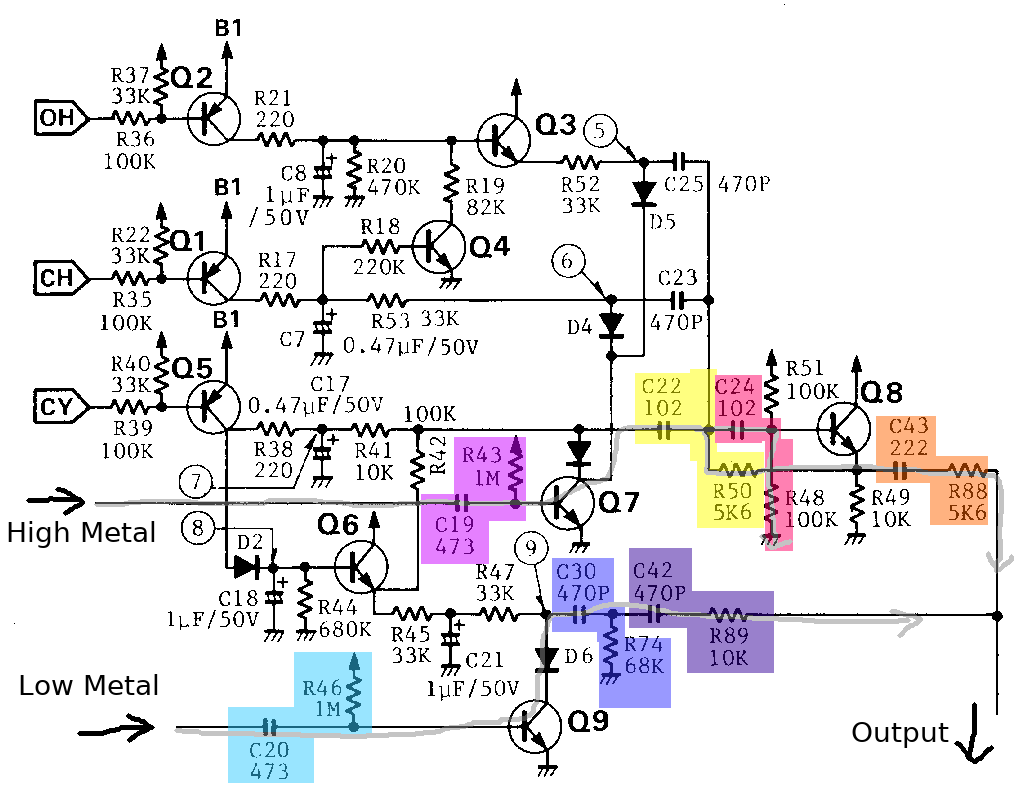
ハイパスフィルタの部分だけを抜き出した図です。
伝達関数 \(H\) です。 \(R\) は抵抗の値で単位は[Ω]、\(C\)はキャパシタの値で単位は[F]です。
\[ H(s) = \frac{RC}{RCs + 1} \]
scipy.signal を使った実装の例です。
import numpy
import soundfile
import scipy.signal as signal
def rcHighpass(samplerate, source, r, c):
rc = r * c
num, den, dt = signal.cont2discrete(([rc, 0], [rc, 1]), 1.0 / samplerate)
return signal.lfilter(num[0], den, source)
samplerate = 44100
resistance = 1e6
capacitance = 47e-9
source = numpy.random.uniform(-0.1, 0.1, samplerate * 2)
dest = rcHighpass(samplerate, source, resistance, capacitance)
soundfile.write("source.wav", source, samplerate)
soundfile.write("dest.wav", dest, samplerate)High Metalはハイハットで使われるフィルタネットワークです。
Low Metalはシンバルの音の低い部分の表現に使われるフィルタネットワークです。
エンベロープの手前での周波数応答です。
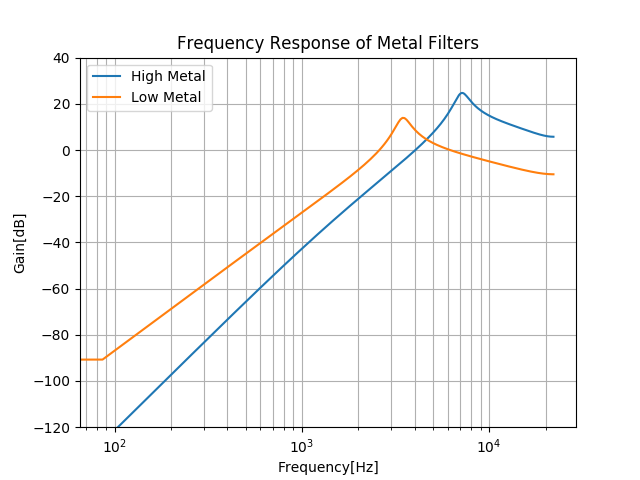
DR-110の回路図から抜き出したシンバルのエンベロープの仕様です。
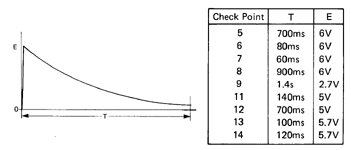
ここではエンベロープに指数的減衰 (Exponential Decay) を使います。
\[ y(t) = x(t)e^{at} \]
\(a < 0\) のときに係数 \(e^{at}\) が指数的減衰を表します。 \(x(t)\) は任意の入力信号です。
\(t = 0\) のときの初期値が \(E\) かつ、 \(t = T\) のとき閾値 \(\epsilon\) になるように \(a\) を決めます。 \(1000\) は \(T\) の単位 [ms] のミリから来ています。
\[ \begin{aligned} \epsilon &= E e^{aT / 1000}\\ \log \left( \frac{\epsilon}{E} \right) &= aT / 1000\\ \frac{1000}{T} \log \left( \frac{\epsilon}{E} \right) &= a \end{aligned} \]
NumPyでの実装は次のようになります。 threshold
の値は適当に決めています。
import numpy
import soundfile
def envelope(time, T, E, threshold=0.4):
a = numpy.log(threshold / E) / T * 1000
return numpy.exp(a * time)
samplerate = 44100
duration = 1
num_sample = int(duration * samplerate)
time = numpy.linspace(0, 1, num_sample)
source = numpy.random.uniform(-0.1, 0.1, num_sample)
dest = source * envelope(time, 700, 6)
soundfile.write("source.wav", source, samplerate)
soundfile.write("dest.wav", dest, samplerate)DR-110ではクローズドハイハット (CH) 、オープンハイハット (OH) 、シンバル (CY) の3つの音が使えます。この3つの音の違いはエンベロープとミックスです。
ハイハットの合成には High Metal からの出力だけを使います。エンベロープの Check Point はクローズドが6、オープンは5です。
シンバルの合成には High Metal と Low Metal の出力を使います。High Metal は Check Point 7, 8 のエンベロープを 10:1 の比率で足し合わせます。 Low metal のエンベロープは Check Point 9です。High MetalとLow Metalは約2:1の比率で足し合わせます。
以下は完成したコードのミックスの部分へのリンクです。
オシレータの音です。
フィルタを通した音です。
ミックスした音です。
オリジナルのDR-110の音です。
作った音はノイズが足りていないように聞こえたので、オシレータのノイズの音量を0.3から6に変えてレンダリングした音です。
アタックが弱いです。エンベロープが単純な指数的減衰ではないのかもしれません。
シンバルのミックスの後に続く回路を無視しています。実機ではBalanceで大きく音が変わります。
トランジスタの回路がよく分からなかったのでハイパスフィルタを適当に試行錯誤して設計しました。
エンベロープを打ち切る電圧がわかっていません。
バンドパスフィルタを伝達関数から離散フィルタにするとき、ソルバが次のようなWarningを出します。
/__somewhere__/scipy/linalg/basic.py:40: RuntimeWarning: scipy.linalg.solve
Ill-conditioned matrix detected. Result is not guaranteed to be accurate.
Reciprocal condition number/precision: 1.5222285969682624e-17 / 1.1102230246251565e-16
RuntimeWarning)