何かあれば GitHub のリポジトリに issue を作るか ryukau@gmail.com までお気軽にどうぞ。
Update: 2025-01-07
今まで適当にやっていたダウンサンプリングについて調べたことをまとめました。
異なる複数のサンプリング周波数の信号を扱うシステムをマルチレートシステム (multirate system) といいます。
ここではサンプリング周波数を下げる処理のことをダウンサンプリング (down-sampling) 、上げる処理のことをアップサンプリング (up-sampling) と呼びます。
ダウンサンプリングを行うためにデシメータ (decimator) とフィルタを組み合わせた部品のことをダウンサンプラ (down-sampler) 、アップサンプリングを行うためにエクスパンダ (expander) とフィルタを組み合わせた部品のことをアップサンプラ (up-sampler) と呼びます。
デシメータは信号を間引いてサンプリング周波数を \(1/M\) 倍に下げる部品、エクスパンダは信号に 0 を付け足してサンプリング周波数を \(L\) 倍に上げる部品のことです。下の図はデシメータとエクスパンダによる時間領域での信号の変換を示した図です。
デシメータとエクスパンダの処理の意味は、変換後の信号の周波数成分の変化を見るとわかりやすいです。デシメータはナイキスト周波数以内の成分の周波数を \(M\) 倍に広げます。このとき周波数成分がナイキスト周波数を超える位置に動くので折り返しが起こります。エクスパンダはナイキスト周波数を超える位置にある鏡像を含む、すべての成分の周波数を \(1/L\) 倍にします。このため元の周波数成分の鏡像がナイキスト周波数以内に入り込んできます。
上の図の赤い実線は正と負のナイキスト周波数以内の成分です。赤い点線はナイキスト周波数を超えた周波数に現れる、元の成分の鏡像を表しています。アップサンプラとダウンサンプラのフィルタは、上の図のナイキスト周波数である \([-1,1]\) の範囲に現れる不要な折り返しや入り込みを消すために必要となります。
アップサンプラは補間器 (interpolator) と呼ばれることがあります。ややこしいのですが、ダウンサンプラのことを指してデシメータと呼ぶこともあるようです。つまり、デシメータは信号を間引くだけの部品を指すこともあれば、間引きとフィルタを組み合わせた部品を指すこともあります。今回参考にした Vaidyanathan による Multirate Digital Filters, Filter Banks, Polyphase Networks, and Applications: A Tutorial では信号を間引くだけの部品のことをデシメータと呼んでダウンサンプラと区別しているので、この文章もそれにならっています。
以下のブロック線図で表される noble identities と呼ばれる恒等式があります。
また、伝達関数 \(H(z)\) が有理関数のとき、以下の式のようにポリフェイズ分解できます。
\[ \begin{aligned} H(z) &= \sum_{\ell=0}^{M-1} z^{-\ell} \left( \sum_{n=-\infty}^{\infty} h(nM + \ell) z^{-nM} \right) \qquad && \text{Type 1 polyphase}\\ H(z) &= \sum_{\ell=L-1}^{0} z^{-\ell} \left( \sum_{n=-\infty}^{\infty} h(nL + \ell) z^{-nL} \right) \qquad && \text{Type 2 polyphase}\\ \end{aligned} \]
FIR の場合、 \(h(n)\) は前から \(n\) 番目のフィルタ係数です。例えば \(H(z) = b_0 + b_1 z^{-1} + b_2 z^{-2} + \dots\) のとき、 \(h(0) = b_0,\;h(1) = b_1,\;h(2) = b_2,\;\dots\) となります。 IIR もポリフェイズ分解できるそうですが設計方法がよくわからなかったのでここでは扱っていません。
Type 1 polyphase の式はダウンサンプリングの計算に使います。例えば \(M=2\) のときはフィルタ係数を以下の 2 組に分解できます。
\[ \begin{aligned} E_0(z) = h(0) + h(2) z^{-1} + h(4) z^{-2} + \dots\\ E_1(z) = h(1) + h(3) z^{-1} + h(5) z^{-2} + \dots\\ \end{aligned} \]
Type 2 polyphase の式はアップサンプリングの計算で使います。 Type 1 polyphase の式では \(\ell\) が \(0, \dots, M-1\) と増えていきますが、 type 2 polyphase の式では \(L-1, \dots, 0\) と減っていきます。つまり分解したフィルタを計算する順番がダウンサンプリングのときとは逆になります。
Noble identities とポリフェイズ分解の式から以下ようにブロック線図を変形できます。
上の図の \(z^{-1}\) が縦に連なっている箇所は、入力 1 サンプルごとに通過させるフィルタ \(E_\ell\) を切り替える処理と考えることができます。つまり \(H(z)\) を長さ \(N\) の FIR フィルタとすると、入力 1 サンプルあたりの計算量を \(N\) から \(N/M\) または \(N/L\) に減らすことができます。
ここでは楽器のシンセサイザの出力のダウンサンプリングが目的なので、ローパスフィルタだけについて見てきます。大まかに以下の 4 種類のローパスフィルタがダウンサンプリングに使えそうです。
| 種類 | 特長 |
|---|---|
| FIR Polyphase | 線形位相。群遅延大。 |
| IIR Direct | 群遅延小。 |
| IIR Polyphase (Approximately Linear-Phase) | ほぼ線形位相。群遅延大。要補正フィルタ。 |
| IIR Polyphase (Nonlinear-Phase) | 群遅延小。要補正フィルタ。 |
FIR ポリフェイズは設計も実装も簡単ですが、ダウンサンプリングの倍率が大きくなるとフィルタを長くする必要が出てくるので遅くなります。設計には急峻なロールオフを達成しやすい Remez アルゴリズムが適しています。窓関数法や最小二乗法は Remez に比べるとロールオフが緩やかになる傾向があります。 FIR の欠点は群遅延の大きさです。群遅延の大きさは、そのままレイテンシの大きさになります。
IIR を直接計算する方法の利点は群遅延が小さいことです。またダウンサンプリングの倍率が高いときは FIR よりも計算が速くなる傾向があります。 IIR は線形位相でないという欠点がありますが、人間の耳は位相に対する感度がよくないと言われているので、音に使うなら問題になりにくいと考えられます。設計にはロールオフが急峻な楕円フィルタが適しています。以下の表に古典的な IIR フィルタの特徴についてまとめています。
| IIR の種類 | 特徴 |
|---|---|
| Butterworth | リップル無し。緩やかなロールオフ。ストップバンドは単調に減衰。 |
| Chebyshev Type 1 | パスバンドにリップル。ストップバンドは単調に減衰。 |
| Chebyshev Type 2 | パスバンドは平坦。ストップバンドにリップル。 |
| Elliptic (楕円) | パスバンドとストップバンドにリップル。急峻なロールオフ。位相特性が悪い。 |
IIR
ポリフェイズは設計方法がよくわからなかったので、ここでは実装していません。ほぼ線形位相
(approximately linear-phase) と非線形位相 (nonlinear-phase) の 2
種類があるようです。詳細は以下のリンクを参照してください。 2
倍のダウンサンプリングであれば MATLAB に dsp.IIRHalfbandDecimator
という関数があります。
サンプリング周波数を \(f_s\) 、ダウンサンプリングの倍率を \(M\) とすると、ローパスフィルタのストップバンド周波数 \(f_\sigma\) を \(\dfrac{f_s}{2M}\) より小さくしてオーバーラップを無くすかどうかの選択肢が出てきます。多少はエイリアシングがあってもいいなら \(f_\sigma \geq \dfrac{f_s}{2M}\) とすることで、フィルタのロールオフに余裕を持たせることができます。エイリアシングを完全に止めるなら \(f_\sigma < \dfrac{f_s}{2M}\) として帯域がオーバーラップしないようにします。
人間の可聴域の上限は 20000 Hz と言われています。なので、例えばサンプリング周波数が 48000 Hz なら可聴域の上限 20000 Hz からナイキスト周波数 24000 Hz まで 4000 Hz の区間はエイリアシングが出ていても普通の人には聞こえません。個人差がありますが 16000 Hz より高い音は聞こえにくくなる傾向があるので、パスバンド周波数を 20000 Hz より低く下げることも考えられます。以下のリンクの table 1 を参照してみてください。
計算量を節約するときは Butterworth フィルタのように振幅特性が単調に減衰するフィルタを使うことで低域に折り返しが入り込むことだけは防ぐという設計も考えられます。
まず以下の仕様を決めます。
ここでは出力信号のサンプリング周波数を 48000 Hz で統一しています。
以下のコードで scipy.signal.remez
を使って設計します。
import scipy.signal as signal
import numpy as np
def decimationFir(length, oversample, cutoff, nyquist=0.5):
"""オーバーラップありのときは nyquist を 0.6 などに設定する。"""
bands = np.hstack((
[0, cutoff],
[nyquist, oversample / 2],
))
desired = (1, 0)
return signal.remez(length, bands, desired, fs=oversample)length はフィルタの長さ (タップ数) です。
oversample はオーバーサンプリングの倍率です。例えば
oversample = 2 のときは 1/2
倍のダウンサンプリングに使うフィルタを設計します。
cutoff はナイキスト周波数が 0.5
に正規化されているときのカットオフ周波数です。例えばサンプリング周波数
48000 Hz 、カットオフ周波数 20000 Hz のときは cutoff
の値を 20000 / 48000 = 0.4 と設定できます。
オーバーラップありのときは nyquist を 0.5
以上の値にします。以下のコードでオーバーラップあり、ストップバンドの低減が
-60 dB
のフィルタが設計できます。フィルタの長さが短くできるのがオーバーラップありの利点です。
fir = decimationFir(68, 4, 0.4, 0.6)oversample = 2, cutoff = 0.375
のときに、ストップバンドの低減が大まかに -60, -80, -100, -120 dB
となる値を下の表にまとめました。 oversample = 4
のときは下の表のフィルタの長さを 2
倍にすると同じ特性が得られます。同様に oversample = 8
のときは 4 倍、 oversample = 16 のときは 8
倍にすると同じ特性が得られます。
| 低減 [dB] | フィルタの長さ |
|---|---|
| -60 | 54 |
| -80 | 76 |
| -100 | 98 |
| -120 | 120 |
例えば oversample = 4 でストップバンドの低減が -60 dB
のときは、フィルタの長さを 54 * 2 = 108
にすれば所望の特性が得られます。
fir = decimationFir(108, 4, 0.375)以下は上のコードで設計した FIR フィルタの振幅特性です。
ポリフェイズ分解した FIR フィルタを用いた 1/2 倍のダウンサンプリングの実装例です。
#include <array>
#include <iostream>
#include <numeric>
#include <vector>
/*
2 倍のオーバーサンプリングに特化した FIR フィルタ係数。
パスバンドに ±0.003 dB のリップル。
ストップバンドで -69 dB 低減。
オーバーラップ無し。
---python
import scipy.signal as signal
oversample = 2
signal.remez(64, [0, 0.375, 0.5, oversample], [1, 0], fs=oversample)
---
*/
template<typename Sample> struct FirRemez64Decimation2 {
constexpr static size_t bufferSize = 32;
constexpr static size_t nPhase = 2;
constexpr static std::array<std::array<Sample, bufferSize>, nPhase> coefficient{{
{Sample(-0.00012586358900962356), Sample(0.0001828145651312807),
Sample(8.205416319885108e-05), Sample(-0.0007239553549487794),
Sample(0.0018923639640423555), Sample(-0.00353192867622875),
Sample(0.005331459582347676), Sample(-0.006667992332855854),
Sample(0.006636334343333397), Sample(-0.004162169091786725),
Sample(-0.0018313041529962014), Sample(0.012291623826628002),
Sample(-0.02812500771752753), Sample(0.05102267479538475),
Sample(-0.08758235952225661), Sample(0.18605559261058696),
Sample(0.4035431721330982), Sample(-0.03627960335535102),
Sample(-0.006631516329342658), Sample(0.02064755543805059),
Sample(-0.023817278019366648), Sample(0.021451149873294335),
Sample(-0.0164261830615856), Sample(0.010706859341764241),
Sample(-0.005602179907252967), Sample(0.001817817136086864),
Sample(0.00046580645271121403), Sample(-0.0014510531292568874),
Sample(0.0015411334474003102), Sample(-0.0011736418939169283),
Sample(0.0006849141024872853), Sample(-0.00039292037784520776)},
{Sample(-0.00039292037784520776), Sample(0.0006849141024872853),
Sample(-0.0011736418939169283), Sample(0.0015411334474003102),
Sample(-0.0014510531292568874), Sample(0.00046580645271121403),
Sample(0.001817817136086864), Sample(-0.005602179907252967),
Sample(0.010706859341764241), Sample(-0.0164261830615856),
Sample(0.021451149873294335), Sample(-0.023817278019366648),
Sample(0.02064755543805059), Sample(-0.006631516329342658),
Sample(-0.03627960335535102), Sample(0.4035431721330982),
Sample(0.18605559261058696), Sample(-0.08758235952225661),
Sample(0.05102267479538475), Sample(-0.02812500771752753),
Sample(0.012291623826628002), Sample(-0.0018313041529962014),
Sample(-0.004162169091786725), Sample(0.006636334343333397),
Sample(-0.006667992332855854), Sample(0.005331459582347676),
Sample(-0.00353192867622875), Sample(0.0018923639640423555),
Sample(-0.0007239553549487794), Sample(8.205416319885108e-05),
Sample(0.0001828145651312807), Sample(-0.00012586358900962356)},
}};
};
template<typename Sample, typename FIR> class FirFilter {
std::array<std::array<Sample, FIR::bufferSize>, FIR::nPhase> buf;
public:
FirFilter() { reset(); }
void reset()
{
for (auto &bf : buf) bf.fill(Sample(0));
}
Sample process(std::array<Sample, FIR::nPhase> &input)
{
Sample sum = 0;
for (size_t ph = 0; ph < FIR::nPhase; ++ph) {
auto &bf = buf[ph];
for (size_t i = 0; i < bf.size() - 1; ++i) bf[i] = bf[i + 1];
bf.back() = input[ph];
const auto &fir = FIR::coefficient[ph];
for (size_t i = 0; i < fir.size(); ++i) sum += bf[i] * fir[i];
}
return sum;
}
};
int main()
{
FirFilter<float, FirRemez64Decimation2<float>> filter;
std::vector<float> data(64);
std::iota(data.begin(), data.end(), 0.0f);
std::array<float, 2> input;
for (size_t i = 0; i < data.size(); i += 2) {
input[0] = data[i];
input[1] = data[i + 1];
std::cout << filter.process(input) << "\n";
}
return 0;
}上の実装では FirFilter にリングバッファ
buf を持たせて、入力サンプルごとに回しています。
auto &bf = buf[ph];
for (size_t i = 0; i < bf.size() - 1; ++i) bf[i] = bf[i + 1];
bf.back() = input[ph];この回転は std::rotate に置き換えられます。
auto &bf = buf[ph];
std::rotate(buf.begin(), buf.begin() + 1, buf.end());
bf.back() = input[ph];簡単なベンチマークを取ったところ、バッファの長さが 16 のときは
for で回す実装が速いですが、バッファの長さが 32
を超えると std::rotate
のほうが速かったです。この結果は環境によって変わると思われるので参考程度に留めておいてください。
またリングバッファを回さず、事前に回しておいたフィルタ係数を畳み込む実装も考えられます。例えば
[0, 1, 2, 3]
というフィルタ係数が与えられたとき、以下のような配列を作ります。
[
[0, 1, 2, 3],
[1, 2, 3, 0],
[2, 3, 0, 1],
[3, 0, 1, 2],
]畳み込む方向によっては内側の配列の前後が
[3, 2, 1, 0], [0, 3, 2, 1], ... のように反転します。
私の環境では事前に回しておく実装のほうが速かったです。以下のリンクから実装が読めます。
まず以下の仕様を決めます。
ここでは出力信号のサンプリング周波数を 48000 Hz で統一しています。
オーバーラップ無しのときは楕円フィルタが適しています。以下のコードで楕円ローパスフィルタを設計できます。
import scipy.signal as signal
import numpy as np
order = 12 # フィルタの次数。
ripple = 0.01 # パスバンドのリップルの大きさ。単位は dB 。
attenuation = 100 # ストップバンドでの低減。単位は dB 。
cutoff = 0.4 # カットオフ周波数。 fs = 1 に正規化された周波数。
oversample = 2 # オーバーサンプリングの倍率。
sos = signal.ellip(
order, ripple, attenuation, cutoff, "low", output="sos", fs=oversample)下の表に ripple = 0.01 、 cutoff = 0.4
でオーバーサンプリングの倍率とストップバンドでの低減を変えたときにオーバーラップしない最小の次数をまとめています。
| 倍率 | 低減 [dB] | 次数 |
|---|---|---|
| 2 | -60 | 8 |
| 2 | -80 | 9 |
| 2 | -100 | 12 |
| 2 | -120 | 12 |
| 4 | -60 | 8 |
| 4 | -80 | 10 |
| 4 | -100 | 12 |
| 4 | -120 | 13 |
| 8 | -60 | 9 |
| 8 | -80 | 10 |
| 8 | -100 | 12 |
| 8 | -120 | 13 |
| 16 | -60 | 9 |
| 16 | -80 | 10 |
| 16 | -100 | 12 |
| 16 | -120 | 14 |
ripple = 0.01 、 cutoff = 0.4
のとき、次数 12
の楕円フィルタはいろいろなオーバーサンプリングの倍率に対応できて便利そうです。
オーバーラップありのときは Butterworth フィルタも使えます。以下のコードで Butterworth ローパスフィルタを設計できます。
import scipy.signal as signal
import numpy as np
order = 8 # フィルタの次数。
cutoff = 0.4 # カットオフ周波数。 fs = 1 に正規化された周波数。
oversample = 2 # オーバーサンプリングの倍率。
sos = signal.butter(order, cutoff, "low", output="sos", fs=oversample)以下は cutoff = 0.4 の Butterworth
フィルタを使ったときの一回目の折り返しの低減量のプロットです。 4
倍以上のオーバーサンプリングでは、次数が 1 増えるごとに折り返しが -6
dB 低減されます。 2
倍のときはバイリニア変換による周波数の歪みが大きいので、低減量の傾きが急になっています。サンプリング周波数
\(f_s\) が 48000 Hz のとき \(f_s/4\) は 12000 Hz 、 \(f_s/8\) は 6000 Hz です。
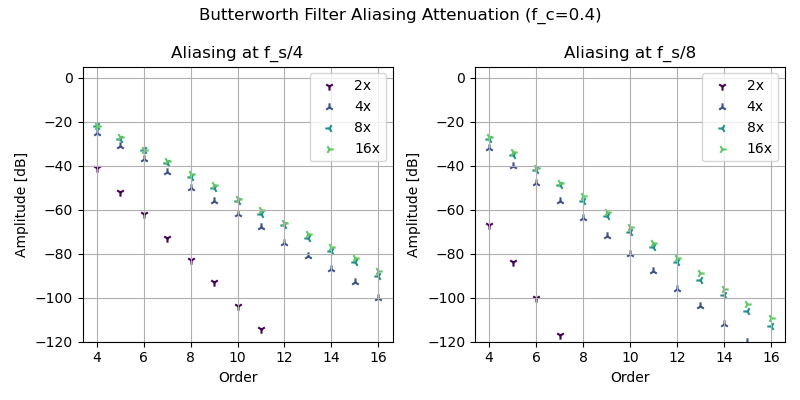
\(f_s/8\) で -60 dB の低減が欲しいときは 8 次の Butterworth フィルタで十分そうです。
IIR フィルタを用いた 1/8 倍のダウンサンプリングの実装例です。
#include <array>
#include <iostream>
#include <numeric>
#include <vector>
/*
---python
import numpy
from scipy import signal
sos = signal.ellip(12, 0.01, 100, 0.4, "low", output="sos", fs=8)
---
*/
template<typename Sample> struct SosEllipticDecimation8 {
constexpr static size_t nSection = 6;
constexpr static std::array<std::array<Sample, 5>, nSection> co{{
{Sample(2.0478175697515062e-05), Sample(5.313899743869536e-06),
Sample(2.047817569751506e-05), Sample(-1.7517115385026274),
Sample(0.7700392502488301)},
{Sample(1.0), Sample(-1.438980096034124), Sample(1.0), Sample(-1.774966834164871),
Sample(0.8105614413580351)},
{Sample(1.0), Sample(-1.7274028784750513), Sample(1.0), Sample(-1.808053369266683),
Sample(0.867640704095363)},
{Sample(1.0), Sample(-1.8120823742998813), Sample(1.0000000000000004),
Sample(-1.8388054096377313), Sample(0.9192163691033324)},
{Sample(1.0), Sample(-1.8441397779182482), Sample(1.0000000000000002),
Sample(-1.8637392843186766), Sample(0.9580528037069385)},
{Sample(1.0), Sample(-1.855844538281174), Sample(1.0), Sample(-1.8856454058448944),
Sample(0.9871065355804314)},
}};
};
// SOS: Second order sections.
template<typename Sample, typename IIR, size_t oversample = 8> class SosFilter {
public:
void reset()
{
x1.fill(0);
x2.fill(0);
y1.fill(0);
y2.fill(0);
}
void push(Sample input)
{
for (size_t i = 0; i < IIR::nSection; ++i) {
// clang-format off
auto y0 =
+ IIR::co[i][0] * input
+ IIR::co[i][1] * x1[i]
+ IIR::co[i][2] * x2[i]
- IIR::co[i][3] * y1[i]
- IIR::co[i][4] * y2[i];
// clang-format on
x2[i] = x1[i];
x1[i] = input;
y2[i] = y1[i];
y1[i] = y0;
input = y0;
}
}
inline Sample output() { return y1[IIR::nSection - 1]; }
Sample process(const std::array<Sample, oversample> &input)
{
for (const auto &value : input) push(value);
return output();
}
std::array<Sample, IIR::nSection> x1{};
std::array<Sample, IIR::nSection> x2{};
std::array<Sample, IIR::nSection> y1{};
std::array<Sample, IIR::nSection> y2{};
};
int main()
{
SosFilter<float, SosEllipticDecimation8<float>> filter;
std::vector<float> data(64);
std::iota(data.begin(), data.end(), 0.0f);
std::cout << "\n--- Use `process` to process each n samples at once.\n";
std::array<float, 8> input;
for (size_t i = 0; i < data.size(); i += 8) {
for (size_t j = 0; j < input.size(); ++j) input[j] = data[i + j];
std::cout << filter.process(input) << "\n";
}
std::cout << "\n--- Use `push` and `output` to get output for each sample.\n";
filter.reset();
for (size_t i = 0; i < data.size(); ++i) {
filter.push(data[i]);
if (i % 8 == 7) std::cout << filter.output() << "\n";
}
return 0;
}SosEllipticDecimation8::co
がフィルタ係数です。フィルタ係数は 2 次セクション (second order
sections, sos) 形式で、以下のように並んでいます。
{{
{b0, b1, b2, a1, a2}, // Section 0
{/* ... */}, // Section 1
{/* ... */}, // Section 2
// ...
}}b0 、 b1 、 b2
は伝達関数の分母の係数、 a1 、 a2
は伝達関数の分子の係数です。 a0 はすべて 1
に正規化されているので計算を省いています。
\[ H(z) = \frac{b_0 + b_1 z^{-1} + b_2 z^{-2}}{1 + a_1 z^{-1} + a_2 z^{-2}} \]
SOSFilter は direct
form I の実装です。 Direct form II
も試したのですが、今回の実装では direct form I
よりも少し遅かったです。
サンプリング周波数の変換をマルチステージにするという手法があります。例えば 1/8 倍のダウンサンプリングであれば、1/2 倍と 1/4 倍の 2 ステージ、あるいは 1/2 倍を 3 回繰り返す 3 ステージ、などに分割することができます。
IIR フィルタを用いた音のダウンサンプリングではマルチステージにすることでノイズを減らせます。試行錯誤の結果、 1 ステージ目に Butterworth のような単調減衰フィルタ、 2 ステージ目にハーフバンド楕円フィルタを使うといいことがわかりました。
以下はマルチステージ構成のブロック線図です。 \(M\) はダウンサンプリングの倍率です。
以下はローパスフィルタの仕様です。
\(f_s\) を入力信号のサンプリング周波数、 \(f_1\) を 1 ステージ目のデシメーション後のナイキスト周波数、 \(f_2\) を 2 ステージ目のデシメーション後のナイキスト周波数とします。ハーフバンド楕円フィルタは 1/2 倍のダウンサンプリングにしか使えないので \(f_1 = 2 f_2\) です。
1 ステージ目の Butterworth は、周波数 \(3 f_2\) で -140 dB 低減するように設計します。また 2 ステージ目のハーフバンド楕円フィルタもストップバンドで -140 dB 低減するように設計します。
-140 dB というのは、およそ 24 bit の S/N 比です。より正確な値は \(20 \log_{10} 2^{-24} \approx -144.5 \mathrm{[dB]}\) です。 24 bit という数字は IEEE 754 の単精度浮動小数点数の仮数部のビット数から来ています。意外だったのですが、浮動小数点数の値が仮数部のビット数を下回るとノイズが乗ります。原因としてはフィルタの計算での丸め誤差などが考えられます。
以下のリンク先に 1 ステージ目の Butterworth のフィルタ係数と、設計に使った Python 3 のコードがあります。
ハーフバンド楕円の設計と実装については以下の記事を参照してください。
適切なマルチステージの分割を求める手法として Ahmed Shahein さんによる記事の参考文献に挙げられていた以下の論文があるようです。
SosFilter に遅延が追加されていた間違いを修正。