何かあれば GitHub のリポジトリに issue を作るか ryukau@gmail.com までお気軽にどうぞ。
Update: 2025-01-07
Landajuela さんの BURGERS EUQATION で紹介されていた Godunov’s method で変形した Burgers 方程式を実装して音を入力します。
次のリンクからコードをまとめて読むことができます。
リンク先の propagation.py は SoX を使っています。
今回使った Python3 のライブラリです。
ここでシミュレーションするのは inviscid な Burgers 方程式です。
\[ u_t + u u_x = 0 \]
\(u_t, u_x\) は偏微分の表記です。
Landajuela さんの BURGERS EUQATION で紹介されていた Godunov’s method で変形した Burgers 方程式です。
\[ U_j^{n+1} = U_j^n - \frac{k}{h} \left( F(U_j^n, U_{j+1}^n) - F(U_{j-1}^n, U_j^n) \right) \]
\(F(U, V)\) は次のように定義されています。
\[ \begin{aligned} F(U, V) &= \frac{(u^*)^2}{2}\\ \text{If}\;U \geq V\;\text{then}\qquad u^* &= \begin{cases} U, &\text{if}\;\frac{U+V}{2} > 0,\\ V, &\text{in other case.} \end{cases}\\ \text{If}\;U < V\;\text{then}\qquad u^* &= \begin{cases} U, &\text{if}\;U > 0,\\ V, &\text{if}\;V > 0,\\ 0, &\text{if}\;U \leq 0 \leq V. \end{cases} \end{aligned} \]
実装します。
import matplotlib.pyplot as pyplot
import numpy
class Burgers1D:
"""
dx = 1, dt = 1 で固定した inviscid Burgers' equation 。
"""
def __init__(self, length):
"""length はシミュレーションする波の配列の長さ。"""
self.wave = numpy.zeros((2, length))
self.reset()
def u_star(self, u, v):
return numpy.where(
u >= v,
numpy.where((u + v) / 2 > 0, u, v),
numpy.where(u > 0, u, numpy.where(v < 0, v, 0)),
)
def step(self):
self.wave = numpy.roll(self.wave, 1, axis=0)
last = self.wave.shape[1] - 1
wave_l = numpy.roll(self.wave[1], 1)
wave_r = numpy.roll(self.wave[1], -1)
u_star_l = self.u_star(self.wave[1], wave_r)
u_star_r = self.u_star(wave_l, self.wave[1])
self.wave[0] = self.wave[1] - (u_star_l * u_star_l - u_star_r * u_star_r) / 2
self.wave[0][0] = 0
self.wave[0][last] = 0
if self.pick_y != 0:
self.wave[0][self.pick_x] = self.pick_y
def reset(self):
self.wave.fill(0)
def pick(self, x, y):
"""
x の範囲は [0, 1] 。
y の範囲は [-1, 1] 。 |y| > 1 で発散する。
"""
x = max(0, min(x, 1))
self.pick_x = numpy.int32(x * self.wave.shape[1])
self.pick_y = y
def state(self):
return self.wave[0]
length = 512
burgers = Burgers1D(length)
signal = numpy.sin(numpy.linspace(0, 8 * numpy.pi, length))
for i, pick_y in enumerate(signal):
burgers.pick(0, pick_y)
burgers.step()
pyplot.grid()
pyplot.plot(burgers.state())
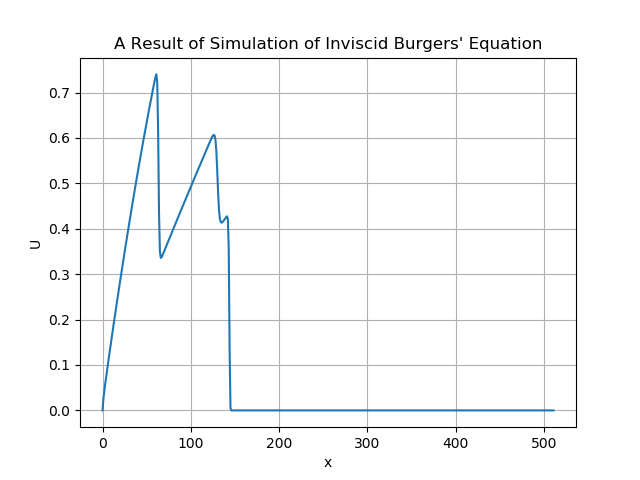
pyplot.show()コードを実行すると次のようなプロットが出力されます。

キャンバスをクリックすると波が起こります。
中央の黒い線は \(U = 0\) を表しています。上半分は \(U > 0\) 、下半分は \(U < 0\) となります。
今回のシミュレーションでは入力の符号によって波が進む方向が決まるようです。
波の進む方向が一方向に固定されるので、入力信号がすべて正の値になるように整形します。またシミュレーションが発散しないように入力信号の最大値が 1 以下となるようにします。
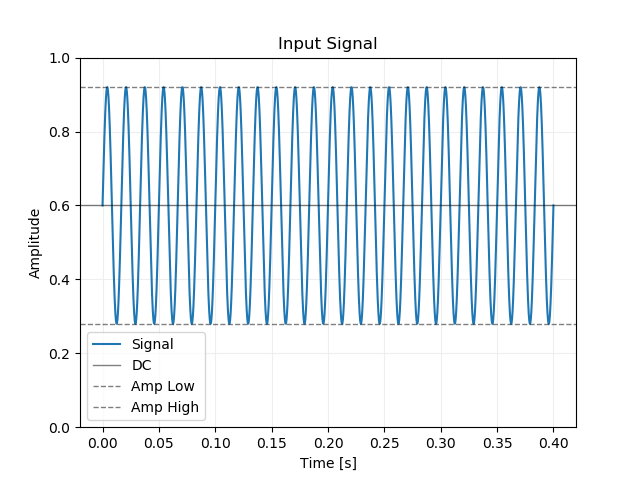
次の図は dc = 0.6 、 amp = 0.8
として整形した入力信号の例です。
上の図の入力信号から得られた inviscid な Burgers 方程式のシミュレーション結果です。
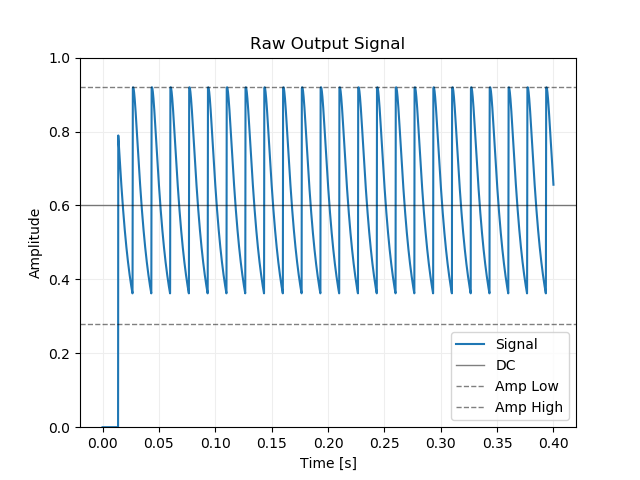
シミュレーションから得られた信号を wav
ファイルとして保存するときに直流を切りたいのですが、このままハイパスフィルタをかけると音の始まりに大きなポップノイズが乗ってしまいます。今回は信号の
numpy.median
の値をしきい値として、信号の開始からしきい値を超えるまでの区間を
numpy.median
の値に置き換えることでポップノイズを抑えました。
実装は次のようになります。
import numpy
import scipy.signal
import soundfile
from burgers import Burgers1D
samplerate = 44100
duration = 0.4
frequency = 60
amp = 0.8
dc = 0.6
phase = numpy.linspace(
0,
2 * numpy.pi * frequency * duration,
int(samplerate * duration),
)
input_signal = numpy.sin(phase)
# 入力信号を整形。
amp = dc * amp if dc < 0.5 else (1 - dc) * amp
signal = (dc - amp) + amp * (input_signal + 1)
input_signal = numpy.copy(signal)
# シミュレーション。
burgers = Burgers1D(257)
read_index = burgers.wave.shape[1] - 2
for i, y in enumerate(signal):
burgers.pick(0, y)
burgers.step()
signal[i] = burgers.state()[read_index]
raw_signal = numpy.copy(signal)
# ポップノイズを防ぐために信号の開始からしきい値を超えるまでの値を置き換え。
threshold = numpy.median(signal)
i = 0
while signal[i] < threshold:
i += 1
signal[:i] = threshold
signal -= threshold
# 直流の除去。
hp_sos = scipy.signal.butter(4, 2 * 20 / samplerate, btype="highpass", output="sos")
signal = scipy.signal.sosfilt(hp_sos, signal)
soundfile.write("output.wav", signal, samplerate)直流を除去した出力信号です。
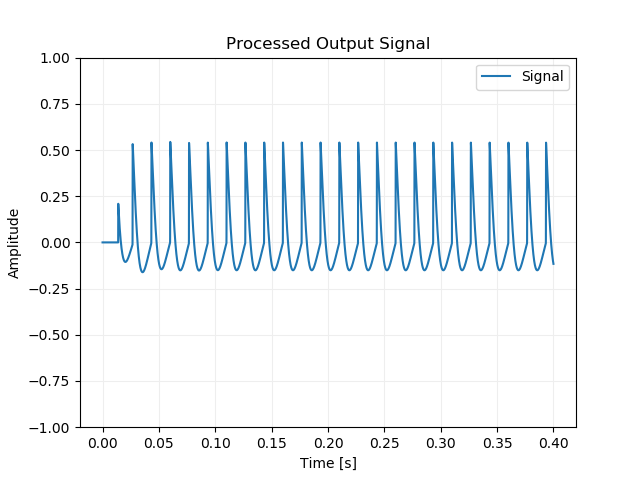
ここまでのコードを propagation.py
にまとめてコマンドラインから使えるようにしました。声のサンプルのラベルに書いている
-d や -l は propagation.py
のオプションです。 -d は DC オフセット、 -l
は Burgers1D のインスタンスを生成するときに渡す
length です。
1000Hz のサイン波の入力信号と Burgers1D
に通した結果です。
ブラウンノイズの入力信号と Burgers1D
に通した結果です。
サイン波とブラウンノイズは SoX で生成しました。
sox -n sin.wav synth 1.0 sine 1000.0
sox -n noise.wav synth 0.5 brownnoiseFreesound で見つけた AlienAudio
さんによる人の声のサンプルを Burgers1D
に通しました。