何かあれば GitHub のリポジトリに issue を作るか ryukau@gmail.com までお気軽にどうぞ。
Update: 2025-01-07
衝撃波が起きるとN波と呼ばれる波形が現れます。N波はBurgers方程式を解くことで近似できます。
Burgers方程式です。TOURNATのIntroductory Lecture on Nonlinear Acousticsで紹介されていた形を使っています。
\[ \frac{\partial p_a}{\partial z} + \frac{1}{c} \frac{\partial p_a}{\partial t} - \frac{b}{2 c_0} \frac{\partial^2 p_a}{\partial t^2} = 0 \]
Burgers方程式の厳密解です。Introductory Lecture on Nonlinear AcousticsのPage 42の参考文献にあるJ.D. Cole, 1951の式(52)から持ってきたようです。
\[ p_a(\xi, \theta) = p_0 \frac{ 4 \Gamma^{-1} \sum_{n=1}^{+\infty} (-1)^{n+1} n I_n(\Gamma / 2) e^{-n^2 \xi / \Gamma} \sin(n \theta) }{ I_0(\Gamma / 2) + 2 \sum_{n=1}^{+\infty} (-1)^{n} I_n(\Gamma / 2) e^{-n^2 \xi / \Gamma} \cos(n \theta) } \]
実装します。
import numpy
import matplotlib.pyplot as pyplot
from scipy.special import iv
def burgers_hopf_cole(xi, theta, gamma, loop=128):
"""
p_a / p_0 を返す。
"""
gamma_div_2 = gamma / 2
xi_div_gamma = xi / gamma
numer = 0
denom = 0
sign = 1
for n in range(1, loop + 1):
iv_exp = iv(n, gamma_div_2) * numpy.exp(-n * n * xi_div_gamma)
n_theta = n * theta
numer += sign * n * iv_exp * numpy.sin(n_theta)
sign = -sign
denom += sign * iv_exp * numpy.cos(n_theta)
return (4 / gamma * numer) / (iv(0, gamma_div_2) + 2 * denom)
theta = numpy.linspace(0, 2 * numpy.pi, 512)
data = burgers_hopf_cole(2, theta, 10)
pyplot.plot(theta, data)
pyplot.grid()
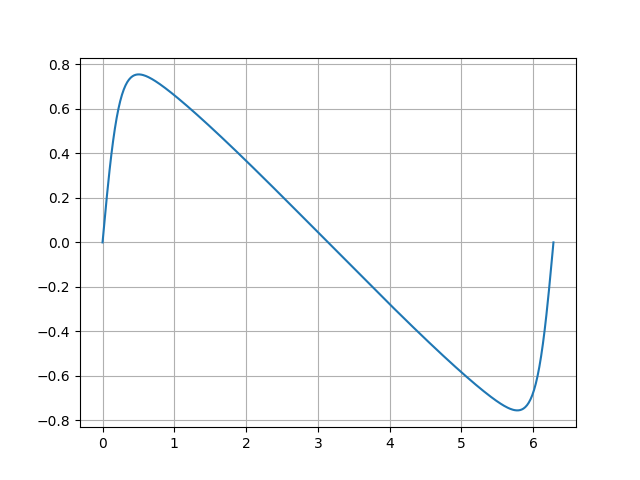
pyplot.show()コードをコピペしてPython3のインタプリタに貼り付ければ次のプロットが出力されます。

Burgers方程式の厳密解の振る舞いを見るために \(\xi = [0, 10]\) 、 \(\Gamma = [1, 30]\) の区間をプロットして動画にしました。動画についている音はプロットした波形をつなぎ合わせたものです。動画のフレームレートにあわせて音の周波数は60Hzにしています。
Burgers方程式の厳密解の波形を見たところmdaDX10というVSTプラグインの波形を思い出したので調べました。
src/mdaDX10.cpp
にあった波形生成の式です。
o += V->cenv * (m * V->mod1 + (x + x * x * x * (w * x * x - 1.0f - w)));エンベロープとFMの計算を取り除いて整理します。
out = x + x * x * x * (w * x * x - 1.0 - w)コメントに “5th-order sine approximation” とあるので \(\sin\) のテイラー展開を使っているように思います。
\[ \sin(x) = x - \frac{x^3}{3!} + \frac{x^5}{5!} + \dots \]
mdaDX10のオシレータの式です。
\[ \mathtt{out}(x, w) = x - (1 + w) x^3 + w x^5 \]
\(x\) はオシレータの位相 [rad/π] で範囲は \([-1, 1]\) 、 \(w\) は波形を変えるパラメータで範囲は \([-2.5, 0.5]\) です。
\(w\) の区間の端で式がどう変わるかを確認します。
\[ \begin{aligned} \mathtt{out}(x, -2.5) &= x + 1.5 x^3 - 2.5 x^5\\ \mathtt{out}(x, 0.5) &= x - 1.5 x^3 + 0.5 x^5 \end{aligned} \]
プロットします。出力波形の絶対値の最大値が1.0になるように正規化しています。
それなりにBurgers方程式の厳密解と似た音が出ています。
動画を書き出したソースコードへのリンクです。