AM による周波数シフト

この文章では虚数を \(j\) で表します。

Scott Wardle さんによる A Hilbert-Transformer Frequency Shifter for Audio で紹介されていた AM による周波数シフトで遊びます。

紹介されていた手法では analytic signal \(s(t)\) に \(e^{j \omega_c t}\) を掛け合わせてから実部を取り出すことで \(\omega_c\) だけ周波数シフトできます。Analytic signal は負の周波数成分が全て0になる信号で、複素数です。

\[ \begin{aligned} y_{\mathtt{shift}} (t) &= \mathrm{Re}(s(t) e^{\pm j \omega_c t})\\ &= \mathrm{Re}(|s(t)| e^{j(\angle s(t) \pm \omega_c t)})\\ &= |s(t)| \cos(\angle s(t) \pm \omega_c t)\\ |s(t)| &= \sqrt{\mathrm{Re}^2(s(t)) + \mathrm{Im}^2(s(t))}\\ \angle s(t) &= \mathrm{atan2}\left(\mathrm{Im}(s(t)), \mathrm{Re}(s(t)) \right) \end{aligned} \]

• WAR19 - Audio_Hilbert_WAR19.pdf
• Analytic signal - Wikipedia

Analytic Signal の計算

任意の信号 \(x\) は FFT を使って analytic signal \(s\) に変換できます。次の式は scipy.signal.hilbert の計算式で ステップ関数 \(U\) を使って負の周波数成分を0にしています。

\[ s = \mathtt{ifft}(\mathtt{fft}(x) 2 U) = x + j \mathcal{H}(x) \]

\(\mathcal{H}\) は ヒルベルト変換です。ヒルベルト変換された信号 \(\mathcal{H}(x)\) は、元の信号 \(x\) に比べると負の周波数成分の位相が90°進み、正の周波数成分の位相が90°遅れています。

FFT をリアルタイム処理で使うとレイテンシや計算コストが問題になることがあります。この問題を避けるためにオールパスフィルタを使って analytic signal を近似する方法があります。近似では2つのオールパスフィルタ \(H_{\mathrm{Re}},\,H_{\mathrm{Im}}\) を用意して、位相差 \(\angle (H_{\mathrm{Re}} / H_{\mathrm{Im}})\) がヒルベルト変換の位相特性を近似するようになっています。

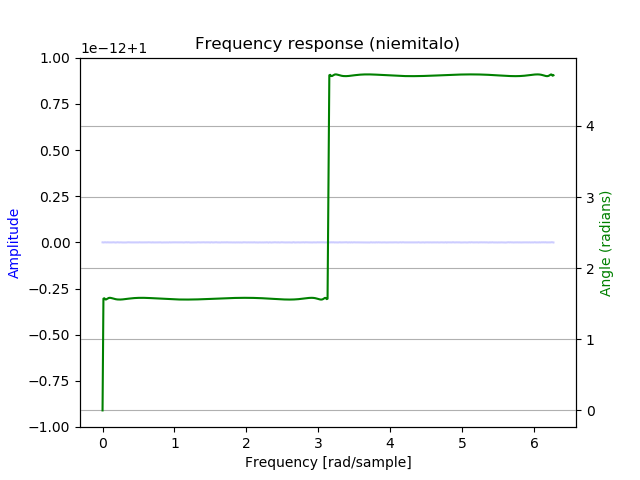
次の図は analytic signal の近似に使われる2つのオールパスフィルタの位相差です。

• scipy.signal.hilbert — SciPy v1.3.0 Reference Guide
• Hilbert transform - Wikipedia
• Analytic Signals and Hilbert Transform Filters | Mathematics of the DFT
• Analytic signal, Hilbert Transform and FFT – GaussianWaves

実装

コードはPython3です。次のライブラリを使っています。

• SciPy, NumPy
• PySoundfile

上から順番にコードをテキストファイルにコピペしていけば動くプログラムになっています。完成したコードは次のリンクから読むことができます。

• コードを読む

ヒルベルト変換

scipy.signal.hilbert を使います。

import numpy
import scipy.signal as signal

def frequency_shift(samplerate, analytic_signal, shift_hz):
    norm = numpy.abs(analytic_signal)
    theta = numpy.angle(analytic_signal)
    time = numpy.linspace(0, len(analytic_signal) / samplerate, len(analytic_signal))
    return norm * numpy.cos(theta + 2 * numpy.pi * shift_hz * time)

def naive(samplerate, sig, shift_hz=1000):
    return frequency_shift(samplerate, signal.hilbert(wav), shift_hz)

オールパスその1

Olli Niemitalo さんによって紹介されていたフィルタです。

式の \(\times\) は乗算です。横に長くなったので改行時に明示的に演算子を書いています。

\[ \begin{aligned} H_{sect}(z, a) =&\; \frac{a^2 - z^{-2}}{1 - a^2 z^{-2}}\\ H_{\mathrm{Re}}(z) =&\; H_{sect}(z, 0.4021921162426)\\ & \times H_{sect}(z, 0.8561710882420)\\ & \times H_{sect}(z, 0.9722909545651)\\ & \times H_{sect}(z, 0.9952884791278)\\ H_{\mathrm{Im}}(z) =&\; H_{sect}(z, 0.6923878)\\ & \times H_{sect}(z, 0.9360654322959)\\ & \times H_{sect}(z, 0.9882295226860)\\ & \times H_{sect}(z, 0.9987488452737)\\ & \times z^{-1}\\ H_{Hilbert}(z) =& 0.5 ( H_{\mathrm{Re}}(z) + j H_{\mathrm{Im}}(z)) \end{aligned} \]

def add_delay(sos):
    return numpy.vstack((sos, [0, 1, 0, 1, 0, 0]))

def olli(samplerate, sig, shift_hz=1000):
    def section(a):
        a2 = a * a
        return [a2, 0, -1, 1, 0, -a2]

    sos_real = numpy.array([
        section(a) for a in [
            0.4021921162426, 0.8561710882420,
            0.9722909545651, 0.9952884791278,
        ]
    ])
    sos_imag = numpy.array([
        section(a) for a in [
            0.6923878000000, 0.9360654322959,
            0.9882295226860, 0.9987488452737,
        ]
    ])
    sos_imag = add_delay(sos_imag)

    real = signal.sosfilt(sos_real, sig)
    imag = signal.sosfilt(sos_imag, sig)
    analytic = 0.5 * (real + 1j * imag)
    return frequency_shift(samplerate, analytic, shift_hz)

• Hilbert transform « iki.fi/o

オールパスその2

IIR Hilbert Transformer で Robby Wasabi さんによって紹介されていたフィルタです。

\[ \begin{aligned} H_{\mathrm{Re}}(z) =&\; \frac{0.190696 - z^{-2}}{1 - 0.190696 z^{-2}} \times \frac{0.860735 - z^{-2}}{1 - 0.860735 z^{-2}}\\ H_{\mathrm{Im}}(z) =&\; \frac{0.553100 - z^{-2}}{1 - 0.553100 z^{-2}} \times z^{-1}\\ H_{Hilbert}(z) =&\; 0.5 \left( H_{\mathrm{Re}}(z) + j H_{\mathrm{Im}}(z) \right) \end{aligned} \]

def wasabi(samplerate, sig, shift_hz=1000):
    sos_real = numpy.array([
        [0.190696, 0, -1, 1, 0, -0.190696],
        [0.860735, 0, -1, 1, 0, -0.860735],
    ])
    sos_imag = numpy.array([[0.553100, 0, -1, 1, 0, -0.553100]])
    sos_imag = add_delay(sos_imag)

    real = signal.sosfilt(sos_real, sig)
    imag = signal.sosfilt(sos_imag, sig)
    analytic = 0.5 * (real + 1j * imag)
    return frequency_shift(samplerate, analytic, shift_hz)

• transform - IIR Hilbert Transformer - Signal Processing Stack Exchange

オールパスその3

Pure Data の hilbert~ で使われているフィルタです。コメントで Emmanuel Favreau さんが 1982 年頃に作った 4X のパッチから取ってきた、とクレジットされています。

\[ \begin{aligned} H_{biquad}(z, a_1, a_2) =&\; \frac{a_2 + a_1 z^{-1} + z^{-2}}{1 + a_1 z^{-1} + a_2 z^{-2}}\\ H_{\mathrm{Re}}(z) =&\; H_{biquad}(z, 0.02569, -0.260502) H_{biquad}(z, -1.8685, 0.870686)\\ H_{\mathrm{Im}}(z) =&\; H_{biquad}(z, -1.94632, 0.94657) H_{biquad}(z, -0.83774, 0.06338)\\ H_{Hilbert}(z) =&\; H_{\mathrm{Re}}(z) + j H_{\mathrm{Im}}(z) \end{aligned} \]

def favreau(samplerate, sig, shift_hz=1000):
    def biquad(a1, a2):
        return [a2, a1, 1, 1, a1, a2]

    sos_real = numpy.array([
        biquad(0.02569, -0.260502),
        biquad(-1.8685, 0.870686),
    ])
    sos_imag = numpy.array([
        biquad(-1.94632, 0.94657),
        biquad(-0.83774, 0.06338),
    ])

    real = signal.sosfilt(sos_real, sig)
    imag = signal.sosfilt(sos_imag, sig)
    analytic = 0.5 * (real + 1j * imag)
    return frequency_shift(samplerate, analytic, shift_hz)

• pure-data/hilbert~.pd at master · pure-data/pure-data · GitHub
• OL-OWLPatches/IIRHilbert.lib at master · olilarkin/OL-OWLPatches · GitHub
• electro-music.com :: View topic - Hilbert transform code

オールパスその4

Signal Processing Stack Exchange で Ross Wilkinson さんが紹介していたフィルタです。

奇数の \(k\) についてフィルタの零点 \(q_n\) 、極 \(p_n\) を定義します。 \(n\) は整数です。

\[ \begin{aligned} q_n &= \begin{cases} \exp \left( \pi / 2^n \right) & \text{if} & n\geq 0,\\ -\exp \left( \pi / 2^{|n|} \right) & \text{if} & n < 0. \end{cases}\\ p_n &= \frac{1}{q_n}.\\ \quad n &\in [-k, k], \quad n \in \mathbb{Z}. \quad k\,\text{ is odd}. \end{aligned} \]

\(n\) が偶数のときだけを取り出したフィルタ \(A_k\) と、 \(n\) が奇数のときだけを取り出したフィルタ \(B_k\) の2つのフィルタを作ります。

\[ \begin{aligned} Q_n &= (q_n,\,p_n)\\ \hat{A}_k &= \begin{bmatrix} Q_{0}& Q_{2}& Q_{4}& \dots& Q_{k - 5}& Q_{k - 3}& Q_{k - 1} \end{bmatrix}\\ A_k &= \mathtt{concat}(-\hat{A}_k, \hat{A}_k)\\ \hat{B}_k &= \begin{bmatrix} Q_{1} & Q_{3} & Q_{5} & \dots & Q_{k - 4} & Q_{k - 2} & Q_{k} \end{bmatrix}\\ B_k &= \mathtt{concat}(-\hat{B}_k, \hat{B}_k)\\ \end{aligned} \]

\(A_k\) の伝達関数を \(H_{A_k}(z)\) 、 \(B_k\) の伝達関数を \(H_{B_k}(z)\) とすると analytic signal を次のように近似できます。

\[ H_{Hilbert}(z) = H_{A_k}(z) + j z^{-1} H_{B_k}(z) \]

def wilkinson(samplerate, sig, shift_hz=1000):
    k = 9
    n = numpy.arange((k + 1) / 2)

    zero_real = numpy.exp(numpy.pi / 2**(2 * n))
    zero_real = numpy.append(zero_real, -zero_real)

    zero_imag = numpy.exp(numpy.pi / 2**(2 * n + 1))
    zero_imag = numpy.append(zero_imag, -zero_imag)

    sos_real = signal.zpk2sos(zero_real, 1 / zero_real, 1e-5)
    sos_imag = signal.zpk2sos(zero_imag, 1 / zero_imag, 1e-5)
    sos_imag = add_delay(sos_imag)

    real = signal.sosfilt(sos_real, sig)
    imag = signal.sosfilt(sos_imag, sig)
    analytic = real - 1j * imag

    sig = frequency_shift(samplerate, analytic, shift_hz)
    peak = numpy.max(numpy.abs(sig))
    return sig / peak if peak != 0 else sig

• Hilbert transform filter for audio applications: Using IIR half-band parallel all pass structure - Signal Processing Stack Exchange

オールパスその5

Peter C. McNulty さんによって紹介されていたフィルタです。リンク先の Table 1 の抵抗の単位 [W] は \(\Omega\) (オーム) の意味です。 \(\Omega\) の文字が表示できないときは W で代用されることがあるそうです。

フィルタネットワークで使われるオールパスフィルタの伝達関数です。

\[ \begin{aligned} H_{AP}(s, R, C) =&\; \frac{-1 + 2\pi RCs}{1 + 2\pi RCs}\\ H_{\mathrm{Re}}(s) =&\; H_{AP}(s, 93100, 100p)\\ &\times H_{AP}(s, 90900, 470p)\\ &\times H_{AP}(s, 102000, 1800p)\\ &\times H_{AP}(s, 95300, 8200p)\\ &\times H_{AP}(s, 101000, 33000p)\\ &\times H_{AP}(s, 96500, 270000p)\\ H_{\mathrm{Im}}(s) =&\; H_{AP}(s, 98800, 27p)\\ &\times H_{AP}(s, 104000, 200p)\\ &\times H_{AP}(s, 88700, 1000p)\\ &\times H_{AP}(s, 97600, 3900p)\\ &\times H_{AP}(s, 107000, 15000p)\\ &\times H_{AP}(s, 109000, 68000p)\\ p =&\; 10^{-12}\\ H_{Hilbert}(s) =&\; H_{\mathrm{Re}}(s) - j H_{\mathrm{Im}}(s) \end{aligned} \]

\(H_{AP}\) は連続系なので scipy.signal.cont2discrete で離散系に変えます。 cont2discrete の method は zoh よりも gbt にしたほうがノイズが減りました。

from numpy.polynomial import polynomial

def allpass(samplerate, rc):
    rc *= 2 * numpy.pi
    num, den, dt = signal.cont2discrete(
        ([rc, -1], [rc, 1]), 1 / samplerate, "gbt", 0.5)
    return num[0], den

def mcnulty(samplerate, sig, shift_hz=1000):
    rc_real = [
        allpass(samplerate, rc) for rc in [
            9.31e-06, 4.2723e-05, 0.0001836,
            0.00078146, 0.003333, 0.026055
        ]
    ]
    rc_imag = [
        allpass(samplerate, rc) for rc in [
            2.6676e-06, 2.08e-05, 8.87e-05,
            0.00038064, 0.0016049999999999999, 0.007412,
        ]
    ]

    sos_real = [
        signal.tf2sos(
            polynomial.polymul(rc1[0], rc2[0]),
            polynomial.polymul(rc1[1], rc2[1]),
        )[0] for rc1, rc2 in zip(rc_real[::2], rc_real[1::2])
    ]
    sos_imag = [
        signal.tf2sos(
            polynomial.polymul(rc1[0], rc2[0]),
            polynomial.polymul(rc1[1], rc2[1]),
        )[0] for rc1, rc2 in zip(rc_imag[::2], rc_imag[1::2])
    ]

    real = signal.sosfilt(sos_real, sig)
    imag = signal.sosfilt(sos_imag, sig)

    analytic = 0.5 * (real - 1j * imag)
    return frequency_shift(samplerate, analytic, shift_hz)

• Analog Wide Band Audio Phase Shift Networks
• Ohm - Wikipedia

オールパスその6

これも McNulty さんによって紹介されていたフィルタです。設計は Chuck さんによるそうです。

\[ \begin{aligned} H_{AP}(s, R, C) =&\; \frac{-1 + 2\pi RCs}{1 + 2\pi RCs}\\ H_{\mathrm{Re}}(z) =&\; H_{AP}(z, 5490, 0.001\mu)\\ &\times H_{AP}(z, 47500, 0.001\mu)\\ &\times H_{AP}(z, 237000, 0.001\mu)\\ &\times H_{AP}(z, 127000, 0.01\mu)\\ H_{\mathrm{Im}}(z) =&\; H_{AP}(z, 20000, 0.001\mu)\\ &\times H_{AP}(z, 107000, 0.001\mu)\\ &\times H_{AP}(z, 536000, 0.001\mu)\\ &\times H_{AP}(z, 464000, 0.01\mu)\\ \mu =&\; 10^{-6}\\ H_{Hilbert}(s) =&\; H_{\mathrm{Re}}(s) - j H_{\mathrm{Im}}(s) \end{aligned} \]

def chuck(samplerate, sig, shift_hz=1000):
    rc_imag = [
        allpass(samplerate, rc)
        for rc in [5.49e-06, 4.75e-05, 2.37e-04, 1.27e-03]
    ]
    rc_real = [
        allpass(samplerate, rc)
        for rc in [2.00e-05, 1.07e-04, 5.36e-04, 4.64e-03]
    ]

    sos_imag = [
        signal.tf2sos(
            polynomial.polymul(rc1[0], rc2[0]),
            polynomial.polymul(rc1[1], rc2[1]),
        )[0] for rc1, rc2 in zip(rc_imag[::2], rc_imag[1::2])
    ]

    sos_real = [
        signal.tf2sos(
            polynomial.polymul(rc1[0], rc2[0]),
            polynomial.polymul(rc1[1], rc2[1]),
        )[0] for rc1, rc2 in zip(rc_real[::2], rc_real[1::2])
    ]

    real = signal.sosfilt(sos_real, sig)
    imag = signal.sosfilt(sos_imag, sig)

    analytic = 0.5 * (real - 1j * imag)
    return frequency_shift(samplerate, analytic, shift_hz)

• Analog Wide Band Audio Phase Shift Networks

音のサンプル

次のようなコードで音をレンダリングしました。

import soundfile

data, samplerate = soundfile.read("snd/yey.wav", always_2d=True)
wav = data.T[0]
shift_hz = 200  # Hz

out = naive(samplerate, wav, shift_hz)
soundfile.write("naive.wav", out, samplerate)

\(\omega_c = 1000\) として周波数シフトした音のサンプルです。ソースは freesound.org で見つけた hemogREC さんによる yey.wav です。

Wilkinson のフィルタは特性は問題ないのですが、うまく周波数シフトできていません。直列2次セクションに変換するときに何か問題があるのかもしれません。 Wasabi のフィルタもノイズがはっきりと聞き取れます。

その他

周波数特性の位相差

伝達関数の周波数特性は複素数で表されているので、位相差の計算 \(\angle (H_{\mathrm{Re}} / H_{\mathrm{Im}})\) では除算が出てきます。複素数の除算は次のように書けます。

\[ \frac{z_1}{z_2} = \frac{r_1}{r_2} e^{j (\phi_1 - \phi_2)},\quad z_1 = r_1 e^{j \phi_1},\quad z_2 = r_2 e^{j \phi_2} \]

よって \(\angle (z_1 / z_2)\) は \(\phi_1 - \phi_2\) です。

scipy.signal の sos

scipy.signal で sos と略されている cascaded second-order sections のデータ構造です。

sos = [
  [b00, b01, b02, 1, a01, a02],
  [b10, b11, b12, 1, a11, a12],
  [b20, b21, b22, 1, a21, a22],
  ...
]

伝達関数は次のようになります。

\[ H(z) = \frac{b_{00} + b_{01} z^{-1} + b_{02} z^{-2}} {1 + a_{01} z^{-1} + a_{02} z^{-2}} \times \frac{b_{10} + b_{11} z^{-1} + b_{12} z^{-2}} {1 + a_{11} z^{-1} + a_{12} z^{-2}} \times \frac{b_{20} + b_{21} z^{-1} + b_{22} z^{-2}} {1 + a_{21} z^{-1} + a_{22} z^{-2}} \times \dots \]

Pure Data の biquad~

Pure Data の biquad~ の係数を移植するときは fb の符号を逆にしないと正しく動かないことがあります。

biquad~ の引数です。

"biquad~" [fb1] [fb2] [ff1] [ff2] [ff3]

biquad~ の伝達関数です。

\[ H(z) = \frac{ \mathtt{ff_1} + \mathtt{ff_2} z^{-1} + \mathtt{ff_3} z^{-2} }{ 1 - \mathtt{fb_1} z^{-1} - \mathtt{fb_2} z^{-2} } \]

scipy.signal に移植するときは次のように書けます。

sos_biquad = [[ff1, ff2, ff3, 1, -fb1, -fb2]]
output = scipy.signal.sosfilt(sos_biquad, some_signal)

• Programming Electronic Music in Pd - 3.3 Subtractive synthesis

ピッチシフトと周波数シフト

full bucket music の Frequency Shifter の説明文によるとピッチシフトと周波数シフトとは別物です。ピッチシフトは倍音構造が保持されますが、周波数シフトは倍音構造が崩れてしまうからです。

この記事はもともと AM ピッチシフトという呼び方を使っていましたが、今は AM 周波数シフトという呼び方に変更しました。 URL が am_pitchshift.html となっているのはその名残です。

変更点

• 2024/02/16
  • タイトルの「AM変調」を「AM」に変更。
  • コードの pitch_shift を frequency_shift に変更。
• 2022/05/08
  • 手法の呼び方を AM ピッチシフトから AM 周波数シフトに変更。
• 2019/08/06
  • コードの shift_hz が誤って周波数のまま扱われていた部分を角周波数に修正。